Skip to main content

Advertisement

SpringerLink
Log in

Numerical optimization of coordinated reset stimulation for desynchronizing neuronal network dynamics

  • Published:
Journal of Computational Neuroscience Aims and scope Submit manuscript

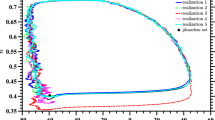
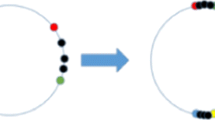
Abstract

Excessive synchronization in neural activity is a hallmark of Parkinson’s disease (PD). A promising technique for treating PD is coordinated reset (CR) neuromodulation in which a neural population is desynchronized by the delivery of spatially-distributed current stimuli using multiple electrodes. In this study, we perform numerical optimization to find the energy-optimal current waveform for desynchronizing neuronal network with CR stimulation, by proposing and applying a new optimization method based on the direct search algorithm. In the proposed optimization method, the stimulating current is described as a Fourier series, and each Fourier coefficient as well as the stimulation period are directly optimized by evaluating the order parameter, which quantifies the synchrony level, from network simulation. This direct optimization scheme has an advantage that arbitrary changes in the dynamical properties of the network can be taken into account in the search process. By harnessing this advantage, we demonstrate the significant influence of externally applied oscillatory inputs and non-random network topology on the efficacy of CR modulation. Our results suggest that the effectiveness of brain stimulation for desynchronization may depend on various factors modulating the dynamics of the target network. We also discuss the possible relevance of the results to the efficacy of the stimulation in PD treatment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Adamchic, I., Hauptmann, C., Barnikol, U. B., Pawelczyk, N., Popovych, O., Barnikol, T. T., Silchenko, A., Volkmann, J., Deuschl, G., Meissner, W. G., Maarouf, M., Sturm, V., Freund, H. J., & Tass, P. A. (2014). Coordinated reset neuromodulation for Parkinson’s disease: Proof-of-concept study. Movement Disorders, 29, 1679–1684.

    Article  PubMed  PubMed Central  Google Scholar 

  • Baizabal-Carvallo, J. F., Kagnoff, M. N., Jimenez-Shahed, J., Fekete, R., & Jankovic, J. (2014). The safety and efficacy of thalamic deep brain stimulation in essential tremor: 10 years and beyond. Journal of Neurology Neurosurgery and Psychiatry, 85, 567–572.

    Article  Google Scholar 

  • Barahona, M., & Pecora, L. M. (2002). Synchronization in small-world systems. Physical Review Letters, 89, 054101.

    Article  PubMed  CAS  Google Scholar 

  • Benabid, A. L., Chabardes, S., Mitrofanis, J., & Pallak, P. (2009). Deep brain stimulation of the subthalamic nucleus for the treatment of Parkinson’s disease. The Lancet Neurology, 8, 67–81.

    Article  PubMed  Google Scholar 

  • Bettencourt, L. M. A., Stephens, G. J., Ham, M. I., & Gross, G. W. (2007). Functional structure of cortical neuronal networks grown in vitro. Physical Review E, 75, 021915.

    Article  CAS  Google Scholar 

  • Brocker, D. T., Swan, B. D., So, R. Q., Turner, D. A., Gross, R. E., & Grill, W. M. (2017). Optimized temporal pattern of brain stimulation designed by computational evolution. Science Translational Medicine, 9, eaah3532.

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  • Cogan, S. F. (2008). Neural stimulation and recording electrodes. Annual Reviews of Biomedical Engineering, 10, 275–309.

    Article  CAS  Google Scholar 

  • Cogan, S. F., Troyk, P. R., Ehrlich, J., Plante, T. D., & Detlefsen, D. E. (2006). Potential-biased, asymmetric waveforms for charge-injection with activated iridium oxide (AIROF) neural stimulation electrodes. IEEE Transactions on Biomedical Engineering, 53, 327–332.

    Article  PubMed  Google Scholar 

  • Dixon, L. C. W. (1972). Nonlinear optimization. London: The English Universities Press.

    Google Scholar 

  • Dovzhenok, A., & Rubchinsky, L. L. (2012). On the origin of tremor in Parkinson’s disease. PLoS One, 7, e41598.

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  • Drouot, X., Oschino, S., Jarraya, B., Besret, L., Kishima, H., Remy, P., Dauguet, J., Lefaucheur, J. P., Dolle, F., Conde, F., Bottlaender, M., Peschanski, M., Keravel, Y., Hantraye, P., & Palfi, S. (2004). Functional recovery in a primate model of Parkinson’s disease following motor cortex stimulation. Neuron, 44, 769–778.

    Article  PubMed  CAS  Google Scholar 

  • Ebert, M., Hauptmann, C., & Tass, P. A. (2014). Coordinated reset stimulation in a large-scale model of the STN-GPe circuit. Frontiers in Computational Neuroscience, 8, 154.

    Article  PubMed  PubMed Central  Google Scholar 

  • Fan, D., Wang, Z., & Wang, Q. (2016). Optimal control of directional deep brain stimulation in the parkinsonian neuronal network. Communications in Nonlinear Science and Numerical Simulation, 36, 219–237.

    Article  Google Scholar 

  • Feng, J., Brown, D., & Li, G. (2000). Synchronization due to common pulsed input in Stein’s model. Physical Review E, 61, 2987–2995.

    Article  CAS  Google Scholar 

  • Feng, X. J., Greenwald, B., Rabitz, H., Shea-Brown, E., & Kosut, R. (2007). Toward closed-loop optimization of deep brain stimulation for Parkinson’s disease: concepts and lessons from a computational model. Journal of Neural Engineering, 4(2), L14–L21.

    Article  PubMed  Google Scholar 

  • Forger, D. B., Paydarfar, D., & Clay, J. R. (2011). Optimal stimulus shapes for neuronal excitation. PLoS Computational Biology, 7, e1002089.

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  • Foutz, T. J., & McIntyre, C. C. (2010). Evaluation of novel stimulus waveforms for deep brain stimulation. Journal of Neural Engineering, 7, 066008.

    Article  PubMed  PubMed Central  Google Scholar 

  • Gatev, P., Darbin, O., & Wichmann, T. (2006). Oscillations in the basal ganglia under normal conditions and in movement disorders. Movement Disorders, 21, 1566–1677.

    Article  PubMed  Google Scholar 

  • Gaynor, L. M. F. D., Kühn, A. A., Dileone, M., Litvak, V., Eusebio, A., Pogosyan, A., Androulidakis, A. G., Tisch, S., Limousin, P., & Insola, A. (2008). Suppression of beta oscillations in the subthalamic nucleus following cortical stimulation in humans. European Journal of Neuroscience, 28, 1686–1695.

    Article  PubMed  Google Scholar 

  • Gerhard, F., Pipa, G., Lima, B., Neuenschwander, S., & Gerstner, W. (2011). Extraction of network topology from multi-electrode recordings: is there a small-world effect? Frontiers in Computational Neuroscience, 5, 4.

    Article  PubMed  PubMed Central  Google Scholar 

  • Greenwald, E., Masters, M. R., & Thakor, N. V. (2016). Implantable neurotechnologies: bidirectional neural interfaces–applications and VLSI circuit implementations. Medical and Biological Engineering and Computing, 54, 1–17.

    Article  PubMed  Google Scholar 

  • Grill, W. M. (2015). Model-based analysis and design of waveforms for efficient neural stimulation. Progress in Brain Research, 222, 147–162.

    Article  PubMed  PubMed Central  Google Scholar 

  • Guo, Y., & Rubin, J. E. (2011). Multi-site stimulation of subthalamic nucleus diminishes thalamocortical relay errors in a biophysical network model. Neural Networks, 24(6), 602–616.

    Article  PubMed  Google Scholar 

  • Haeusler, S., & Maass, W. (2007). A statistical analysis of information-processing properties of lamina-specific cortical microcircuit models. Cerebral Cortex, 17, 149–162.

    Article  PubMed  Google Scholar 

  • Herrington, T. M., Cheng, J. J., & Eskandar, E. N. (2016). Mechanisms of deep brain stimulation. Journal of Neurophysiology, 115, 19–38.

    Article  PubMed  CAS  Google Scholar 

  • Hofmann, L., Ebert, M., Tass, P. A., & Hauptmann, C. (2011). Modified pulse shapes for effective neural stimulation. Frontiers in Neuroengineering, 4, 9.

    Article  PubMed  PubMed Central  Google Scholar 

  • Hong, H., Choi, M. Y., & Kim, B. J. (2002). Synchronization on small-world networks. Physical Review E, 65, 026139.

    Article  CAS  Google Scholar 

  • Hooke, R., & Jeeves, T. A. (1961). Direct search solution of numerical and statistical problems. Journal of Association of Computing Machinery, 8, 212–229.

    Article  Google Scholar 

  • Izhikevich, E. M., Gally, J. A., & Edelman, G. M. (2004). Spike-timing dynamics of neuronal groups. Cerebral Cortex, 14, 933–944.

    Article  PubMed  Google Scholar 

  • Jezernik, S., & Morari, M. (2005). Energy-optimal electrical excitation of nerve fibers. IEEE Transactions on Biomedical Engineering, 52, 740–743.

    Article  PubMed  Google Scholar 

  • Jezernik, S., Sinkjaer, T., & Morari, M. (2010). Charge and energy minimization in electrical/magnetic stimulation of nervous tissue. Journal of Neural Engineering, 7, 046004.

    Article  PubMed  Google Scholar 

  • Khambampati, A. K., Ijaz, U. Z., Lee, J. S., Kim, S., & Kim, K. Y. (2010). Phase boundary estimation in electrical impedance tomography using the Hooke and Jeeves pattern search method. Measurement Science and Technology, 21, 035501.

    Article  CAS  Google Scholar 

  • Kubota, S., Kanomata, K., Suzuki, T., Ahmmad, B., & Hirose, F. (2015). Hybrid antireflection structure with moth eye and multilayer coating for organic photovoltaics. Journal of Coatings Technology and Research, 12, 37–47.

    Article  CAS  Google Scholar 

  • Kühn, A. A., & Volkmann, J. (2017). Innovations in deep brain stimulation methodology. Movement Disorders, 32, 11–19.

    Article  PubMed  Google Scholar 

  • Kühn, A. A., Kempf, F., Brücke, C., Doyle, L. G., Martinez-Torres, I., Pogosyan, A., Trottenberg, T., Kupsch, A., Schneider, G. H., Hariz, M. I., Vandenberghe, W., Nuttin, B., & Brown, P. (2008). High-frequency stimulation of the subthalamic nucleus suppresses oscillatory β activity in patients with Parkinson's disease in parallel with improvement in motor performance. Journal of Neuroscience, 28(24), 6165–6173.

    Article  PubMed  CAS  Google Scholar 

  • Kumar, R., Lozano, A. M., Sime, E., & Lang, A. E. (2003). Long-term follow-up of thalamic deep brain stimulation for essential and parkinsonian tremor. Neurology, 61, 1601–1604.

    Article  PubMed  Google Scholar 

  • Kuncel, A. M., & Grill, W. M. (2004). Selection of stimulus parameters for deep brain stimulation. Clinical Neurophysiology, 115, 2431–2441.

    Article  PubMed  Google Scholar 

  • Lavano, A., Guzzi, G., De Rose, M., Romano, M., Della Torre, A., Vescio, G., Deodato, F., Lavano, F., & Volpentesta, G. (2017). Minimally invasive motor cortex stimulation for Parkinson’s disease. Journal of Neurosurgical Sciences, 61, 77–87.

    PubMed  Google Scholar 

  • Liu, Y. H., & Wang, X. J. (2001). Spike-frequency adaptation of a generalized leaky integrate-and-fire model neuron. Journal of Computational Neuroscience, 10, 25–45.

    Article  PubMed  CAS  Google Scholar 

  • Mallet, N., Pogosyan, A., Sharott, A., Csicsvari, J., Bolam, J. P., Brown, P., & Magill, P. J. (2008). Disrupted dopamine transmission and the emergence of exaggerated beta oscillations in subthalamic nucleus and cerebral cortex. Journal of Neuroscience, 28, 4795–4806.

    Article  PubMed  CAS  Google Scholar 

  • Muthuraman, M., Deuschl, G., Koirala, N., Riedel, C., Volkmann, J., & Groppa, S. (2017). Effects of DBS in parkinsonian patients depend on the structural integrity of frontal cortex. Scientific Reports, 7, 43571.

    Article  PubMed  PubMed Central  Google Scholar 

  • Ondo, W., Jankovic, J., Schwartz, K., Almaguer, M., & Simpson, R. K. (1998). Unilateral thalamic deep brain stimulation for refractory essential tremor and Parkinson’s disease tremor. Neurology, 51, 1063–1069.

    Article  PubMed  CAS  Google Scholar 

  • Prettejohn, B. J., Berryman, M. J., & McDonnell, M. D. (2011). Methods for generating complex networks with selected structural properties for simulations: A review and tutorial for neuroscientists. Frontiers in Computational Neuroscience, 5, 11.

    Article  PubMed  PubMed Central  Google Scholar 

  • Reich, M. M., Steigerwald, F., Sawalhe, A. D., Reese, R., Gunalan, K., Johannes, S., Nickl, R., Matthies, C., McIntyre, C. C., & Volkmann, J. (2015). Short pulse width widens the therapeutic window of subthalamic neurostimulation. Annals of Clinical and Tranlational Neurology, 2, 427–432.

    Article  Google Scholar 

  • Rosin, B., Slovik, M., Mitelman, R., Rivlin-Etzion, M., Haber, S. N., Israel, Z., Vaadia, E., & Bergman, H. (2011). Closed-loop deep brain stimulation is superior in ameliorating parkinsonism. Neuron, 72, 370–384.

    Article  PubMed  CAS  Google Scholar 

  • Rubin, J. E., & Terman, D. (2004). High frequency stimulation of the subthalamic nucleus eliminates pathological thalamic rhythmicity in a computational model. Journal of Computational Neuroscience, 16(3), 211–235.

    Article  PubMed  Google Scholar 

  • Rubin, J. E., McIntyre, C. C., Turner, R. S., & Wichmann, T. (2012). Basal ganglia activity patterns in parkinsonism and computational modeling of their downstream effects. European Journal of Neuroscience, 36, 2213–2228.

    Article  PubMed  Google Scholar 

  • Sahin, M., & Tie, Y. (2007). Non-rectangular waveforms for neural stimulation with practical electrodes. Journal of Neural Engineering, 4, 227–233.

    Article  PubMed  PubMed Central  Google Scholar 

  • Santaniello, S., McCarthy, M. M., Montgomery, E. B., Gale, J. T., Kopell, N., & Sarma, S. V. (2015). Therapeutic mechanisms of high-frequency stimulation in Parkinson’s disease and neural restoration via loop-based reinforcement. Proceedings of the National Academy of Sciences of the United States of America, 112, E586–E595.

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  • Tass, P. A. (2003). A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biological Cybernetics, 89, 81–88.

    Article  PubMed  Google Scholar 

  • Tass, P. A., Qin, L., Hauptmann, C., Dovero, S., Bezard, E., Boraud, T., & Meissner, W. G. (2012). Coordinated reset has sustained aftereffects in Parkinsonian monkeys. Annals of Neurology, 72, 816–820.

    Article  PubMed  Google Scholar 

  • Terman, D., Rubin, J. E., Yew, A. C., & Wilson, C. J. (2002). Activity patterns in a model for the subthalamopallidal network of the basal ganglia. Journal of Neuroscience, 22, 2963–2976.

    Article  PubMed  CAS  Google Scholar 

  • Troyer, T. W., & Miller, K. D. (1997). Physiological gain leads to high ISI variability in a simple model of a cortical regular spiking cell. Neural Computation, 9, 971–983.

    Article  PubMed  CAS  Google Scholar 

  • Türker, K. S., & Powers, R. K. (2001). Effects of common excitatory and inhibitory inputs on motoneuron synchronization. Journal of Neurophysiology, 86, 2807–2822.

    Article  PubMed  Google Scholar 

  • Wang, J., Nebeck, S., Muralidharan, A., Johnson, M. D., Vitek, J. L., & Baker, K. B. (2016). Coordinated reset deep brain stimulation of subthalamic nucleus produces long-lasting, dose-dependent motor improvements in the 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine non-human primate model of parkinsonism. Brain Stimulation, 9, 609–617.

    Article  PubMed  Google Scholar 

  • Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393, 440–442.

    Article  PubMed  CAS  Google Scholar 

  • Wilson, D., & Moehlis, J. (2014a). Locally optimal extracellular stimulation for chaotic desynchronization of neural populations. Journal of Computational Neuroscience, 37, 243–257.

    Article  PubMed  PubMed Central  Google Scholar 

  • Wilson, D., & Moehlis, J. (2014b). Optimal chaotic desynchronization for neural populations. SIAM Journal on Applied Dynamical Systems, 13, 276–305.

    Article  Google Scholar 

  • Wise, K. D., Sodagar, A. M., Yao, Y., Gulari, M. N., Perlin, G. E., & Najafi, K. (2008). Microelectrodes, microelectronics, and implantable neural microsystems. Proceedings of the IEEE, 96, 1184–1202.

    Article  CAS  Google Scholar 

  • Wongsarnpigoon, A., & Grill, W. M. (2010). Energy-efficient waveform shapes for neural stimulation revealed with genetic algorithm. Journal of Neural Engineering, 7, 046009.

    Article  PubMed  PubMed Central  Google Scholar 

  • Wongsarnpigoon, A., Woock, J. P., & Grill, W. M. (2010). Efficiency analysis of waveform shape for electrical excitation of nerve fibers. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 18, 319–328.

    Article  PubMed  PubMed Central  Google Scholar 

  • Yu, S., Huang, D., Singer, W., & Nikolic, D. (2008). A small world of neuronal synchrony. Cerebral Cortex, 18, 2891–2901.

    Article  PubMed  Google Scholar 

Download references

Acknowledgements

JR received support from US National Science Foundation awards DMS 1516288 and DMS 1612913.

Author information

Authors and Affiliations

  1. Graduate School of Science and Engineering, Yamagata University, 4-3-16 Jonan, Yonezawa, Yamagata, 992-8510, Japan

    Shigeru Kubota

  2. Department of Mathematics, University of Pittsburgh, 301 Thackeray Hall, Pittsburgh, PA, 15260, USA

    Jonathan E. Rubin

Authors
  1. Shigeru Kubota
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jonathan E. Rubin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shigeru Kubota.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Action Editor: Charles Wilson

Electronic supplementary material

Figure S1

Comparison of the energy efficiency of the asymmetric pulse input with that of the symmetric pulse and Fourier inputs. (a) An example of the current waveform of the asymmetric pulse, which is optimized with the weight parameter α = 3.1 nA−2·mS. Each current is delivered by the electrode represented using the same color in Fig. 1(a). (b) The red lines show the values of E (solid) and ρ (dashed) as function of α, obtained by using the optimal asymmetric pulse. The black lines show the case of using the optimal symmetric pulse (the same as shown in Fig. 3b), for comparison. (c) The red line shows the relationship between ρ and E obtained by applying the asymmetric pulse which is optimized with various α values. The black lines represent the cases with the optimal Fourier (solid) and symmetric pulse (dashed) (the same as shown in Fig. 3c), for comparison. (EPS 1589 kb)

High resolution image (PNG 63 kb)

Figure S2

The predicted effects of applying intermittent stimulus control in which the current stimulation is periodically switched on and off. (a and b) Examples of the time courses of order parameter r (top) and one of the four stimulating currents (\( {I}_{stim}^j \) in Eq. (4)) (bottom), when the intermittent control is applied to the Fourier (a) and symmetric pulse (b) inputs. The stimulus waveform is optimized in the absence of intermittent regulation with the weight parameter α = 3.1 nA−2·mS. The dashed vertical lines show the onset and end of the time period for activating stimulation. (c) The relationship between the average order parameter ρ and the energy consumption rate E obtained in the presence (red) and absence (black) of intermittent regulation for the inputs optimized with various α values. The intermittent control is applied to the Fourier (solid) and symmetric pulse (dashed) inputs, which are optimized without this control. In (a)-(c), the time durations of the active and inactive phases for the intermittent regulation are 1000 and 100 ms, respectively. (EPS 2038 kb)

High resolution image (PNG 65 kb)

Movie 1

Network activity in the absence of current stimulation, obtained with the same condition as in Fig. 4a. The colors of the circles and boxes represent the levels of the membrane potentials of neurons and the currents delivered by the electrodes, respectively. (MP4 2601 kb)

Movie 2

Network activity for the case of applying the optimal Fourier input with moderate intensity, obtained with the same condition as in Fig. 4b. (The meanings of the colors of the circles and boxes are the same as Movie 1.) (MP4 2608 kb)

Movie 3

Network activity for the case of applying the optimal Fourier input with strong intensity, obtained with the same condition as in Fig. 4c. (The meanings of the colors of the circles and boxes are the same as Movie 1.) (MP4 2597 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kubota, S., Rubin, J.E. Numerical optimization of coordinated reset stimulation for desynchronizing neuronal network dynamics. J Comput Neurosci 45, 45–58 (2018). https://doi.org/10.1007/s10827-018-0690-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10827-018-0690-z

Keywords

Search

Navigation