A calcium-influx-dependent plasticity model exhibiting multiple STDP curves

Abstract

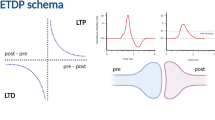
Hebbian plasticity means that if the firing of two neurons is correlated, then their connection is strengthened. Conversely, uncorrelated firing causes a decrease in synaptic strength. Spike-timing-dependent plasticity (STDP) represents one instantiation of Hebbian plasticity. Under STDP, synaptic changes depend on the relative timing of the pre- and post-synaptic firing. By inducing pre- and post-synaptic firing at different relative times the STDP curves of many neurons have been determined, and it has been found that there are different curves for different neuron types or synaptic sites. Biophysically, strengthening (long-term potentiation, LTP) or weakening (long-term depression, LTD) of glutamatergic synapses depends on the post-synaptic influx of calcium (Ca²⁺): weak influx leads to LTD, while strong, transient influx causes LTP. The voltage-dependent NMDA receptors are the main source of Ca²⁺ influx, but they will only open if a post-synaptic depolarisation coincides with pre-synaptic neurotransmitter release. Here we present a computational mechanism for Ca²⁺-dependent plasticity in which the interplay between the pre-synaptic neurotransmitter release and the post-synaptic membrane potential leads to distinct Ca²⁺ time-courses, which in turn lead to the change in synaptic strength. It is shown that the model complies with classic STDP results, as well as with results obtained with triplets of spikes. Furthermore, the model is capable of displaying different shapes of STDP curves, as observed in different experimental studies.

Appendices

Appendix A: Table of parameters & values used

Table 2 Parameters and their values used in the simulations used to make the figures in the main text

Appendix B: Comparison of saturated and unsaturated equations

In this appendix the effects of adding or removing certain saturations of the proposed models are investigated. As visible in Figs. 11 and 12 the removal of the saturations of Eq. (9) and (12), respectively, does not affect the results in a qualitative manner. The absolute values of the resulting A_f and A_s signals differ, but the relative values between the different spike timings stay preserved as in the case of the main text (Fig. 10).

Fig. 10

Standard model, using the equations as stated in the main text

Fig. 11

Model with added saturation for [Ca²⁺]. Parameters used: φ_f = 2e − 5; φ_s = 0.1; α_s = 1.73e − 5

Fig. 12

Model with added saturation for A_s. Parameters used: φ_f = 1e − 5; φ_s = 0.05; α_s = 9.5e − 6

However removing the saturation in Eq. (13) leads to qualitatively different results, as shown in Fig. 13a. After inspection it was found that the main difference between the saturised and un-saturised model are the maximal and mean levels reached by the A_f signal for different relative spike timings. Figure 13b shows the maximal levels of the A_f signal for different spike timings and shows that the un-saturised model (grey line) has highter maximal values especially for large spiking intervals than the saturised model (black line). The values of the normalised mean A_f values, as shown in Fig. 13c, show that in the saturised model (black line) the basic shape of the STDP window is shown by the mean A_f values, whereas the un-saturised model (grey line) shows a very different shape.

Fig. 13

Model with saturation removed for A_f. Same parameters as in main text

Appendix C: Equivalence of NMDA receptor product and difference of exponentials models

In the main text the variable governing the open-probability of the post-synaptic NMDA receptors is modelled as a product of a slow and a fast variable (see Eqs. (5) & (6)). More conventionally, a difference of exponentials is used to model the NMDA receptor open probability, which is fitted to follow the opening probability of kinetic synaptic transmission models as proposed by Destexhe et al. (1994a, b, 1998). The difference of exponentials, as used by Dayan and Abbott (2001), is given as:

$$ P_{s} = P_{max} B \left( e^{-t/\tau_{1}}-e^{-t/\tau_{2}} \right) $$

(14)

in which B is a normalising factor and τ₁ > τ₂ are time constants. The rise time of the variable P_s is given by: $\tau _{rise} = \frac {\tau _{1} \tau _{2}}{\tau _{1} - \tau _{2}}$ and the decay time is given by τ₁.

The variable used in this article is the product of a slow and a fast variable P_nmda = P⁺P⁻. P⁺ and P⁻ are governed by the differential equations (5) and (6), respectively. Integrating these equations, assuming a pre-synaptic pulse at time t = 0 gives:

$$ \begin{array}{@{}rcl@{}} P^{+} = 1-e^{-t/\tau^{+}}\text{ and }& P^{-} = e^{-t/\tau^{-}} \end{array} $$

(15)

Leading to:

$$ \begin{array}{@{}rcl@{}} P &=& P^{-}P^{+}= e^{-t/\tau^{-}} (1-e^{-t/\tau^{+}}) \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} &=& e^{-t/\tau^{-}} - e^{-t/\tau^{-}}e^{-t/\tau^{+}} \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} &=& e^{-t/\tau^{-}} - e^{-\frac{\tau^{-}+\tau^{+}}{\tau^{-}\tau^{+}}t} \end{array} $$

(18)

Then, by using the parameters from the main text (τ⁺ = 1.5ms and τ⁻ = 152ms), one finds that the decay time of the difference of exponentials is τ₁ = τ⁻ = 152ms, and the rise time τ_rise ≈ 1.5ms. Thus it is shown that the product of a slow and fast variable and the difference of exponentials models for synaptic opening are equivalent in this case. Figure 14 compares the results of a numerical simulation of the kinetic scheme for the NMDA synaptic transmission, as described in Destexhe et al. (1998), with the model for P_nmda used in this manuscript (Eqs. (5) and (6)).

Fig. 14

Comparison of the numerical simulation of the kinetic model for NMDA synaptic transmission (black line) and the synaptic transmission model used in the proposed model (grey line) for a single pulse of neurotransmitter at t = 100ms

Appendix D: Comparison of NMDA receptor opening simulations

In the presented model the NMDA recptor opening g_nmda (4) is goverened by the NMDA receptor open probability P_nmda (Eqs. (5) and (6)), which is related to the binding of glutamate to the receptor, and the Mg²⁺ unblocking $\widetilde {G}$, which is modelled as a low-passed version of the direct Mg²⁺ unblocking as given by Eq. (7) (Jahr and Stevens 1990; Dayan and Abbott 2001). Using a low-passed version of the Mg²⁺ unblocking is motivated by the observation that the unblock is not instantaneous (Vargas-Caballero and Robinson 2003; Kampa et al. 2004) and that the specific channel sub-unit make-up can alter the Mg²⁺ unblocking time-course (Vargas-Caballero and Robinson 2003; Qian et al. 2005; Clarke and Johnson 2006). In their paper, Kampa et al. (2004) provide a kinetic model that captures the non-instantaneous effect of the Mg²⁺ unblocking as they find in their data. This appendix provides a comparison between the kinetic model and Eqs. (4) through (8).

Simulations of both the kinetic model of Kampa et al. (2004) and Eqs. (4)–(8) have been done using one pre-post and one post-pre spike pairing, the same as during one run on the STDP induction protocol, with an inter-spike interval of 10ms. Figure 15 shows the resulting NMDA receptor opening following a pre-post pairing, Fig. 16 shows the NMDA receptor opening following a post-pre pairing. The black lines show the NMDA receptor opening as predicted by the Kampa et al. (2004) kinetic model, the NMDA receptor opening used in this paper is given by the grey lines. The P_nmda rise and fall time constants of Eqs. (5) and (6), respectively, have been altered in order to obtain a better fit with the kineticmodel (τ⁺ = 2ms, τ⁻ = 105ms).

Fig. 15

Comparison of the kinetic model of NMDA receptor opening (black line) and the NMDA receptor opening used in the current paper (grey line) for a single pre-post pairing (t_pre − t_post = − 10ms). In this simulation τ⁺ = 2ms (5) and τ⁻ = 105ms (6). Pre-synaptic timing (glutamate release) is indicated by the vertical line. Post-synaptic activity occurs at the arrow

Fig. 16

Comparison of the kinetic model of NMDA receptor opening (black line) and the NMDA receptor opening used in the current paper (solid line) for a single post-pre pairing (t_pre − t_post = 10ms). In this simulation τ⁺ = 2ms (5) and τ⁻ = 105ms (6). Pre-synaptic timing (glutamate release) is indicated by the vertical line. Post-synaptic activity occurs at the arrow

The results show large agreement in NMDA receptor opening between the kinetic model and Eqs. (4)–(8). The opening time-courses in the pre-post spike pairing case, shown in Fig. 15, show that the model used in this paper follows a decay time-course with a slight change in the decay rate around t ≈ 120ms in Fig. 15, due to the different interacting terms that lead to the NMDA receptor opening. However the two methods are in agreement on the large-scale shape and magnitude of the NMDA receptor opening. Figure 16 shows the results of both methods following a post-pre spike pairing. The peak magnitude of the NMDA receptor opening given by Eqs. (4)–(8) is slightly lower than that of the kinetic model, however, the models agree on the large scale shape of the NMDA receptor opening time-course.