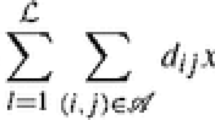Abstract
Vehicle routing problem is concerned with finding optimal collection or delivery routes in a transportation network, beginning and ending at a central depot, for a fleet of vehicles to serve a set of customers under some constraints. Assuming the travel times between two customers are uncertain variables, this paper proposes an uncertain multilevel programming model for a vehicle routing problem, of which the leader’s object is to minimize the total waiting times of the customers, and the followers’ objects are to minimize the waiting times of the vehicles for the beginning moments of the customers’ time windows. The uncertain multilevel programming model is transformed into a determinacy programming model, and an intelligent algorithm is designed for solving the crisp model.
Similar content being viewed by others
References
Chen, X., & Ralescu, D. A. (2013). Liu process and uncertain calculus. Journal of Uncertainty Analysis and Applications, 1, Article 3.
Clarke, C., & Wright, J. W. (1964). Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 12, 568–581.
Dantzig, G. B., & Ramser, J. H. (1959). The truck dispatching problem. Management Science, 6, 80–91.
Dong, G., Tang, J., Lai, K. K., & Kong, Y. (2011). An exact algorithm for vehicle routing and scheduling problem of free pickup and delivery service in flight ticket sales companies based on set-partitioning model. Journal of Intelligent Manufacturing, 22(5), 789–799.
Dror, M., Laporte, G., & Trudreau, P. (1989). Vehicle routing with stochastic demands: Properties and solution frameworks. Transportation Science, 23, 166–176.
Gao, Y. (2011). Shortest path problem with uncertain arc lengths. Computers and Mathematics with Applications, 62(6), 2591–2600.
Gen, M., & Cheng, R. (2000). Genetic algorithms and engineering optimization. New York: Wiley.
Gendreau, M., Laporte, G., & Séguin, R. (1995). An exact algorithm for the vehicle routing problem with stochastic customers and demands. Transportation Science, 29, 143–155.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47(2), 263–292.
Landrieu, A., Mati, Y., & Binder, Z. (2001). A tabu search heuristic for the single vehicle pickup and delivery problem with time windows. Journal of Intelligent Manufacturing, 12, 497–508.
Laporte, G., Louveaux, F. V., & Mercure, H. (1989). Models and exact solutions for a class of stochastic location-routing problem. European Journal of Operational Research, 39, 71–78.
Liu, B. (2002). Theory and practice of uncertain programming. Heidelberg: Physica-Verlag.
Liu, B. (2007). Uncertainty theory (2nd ed.). Berlin: Springer.
Liu, B. (2008). Fuzzy process, hybrid process and uncertain process. Journal of Uncertain Systems, 2(1), 3–16.
Liu, B. (2009a). Some research problems in uncertainty theory. Journal of Uncertain Systems, 3(1), 3–10.
Liu, B. (2009b). Uncertain entailment and modus ponens in the framework of uncertain logic. Journal of Uncertain Systems, 3(4), 243–251.
Liu, B. (2009c). Theory and practice of uncertain programming (2nd ed.). berlin: Springer.
Liu, B. (2010a). Uncertain set theory and uncertain inference rule with application to uncertain control. Journal of Uncertain Systems, 4(2), 83–98.
Liu, B. (2010b). Uncertain risk analysis and uncertain reliability analysis. Journal of Uncertain Systems, 4(3), 163–170.
Liu, B. (2010c). Uncertainty theory: A branch of mathematics for modeling human uncertainty. Berlin: Springer.
Liu, B. (2011). Uncertain logic for modeling human language. Journal of Uncertain Systems, 5(1), 3–20.
Liu, B., & Yao, K. (2012). Uncertain multilevel programming: Algorithm and applications. Computers & Industrial Engineering. doi:10.1016/j.cie.2014.09.029.
Liu, Y. H., & Ha, M. H. (2010). Expected value of function of uncertain variables. Journal of Uncertain Systems, 4(3), 181–186.
Mu, R., Lan, Y., & Tang, W. (2013). An uncertain contract model for rural migrant worker’s employment problems. Fuzzy Optimization and Decision Making, 12(1), 29–39.
Qin, Z., & Kar, S. (2013). Single-period inventory problem under uncertain environment. Applied Mathematics and Computation, 219(18), 9630–9638.
Tillman, F. (1969). The multiple terminal delivery problem with probabilistic demands. Transportation Science, 3, 192–204.
Vahdani, B., Moghaddam, R. T., Zandieh, M., & Razmi, J. (2012). Vehicle routing scheduling using an enhanced hybrid optimization approach. Journal of Intelligent Manufacturing, 23(3), 759–774.
Yao, K. (2013). Extreme values and integral of solution of uncertain differential equation. Journal of Uncertainty Analysis and Applications, 1, Article 2.
Yao, K., & Chen, X. (2013). A numerical method for solving uncertain differential equations. Journal of Intelligent and Fuzzy Systems, 25(3), 825–832.
Yao, K., & Ji, X. Y. (2014). Uncertain decision making and its application to portfolio selection problem. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 22(1), 113–123.
Yao, K., & Li, X. (2012). Uncertain alternating renewal process and its application. IEEE Transcations on Fuzzy Systems, 20(6), 1154–1160.
Acknowledgments
This work was supported by the Humanities and Social Science Foundation of the Ministry of Education of China (10YJC63021) and National Natural Science Foundation of China (71402121).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Ning, Y., Su, T. A multilevel approach for modelling vehicle routing problem with uncertain travelling time. J Intell Manuf 28, 683–688 (2017). https://doi.org/10.1007/s10845-014-0979-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-014-0979-3