Abstract
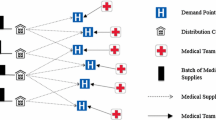
This paper employs uncertain programming to deal with a problem of dispatching medical supplies in emergency events. As we know, the highly unpredictable nature of emergencies and the severity of the accident may lead to uncertainty both in demands and running times. Under this condition, the demands and running times are supposed to be uncertain variables. Within the framework of uncertain programming, two mathematical models are constructed. In addition, some properties of the models are also discussed. Moreover, a hybrid intelligent algorithm for solving the proposed models in general cases is designed. Finally, some numerical examples are also presented to illustrate the optimization ideas and the effectiveness of the proposed algorithm.


Similar content being viewed by others
References
Barbarosoğlu, G., & Arda, Y. (2004). A two-stage stochastic programming framework for transportation planning in disaster response. Journal of the Operational Research Society, 55, 43–53.
Beraldi, P., Bruni, M. E., & Conforti, D. (2004). Designing robust emergency medical service via stochastic programming. European Journal of Operational Research, 158, 183–193.
Chang, M., Tseng, Y., & Chen, J. (2007). A scenario planning approach for the flood emergency logistics preparation problem under uncertainty. Transportation Research Part E: Logistics and Transportation Review, 43, 737–754.
Chen, X., & Ralescu, D. A. (2011). A note on truth value in uncertain logic. Expert Systems with Applications, 38, 15582–15586.
Daskin, M. S. (1987). Location, dispatching, and routing model for emergency services with stochastic travel times. In A. Ghosh & G. Rushton (Eds.), Spatial analysis and location-allocation models (pp. 76–84). New York: Van Nostrand Reinhold.
Dong, K., & Wang, N. (2013). Uncertain optimal control with application to vehicle routing problem. Information: An International Interdisciplinary Journal, 16, 1273–1278.
Fogel, D. (1994). An introduction to simulated evolutionary optimization. IEEE Transactions on Neural Networks, 5, 3–14.
Gao, Y., & Yao, K. (2014). Continuous dependence theorems on solutions of uncertain differential equations. Applied Mathematical Modelling, 38, 3031–3037.
Gen, M., & Cheng, R. (2000). Genetic algorithms and engineering optimization. New York: Wiley.
Holland, J. H. (1975). Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press.
Ingolfsson, A., Budge, S., & Erkut, E. (2008). Optimal ambulance location with random delays and travel times. Health Care Management Science, 11, 262–274.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263–292.
Li, X., & Liu, B. (2009a). Hybrid logic and uncertain logic. Journal of Uncertain Systems, 3, 83–94.
Li, X., & Liu, B. (2009b). Foundation of credibilistic logic. Fuzzy Optimization and Decision Making, 8, 91–102.
Li, X., & Wong, H. S. (2010). Credibilistic satisfiability and credibilistic entailment. Journal of Multiple-Valued Logic and Soft Computing, 16, 105–134.
Lin, L., Shinn, S., Gen, M., & Hwang, H. (2006). Network model and effective evolutionary approach for AGV dispatching in manufacturing system. Journal of Intelligent Manufacturing, 17, 465–477.
Liu, B. (2007). Uncertainty theory (2nd ed.). Berlin: Springer.
Liu, B. (2009a). Some research problems in uncertainty theory. Journal of Uncertain Systems, 3, 3–10.
Liu, B. (2009b). Theory and practice of uncertain programming (2nd ed.). Berlin: Springer.
Liu, B. (2010). Uncertainty theory: A branch of mathematics for modeling human uncertainty. Berlin: Springer.
Liu, B. (2012). Why is there a need for uncertainty theory? Journal of Uncertain Systems, 6, 3–10.
Liu, B. (2013a). Toward uncertain finace theory. Journal of Uncertainty Analysis and Applications, 1, Article 1.
Liu, B. (2013b). Extreme value theorems of uncertain process with application to insurance risk model. Soft Computing, 17, 549–556.
Mete, H. O., & Zabinsky, Z. B. (2010). Stochastic optimization of medical supply location and distribution in disaster management. International Journal of Production Economics, 126, 76–84.
Özdamar, L., Ekinici, E., & Kücükyazici, B. (2004). Emergency logistics planning in natural disasters. Annals of Operations Research, 129, 217–245.
Peng, J. (2013). Risk metrics of loss function for uncertain system. Fuzzy Optimization and Decision Making, 12, 53–64.
Peng, J., & Yao, K. (2011). A new option pricing model for stocks in uncertainty markets. International Journal of Operations Research, 8, 18–26.
Peng, Z., & Iwamura, K. (2010). A sufficient and necessary condition of uncertainty distribution. Journal of Interdisciplinary Mathematics, 13, 277–285.
Rathi, A. K., Church, R. L., & Solanki, R. S. (1992). Allocating resources to support a multicommodity flow with time windows. Transportation Research Part E: Logistics and Transportation Review, 28, 167–188.
Rodríguez, J. T., Vitoriano, B., & Montero, J. (2010). A natural-disaster management DSS for Humanitarian Non-Governmental Organisations. Knowledge-Based Systems, 23, 17–22.
Sheng, Y., & Yao, K. (2012). Fixed charge transportation problem in uncertain environment. Industrial Engineering and Management Systems, 11, 183–187.
Wang, C., & Chen, L. (2012). The heuristic preemptive dispatching method of material transportation system in 300 mm semiconductor fabrication. Journal of Intelligent Manufacturing, 23, 2047–2056.
Wang, X., & Peng, Z. (2014). Method of moments for estimating uncertainty distributions. Journal of Uncertainty Analysis and Applications, 2, Article 5.
Wen, M., & Iwamura, K. (2008). Facility location–allocation problem in random fuzzy environment: Using \((\alpha,\beta )\)-cost minimization model under the Hurewicz criterion. Computers and Mathematics with Applications, 55, 704–713.
Yang, X., & Gao, J. (2013). Uncertain differential games with application to capitalism. Journal of Uncertainty Analysis and Applications, 1, Article 17.
Yang, X., & Gao, J. (2014). Uncertain core for coalitional game with uncertain payoffs. Journal of Uncertain Systems, 8, 13–21.
Yang, L., Li, X., & Li, K. (2011). A fuzzy minimum risk model for the railway transportation planning problem. Iranian Journal of Fuzzy Systems, 8, 39–60.
Yao, K. (2013). Extreme values and integral of solution of uncertain differential equation. Journal of Uncertainty Analysis and Applications, 1, Article 2.
Yuan, Y., & Wang, D. (2009). Path selection model and algorithm for emergency logistics management. Computers and Industrial Engineering, 56, 1081–1094.
Zhang, B., & Peng, J. (2012). Uncertain programming model for Chinese postman problem with uncertain weights. Industrial Engineering and Management Systems, 11, 18–25.
Zhang, B., & Peng, J. (2013). Uncertain programming model for uncertain optimal assignment problem. Applied Mathematical Modelling, 37, 6458–6468.
Zhang, J., Li, J., & Liu, Z. (2012). Multiple-resource and multiple-depot emergency response problem considering secondary disasters. Expert Systems with Applications, 39, 11066–11071.
Zhu, Y. (2010). Uncertain optimal control with application to a portfolio selection model. Cybernetics and Systems, 41, 535–547.
Acknowledgments
This work is supported by the Projects of the Humanity and Social Science Foundation of Ministry of Education of China (No. 13YJA630065), the Key Project of Hubei Provincial Natural Science Foundation (No. 2012FFA065), and the Scientific and Technological Innovation Team Project (No. T201110) of Hubei Provincial Department of Education, the Fundamental Research Funds for the Central Universities (No. 31541411209), China.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Li, H., Peng, J., Li, S. et al. Dispatching medical supplies in emergency events via uncertain programming. J Intell Manuf 28, 549–558 (2017). https://doi.org/10.1007/s10845-014-1008-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10845-014-1008-2