Intelligent information sharing among manufacturers in supply networks: supplier selection case

Abstract

Decision making in highly distributed supply networks has become more complex in globally dynamic markets. Despite extensive previous work on supply network decisions, it is still necessary to develop advanced tools for selective collection, management, and sharing of relevant information. In this research, a new intelligent, distributed, and autonomous information sharing protocol is modelled and applied to analytically determine supplier information sharing among manufacturers. Information sharing with all manufacturers is neither sensible nor realistic, since it requires high communication/implementation costs and cannot guarantee a positive return to all parties. Our Intelligent Supplier Information Sharing (ISIS) protocol supports each manufacturer’s decision-making process on selective information sharing. It does so by analyzing the expected sharing benefit while estimating the value of other parties’ information. Through a negotiation process, the appropriate price for shared information that each manufacturer has to pay is also determined. Numerical examples illustrate the performance of the ISIS protocol. Compared to no sharing and complete sharing of information, selective sharing recommended by ISIS yields relatively higher profits. For the case analyzed, profit increase by ISIS is, on average, 15.5 % higher than with complete information sharing, and this advantage holds even under changing conditions.

Appendix

Proof of Theorem 1:

Consider company A’s position; all of company A’s information is known and partial information about company B’s suppliers is provided $\left( \overline{{{x_k ^{B}}}}\right)$. For convenience, all $w_k ^{A}$ and $w_k ^{B}$ are set as one because they do not affect the relationship between VI and expected profit-increase.

• Case 1: $m=1, n\ge 1$

In this case, partial information is the same as complete information. Hence, ISIS protocol is not necessary.

• Case 2: $m=2,\,n=1$

  For convenience, simplified notations, $x_1$ and $x_2$ are used instead of $x_{1,1} ^{A}$ and $x_{2,1} ^{A}$; also, $y_1$ and $y_{2}$are used instead of $x_{1,1} ^{B}$ and $x_{2,1} ^{B}$; and $\mu$ and $\sigma$ are regarded as $\mu _k$ and $\sigma _k$, respectively. $x_1$ and $x_2$ are identified as follows: $x_1 =min\left( {x_1 ,x_2 } \right)$ and $x_2 =max\left( {x_1 ,x_2 } \right)$. In this case, $VI^{B}$ is represented as in Eq. (12) by using Eq. (10).

$$\begin{aligned} VI^{B}=\bar{y}-\bar{x} =\left( {y_1 +y_2 } \right) /2-\left( {x_1 +x_2 } \right) /2 \end{aligned}$$

(12)

Because $x_1$, $x_2$, $y_1$, and $y_2$ are assumed to follow a Normal distribution (according to the assumptions in the notation), company A’s expected profit-increase can be estimated in two cases, as shown below.

• i. $x_2 \le \bar{y}$

  $$\begin{aligned} E\left( {p^{A}} \right)= & {} \int _{-\infty }^{\bar{{y}}} {\frac{r}{\sqrt{2\pi }\sigma }} \cdot \left( {2\bar{{y}}-y_1 -x_2 } \right) \nonumber \\&\times \cdot exp\left( {-\frac{\left( {\bar{{y}}-y_1 } \right) ^{2}}{\sigma ^{2}}} \right) dy_1 \nonumber \\&+ \int _{\bar{{y}}}^\infty \frac{r}{\sqrt{2\pi }\sigma }\cdot \left( {y_1 -x_2 } \right) \nonumber \\&\times \cdot exp\left( {-\frac{\left( {\bar{{y}}-y_1 } \right) ^{2}}{\sigma ^{2}}} \right) dy_{1}\nonumber \\= & {} \frac{r}{\sqrt{2\pi }}\cdot \left\{ {\sigma +\sqrt{\pi \cdot }\left( {{\bar{y}}-x_2 } \right) } \right\} \end{aligned}$$

  (13)

• ii. $x_2 >\bar{y}$

  $$\begin{aligned} E\left( {p^{A}} \right)= & {} \int _{-\infty }^{2{\bar{y}}-x_2} \frac{r}{\sqrt{2\pi }\sigma }\cdot (2\bar{{y}}-y_1 -x_2 )\nonumber \\&\times \cdot exp\left( {-\frac{\left( {\bar{{y}}-y_1 } \right) ^{2}}{\sigma ^{2}}} \right) dy_1 +\int _{2{\bar{y}}-x_2 }^{x_2 } 0\cdot dy_1\nonumber \\&+\int _{x_2 }^{\infty }\frac{r}{\sqrt{2\pi }\sigma }\cdot \left( {y_1 -x_2 } \right) \nonumber \\&\times \cdot exp\left( {-\frac{\left( {\bar{{y}}-y_1 } \right) ^{2}}{\sigma ^{2}}} \right) dy_1\nonumber \\= & {} \frac{r}{\sqrt{2\pi }}\cdot \left\{ \sqrt{\pi }\cdot \left( {\bar{{y}}-x_2 } \right) \cdot \left( {erf\left( {\frac{\bar{{y}}-x_2 }{\sigma }} \right) +1} \right) \right. \nonumber \\&+\left. \sigma \cdot exp\left( {-\frac{\left( {\bar{{y}}-x_2 } \right) ^{2}}{\sigma ^{2}}} \right) \right\} \end{aligned}$$

  (14)

  $\therefore$ In both cases,

  $$\begin{aligned} \partial \left( {E\left( {p^{A}} \right) } \right) /\partial \left( {\bar{y}-x_2 } \right) >0 \end{aligned}$$

  (15)

  $E\left( {p^{A}} \right)$ increases as the value of $\bar{y}-x_2$ is larger. It means that $E\left( {p^{A}} \right)$ increases as $VI^{B}$ increases.

• Case 3: $m\ge 2,\,n=2$

The number of sustainability factors does not affect the relationship between VI and expected profit-increase because $w_k ^{A}$ and $w_k ^{B}$ are consistently considered in calculating both $VI^{B} \quad \left( {VI^{A}} \right)$ and $\left( {p^{A}} \right) \quad \left( {E\left( {p^{B}} \right) } \right)$. Hence, the result is the same as in Case 2.

• Case 4: $m\ge 3,\,n=1$

As in Case 2, we use simplified notation as $x_1 ,\,x_2 ,\ldots ,\,x_m \,\hbox {and}\,y_1 ,\,y_{2 } ,\ldots ,y_m$ instead of $x_{1,1}^{A}$, $x_{2,1} ^{A},\ldots ,x_{m,1} ^{A}$ and $x_{1,1} ^{B}$, $x_{2,1} ^{B},\ldots ,x_{m,1} ^{B}$; and $\mu$ and $\sigma$ are regarded as $\mu _k$ and $\sigma _k$, respectively. To find out the posterior distribution of $y_1 ,\ldots ,\,y_m$, the case when n is 2 is considered.

Set u as in Eq. (16).

$$\begin{aligned} y_1 +y_2 =x_1 +x_2 +2\cdot VI^{B}=u \end{aligned}$$

(16)

Then, $E\left( {p^{A}} \right)$ can be calculated as shown below.

$$\begin{aligned} E\left( {p^{A}} \right)= & {} r\cdot \left\{ {max \left( {y_1 ,\,y_2 } \right) -x_2 } \right\} ^{+}\cdot Pr(Y_1 =y_1 , Y_2 =y_2 ) \nonumber \\= & {} r\cdot \left\{ {max \left( {y_1 ,\,y_2 } \right) -x_2 } \right\} ^{+}\nonumber \\&\times \cdot Pr(Y_1 =y_1 ,\,Y_2 =u-y_1 ) \end{aligned}$$

(17)

The posterior distribution of $y_1$ and $y_2$ is represented as shown in Eq. (18e) by the following procedure.

$$\begin{aligned}&Pr \left( {Y_1 =y_1,\,Y_2 =y_2 |y_1 +y_2 =u} \right) \qquad u\sim N(2\mu , \sqrt{2}\sigma )\end{aligned}$$

(18a)

$$\begin{aligned}&\quad =Pr \left( {Y_1 =y_1 ,\,Y_2 =u-y_1 |y_1 +y_2 =u} \right) \end{aligned}$$

(18b)

$$\begin{aligned}&\quad =Pr \left( {Y_1 =y_1 ,\,Y_2 =u-y_1 } \right) /Pr \left( {y_1 +y_2 =u} \right) \end{aligned}$$

(18c)

$$\begin{aligned}&\quad \propto Pr \left( {Y_1 =y_1 ,\,Y_2 =u-y_1 } \right) \end{aligned}$$

(18d)

$$\begin{aligned}&\quad \propto exp\left( {-\frac{1}{2\sigma ^{2}}\left\{ {(y_1 -\mu )^{2}+\left( {\left( {u-y_1 } \right) -\mu } \right) ^{2}} \right\} } \right) \end{aligned}$$

(18e)

The result can be further represented as in Eqs. (19) and (20) by summarizing with $\hbox {y}_1.$

$$\begin{aligned}&\Pr \left( {Y_1 =y_1 ,\,Y_2 =y_2 |y_1 +y_2 =u} \right) \propto exp\left( {-2(y_1 -u/2)^{2}} \right) \end{aligned}$$

(19)

$$\begin{aligned}&\therefore \left( {{\begin{array}{l} {y_1 } \\ {y_2 } \\ \end{array} }} \right) \sim \mathbf{N}\left( {\left( {{\begin{array}{l} {\frac{u}{2}} \\ {\frac{u}{2}} \\ \end{array} }} \right) ,\left( {{\begin{array}{ll} {\left( {\frac{\sigma }{\sqrt{2}}} \right) ^{2}}&{} {\left( {\frac{\sigma }{\sqrt{2}}} \right) ^{2}} \\ {\left( {\frac{\sigma }{\sqrt{2}}} \right) ^{2}}&{} {\left( {\frac{\sigma }{\sqrt{2}}} \right) ^{2}} \\ \end{array} }} \right) } \right) \end{aligned}$$

(20)

Through the same procedure, the posterior distribution of $y_1,\,y_2 ,\ldots ,y_n$ in case n is larger than 2 is as in Eq. (23).

$$\begin{aligned}&{\bar{x}}=\left( {x_1 +x_2 +\ldots +x_n } \right) /n,{\bar{y}}=\left( {y_1 +y_2 +\ldots +y_n } \right) /n \end{aligned}$$

(21)

$$\begin{aligned}&u=n*\bar{y} =n*\left( {\bar{x} +VI^{B}} \right) \end{aligned}$$

(22)

$$\begin{aligned}&\left( {{\begin{array}{l} {y_1 } \\ \vdots \\ {y_n } \\ \end{array} }} \right) \sim \mathbf{N}\left( {\left( {{\begin{array}{l} {u/n} \\ \vdots \\ {u/n} \\ \end{array} }} \right) ,\left( {{\begin{array}{lll} {\left( {\sigma /{\sqrt{n}}} \right) ^\mathbf{2}}&{} \ldots &{} \vdots \\ \vdots &{} \ldots &{} \vdots \\ \vdots &{} \ldots &{} {\left( {\sigma /{\sqrt{n}}} \right) ^\mathbf{2}} \\ \end{array} }} \right) } \right) \nonumber \\ \end{aligned}$$

(23)

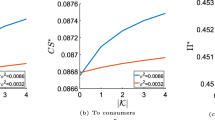
As $VI^{B}$ increases, the probability that $y_1 ,\ldots ,y_n$ will be larger also increases. It means that company A has more chance to yield a profit by finding better supplier based on company B’s information as $VI^{B}$ increases, i.e., $E\left( {p^{A}} \right)$ increases as $VI^{B}$ is larger.

• Case 5: $m\ge 3,\,n\ge 2$

The result is the same as in Case 4 by the same reason explained in Case 3.

Also, based on the proof of Theorem 1, there is a consistent relationship between variance of suppliers’ sustainability scores $(\sigma _k ^{2})$ and expected profit-increase by the information sharing as shown below.

Proof of Theorem 2:

Theorem 2 is intuitively proven. As $\sigma _k$ is larger, the possibility to find better supplier fitting to each manufacturer’s preference from the other company’s suppliers increases; especially, when the number of suppliers each manufacturer knows is smaller, the expected benefit from the sharing is significantly increased as $\sigma _k$ is larger. Further mathematical proof is as follows.

Assume that all sustainability factors follow a same Normal distribution to simplify, i.e., $\upmu$ and $\upsigma$ are regarded as $\mu _k$ and $\sigma _k$, respectively. And, consider five cases, same as in the proof of Theorem 1.

• Case 1: $m=1,\,n\ge 1$

In this case, partial information is the same as complete information. Therefore, there is no meaning to a larger $\upsigma$.

• Case 2: $m=2,\,n=1$

With the same settings in Case 2 in the proof of Theorem 1, Eqs. (13) and (14) are obtained, and used to consider the effect of larger $\upsigma$ as below. Eq. (24) is the derivative of Eq. (13) with respect to $\sigma$; and Eq. (25) is the derivative of Eq. (14) with respect to $\sigma$.

• i. $x_2 \le \bar{y}$

  $$\begin{aligned} \frac{\partial \left( {E\left( {p^{A}} \right) } \right) }{\partial \sigma }=\frac{r}{\sqrt{2\pi }}>0 \end{aligned}$$

  (24)

• ii. $x_2 >\bar{y}$

  $$\begin{aligned} \frac{\partial \left( {E\left( {p^{A}} \right) } \right) }{\partial \sigma }=\frac{r}{\sqrt{2\pi }}\cdot exp\left( {-\frac{\left( {\bar{y}-x_2 } \right) ^{2}}{\sigma ^{2}}} \right) >0 \end{aligned}$$

  (25)

  Therefore, as $\sigma$ increases, the profit-increase of company A is also increased. This result is also the same for company B.

• Case 3: $m\ge 2,\,n=2$

The number of sustainability factors does not affect the relationship between $\sigma$ and expected profit-increase for the same reason explained in Case 3 in the proof of Theorem 1.

• Case 4: $m\ge 3,\,n=1$

With the same settings in Case 4 in the proof of Theorem 1, Eq. (23) is obtained, and used to consider the effect of larger $\sigma$. As $\sigma$ increases, the probability that $y_1 ,\ldots ,y_n$ will be large also increases. It means that company A has more chance to yield a profit by finding better supplier from company B’s information as $\upsigma$ increases. In the case of company B, this result is also the same.

• Case 5: $m\ge 3,\,n\ge 2$

The result is the same as in Case 4 by the same reason explained in Case 3.