Skip to main content

Advertisement

Springer Nature Link
Log in

Optimal control model for finite capacity continuous MRP with deteriorating items

  • Published:
Journal of Intelligent Manufacturing Aims and scope Submit manuscript

Abstract

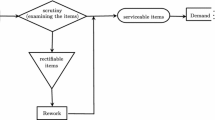
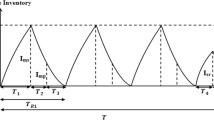
A general model for continuous material requirements planning problem is proposed which contains of reworking of returned items along with deterioration of items. In the proposed model there are separated stocks for manufactured, returned and reworked items and also it is possible to consider returned items from both inventories of manufactured and reworked items. A general finite time linear quadratic optimal control problem is presented to attain the goal values for inventories, demands and productions. The goal values for inventories, demands and production can be considered as the capacity of stocks, scheduled demand and capacity of transportation respectively. Since the time is considered as a continuous parameter, the carrying cost of production process is more real than the periodic approach wherein time is considered as a discrete parameter. Finally a solution method is presented and numerical simulations are provided to validate the approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Benkherouf, L., Skouri, K., & Konstantaras, I. (2016). Optimal control of production, remanufacturing and refurbishing activities in a finite planning horizon inventory system. Journal of Optimization Theory and Applications, 168, 677–698.

    Article  Google Scholar 

  • Daz-Madroero, M., Mula, J., Jimnez, M., & Peidro, D. (2017). A rolling horizon approach for material requirement planning under fuzzy lead times. International Journal of Production Research, 55(8), 2197–2211.

    Article  Google Scholar 

  • Dong, Mi, Heb, F., & Wu, Z. (2011). Optimal control of a continuum model for single-product re-entrant manufacturing systems. International Journal of Production Research, 49, 6363–6385.

    Article  Google Scholar 

  • Effati, S., & Pakdaman, M. (2013). Optimal control problem via neural networks. Neural Computing and Applications, 23(7–8), 2093–2100.

    Article  Google Scholar 

  • Foul, A., Djemili, S., & Tadj, L. (2007). Optimal and self-tuning optimal control of a periodic-review hybrid production inventory system. Nonlinear Analysis: Hybrid Systems, 1(1), 68–80.

    Google Scholar 

  • Foul, A., & Tadj, L. (2006). Optimal control of a hybrid periodic-review production inventory system with disposal. International Journal of Operational Research, 2(4), 481–494.

    Article  Google Scholar 

  • Foul, A., Tadj, L., & Hedjar, R. (2012). Adaptive control of inventory systems with unknown deterioration rate. Journal of King Saud University Science, 24, 215–220.

    Article  Google Scholar 

  • Geetha, K. V., & Uthayakumar, R. (2009). Optimal inventory control policy for items with time-dependent demand. American Journal of Mathematical and Management Sciences, 29, 457–476.

    Article  Google Scholar 

  • Grubbstrom, R. W., Bogataj, M., & Bogataj, L. (2010). Optimal lotsizing within MRP theory. Annual Reviews in Control, 34, 89–100.

    Article  Google Scholar 

  • Grubbstrom, R. W., & Tang, O. (2012). The space of solution alternatives in the optimal lotsizing problem for general assembly systems applying MRP theory. International Journal of Production Economics, 140, 765–777.

    Article  Google Scholar 

  • Guchhait, P., Maiti, M. K., & Maiti, M. (2014). Inventory policy of a deteriorating item with variable demand under trade credit period. Computers & Industrial Engineering, 76, 75–88.

    Article  Google Scholar 

  • Hedjara, R., Bounkhel, M., & Tadj, L. (2005). Receding horizon control of a hybrid production system with deteriorating items. Nonlinear Analysis, 63, 405–422.

    Article  Google Scholar 

  • Hedjar, R., Garg, A. K., & Tadj, L. (2015). Model predictive production planning in a three-stock reverse-logistics system with deteriorating items. International Journal of Systems Science: Operations & Logistics, 2, 187–198.

    Google Scholar 

  • Hedjar, R., Tadj, L., & Abid, C. (2012). Optimal control of integrated production-forecasting system. In: Jao, C. (ed.), Decision support systems. In-tech series in numerical analysis and scientific computing, 2012. ISBN: 978-953-51-0799-6.

  • Hosseini, S., & Al Khaled, A. (2014). A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research. Applied Soft Computing, 24, 1078–1094.

    Article  Google Scholar 

  • Hosseini, S., & Barker, K. (2016). A Bayesian network model for resilience-based supplier selection. International Journal of Production Economics, 180, 68–87.

    Article  Google Scholar 

  • Ignaciuk, P., & Bartoszewicz, A. (2010). Linearquadratic optimal control strategy for periodic-review inventory systems. Automatica, 46, 1982–1993.

    Article  Google Scholar 

  • Jodlbauer, H., & Reitner, S. (2012). Material and capacity requirements planning with dynamic lead times. International Journal of Production Research, 50(16), 4477–4492.

    Article  Google Scholar 

  • Louly, M.-A., Dolgui, A., & Al-Ahmari, A. (2012). Optimal MRP offsetting for assembly systems with stochastic lead times: POQ policy and service level constraint. Journal of Intelligent Manufacturing, 23, 2485–2495.

    Article  Google Scholar 

  • Mezghiche, A., Moulai, M., & Tadj, L. (2015). Model predictive control of a forecasting production system with deteriorating items. International Journal of Operations Research and Information Systems, 6(4), 19–37.

    Article  Google Scholar 

  • Milne, R. J., Mahapatra, S., & Wang, C.-T. (2015). Optimizing planned lead times for enhancing performance of MRP systems. International Journal of Production Economics, 167, 220–231.

    Article  Google Scholar 

  • Minner, S., & Kleber, R. (2001). Optimal control of production and remanufacturing in a simple recovery model with linear cost functions. OR Spektrum, 23, 3–24.

    Article  Google Scholar 

  • Mishra, U. (2016). An EOQ model with time dependent Weibull deterioration, quadratic demand and partial backlogging. International Journal of Applied and Computational Mathematics. https://doi.org/10.1007/s40819-015-0077-z.

  • Mula, J., Lyons, A. C., Hernndez, J. E., & Poler, R. (2014). An integer linear programming model to support customer-driven material planning in synchronised, multi-tier supply chains. International Journal of Production Research, 52(14), 4267–4278.

    Article  Google Scholar 

  • Mula, J., Poler, R., & Garcia-Sabater, J. P. (2007). Material requirement planning with fuzzy constraints and fuzzy coefficients. Fuzzy Sets and Systems, 158(7), 783–793.

    Article  Google Scholar 

  • Pakdaman, M., & Effati, S. (2016). Approximating the solution of optimal control problems by fuzzy systems. Neural Processing Letters, 43(3), 667–686.

    Article  Google Scholar 

  • Paopongchuang, B., & Yenradee, P. (2014). Finite capacity material requirement planning with supplier constraints. International Journal of Industrial and Systems Engineering, 17(3), 350–375.

    Article  Google Scholar 

  • Pooya, A., & Faezirad, M. (2017). A taxonomy of manufacturing strategies and production systems using self-organizing map. Journal of Industrial and Production Engineering, 34, 300–311.

    Article  Google Scholar 

  • Pooya, A., & Pakdaman, M. (2017a). Analysing the solution of production-inventory optimal control systems by neural networks. RAIRO-Operations Research, 51, 577–590.

    Article  Google Scholar 

  • Pooya, A., & Pakdaman, M. (2017a). A delayed optimal control model for multi-stage production-inventory system with production lead times. The International Journal of Advanced Manufacturing Technology. https://doi.org/10.1007/s00170-017-0942-5.

  • Pooya, A., Pakdaman, M., & Tadj, L. (2017). Exact and approximate solution for optimal inventory control of two-stock with reworking and forecasting of demand. Operational Research. https://doi.org/10.1007/s12351-017-0297-6.

  • Ram, B., Naghshineh-Pour, M. R., & Yu, X. (2006). Material requirements planning with flexible bills-of-material. International Journal of Production Research, 44(2), 399–415.

    Article  Google Scholar 

  • Riezebos, J., & Zhu, X. (2015). MRP planned orders in a multiple-supplier environment with differing lead times. Production and Operations Management, 24, 883–895.

    Article  Google Scholar 

  • Rossi, T., Pozzi, R., Pero, M., & Cigolini, R. (2017). Improving production planning through finite capacity MRP. International Journal of Production Research. https://doi.org/10.1080/00207543.2016.1177235.

  • Sadeghian, R. (2011). Continuous materials requirements planning (CMRP) approach when order type is lot for lot and safety stock is zero and its applications. Applied Soft Computing, 11, 5621–5629.

    Article  Google Scholar 

  • Segerstedt, A. (2017). Cover-time planning/takt planning: A technique for materials requirement and production planning. International Journal of Production Economics, 194, 25–31.

    Article  Google Scholar 

  • Subbaram Naidu, D. (2002). Optimal control systems. Boca Raton: CRC Press.

    Google Scholar 

  • Sukkerd, W., & Wuttipornpun, T. (2016). Hybrid genetic algorithm and tabu search for finite capacity material requirement planning system in flexible flow shop with assembly operations. Computers and Industrial Engineering, 97, 157–169.

    Article  Google Scholar 

  • Sun, Y., & Zhu, Y. (2017). Bangbang property for an uncertain saddle point problem. Journal of Intelligent Manufacturing. https://doi.org/10.1007/s10845-014-1003-7.

  • Swamidass, P. M. (2000). Encyclopedia of production and manufacturing management. Berlin: Springer.

    Book  Google Scholar 

  • Vercraene, S., & Gayon, J.-P. (2013). Optimal control of a production-inventory system with product returns. International Journal of Production Economics, 142, 302–310.

    Article  Google Scholar 

  • Wuttipornpun, T., & Yenradee, P. (2004). Development of finite capacity material requirement planning system for assembly operations. Production Planning & Control, 15(5), 534–549.

    Article  Google Scholar 

  • Wuttipornpun, T., & Yenradee, P. (2007). Performance of TOC based finite capacity material requirement planning system for a multi-stage assembly factory. Production Planning and Control, 18(8), 703–715.

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the editor and anonymous referees for their constructive comments. This work was supported in part by: Research Deputy of Ferdowsi University of Mashhad, under Grant No. 39098 (dated Feb. 28, 2016).

Author information

Authors and Affiliations

  1. Department of Management, Ferdowsi University of Mashhad, Mashhad, Iran

    Alireza Pooya

  2. Climatological Research Institute, Mashhad, Iran

    Morteza Pakdaman

Authors
  1. Alireza Pooya
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Morteza Pakdaman
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Alireza Pooya.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pooya, A., Pakdaman, M. Optimal control model for finite capacity continuous MRP with deteriorating items. J Intell Manuf 30, 2203–2215 (2019). https://doi.org/10.1007/s10845-017-1383-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10845-017-1383-6

Keywords