Abstract
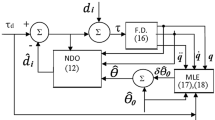
In this paper a tracking controller expressed in terms of the normalized quasi-velocities (NQV) for rigid manipulators is proposed. These quasi-velocities introduced by [Jain and Rodriguez, IEEE Trans. Robot. Autom., 11:571–584, 1995] are utilized here in order to reveal some useful features which are observable if we track a desired quasi-velocity trajectory. The presented controller in terms of NQV is exponentially convergent. Moreover, some geometrical interpretation of the normalized quasi-variables based on Riemannian geometry is given. It is shown that the controller can be helpful for evaluation and reduction of dynamical couplings existing in the system. As a result it is helpful at the design step of manipulators. The control strategy was tested in simulation on two 3 d.o.f. spatial manipulators.
Similar content being viewed by others
Abbreviations
- \({\cal N}\) :
-
number of degrees of freedom
- \({{\theta}},\dot{{\theta}},\ddot{{\theta}} \in R^{\cal N}\) :
-
vectors of generalized positions, velocities, and accelerations, respectively
- \({{M}}({\theta}) \in R^{{\cal N}\times {\cal N}}\) :
-
system mass matrix
- \(C({\theta},\dot{{\theta}})=\dot{{M}}\dot{{\theta}}-\frac{1}{2}\dot{{\theta}}^T {M}_{{\theta}}\dot{{\theta}} \in R^{\cal N}\) :
-
vector of Coriolis and centrifugal forces in classical equations of motion, where the expression \(\dot{{\theta}}^T {M}_{{\theta}}\dot{{\theta}}\) is the column vector \({col}(\dot{{\theta}}^T {M}_{{\theta}_k}\dot{{\theta}}), {M}_{{\theta}_k}=\frac{\partial {M}}{\partial {\theta}_k}\) denotes the partial derivative of the mass matrix \({{M}}({\theta})\) and \(\dot{{M}}\) is its time derivative [9]
- \(G({\theta}) \in R^{\cal N}\) :
-
vector of gravitational forces in classical equations of motion
- \({\tau} \in R^{\cal N}\) :
-
vector of generalized forces
- \({\nu} \in R^{\cal N}\) :
-
vector of normalized quasi-velocities (NQV)
- \({H} \in R^{{\cal N}\times 6{\cal N}}\) :
-
projection operator for all joint axes
- \({{P}} \in R^{6{\cal N}\times 6{\cal N}}\) :
-
articulated inertia matrix
- \({D}={H}{P}{H}^{T} \in R^{{\cal N}\times {\cal N}}\) :
-
articulated inertia about joint axes, a diagonal matrix \({{D}}={D}({\theta})\)
- \(C_{\nu}({{\theta}},{{\nu}})=m^{-1}(\theta)C(\theta,\dot{\theta})-\dot{m}^{T}(\theta)\dot{\theta} \in R^{\cal N}\) :
-
vector of Coriolis and centrifugal forces in equations of motion expressed in terms of NQV vector
- \(G_{\nu}({\theta})=m^{-1}(\theta)G(\theta) \in {R}^{\cal N}\) :
-
vector of gravitational forces in equations of motion expressed in terms of NQV vector
- \({m}({{\theta}}) \in R^{{\cal N}\times {\cal N}}\) :
-
spatial operator "square root" of mass \(M({\theta})\), namely \(M({\theta})=m({\theta}){{{m}}}^{{T}}({\theta})\)
- \(\dot{{m}}({{\theta}}) \in R^{{\cal N}\times {\cal N}}\) :
-
time derivative of factor \({m}({{\theta}})\)
- \({\epsilon}=m^{-1}(\theta)\tau \in {R}^{\cal N}\) :
-
vector of normalized quasi-moments,
- \((.)^{T}\) :
-
transpose operation
References
Arnold, V.I.: Mathematical Methods of Classical Mechanics. Springer, Berlin Heidelberg New York (1989)
Bronsztein, I.N., Siemiendiaiev, K.A.: Mathematical Handbook. Nauka, Moscow (in Russian) (1980)
Canudas de Wit, C., Siciliano, B., Bastin, G. (eds.): Theory of Robot Control. Springer, Berlin Heidelberg New York (1996)
Cotsaftis, M., Robert, J., Rouff, M., Vibet, C.: Applications and prospect of the nonlinear decoupling method. Comput. Methods Appl. Mech. Engrg. 154, 163–178 (1998)
Gu, Y.L.: Configuration manifolds and their applications to robot dynamic modeling and control. IEEE Trans. Robot. Autom. 16, 517–527 (2000)
Gu, Y.-L., Loh, N.K.: Control system modelling for robot manipulators by use of a canonical transformation. In: Proc. IEEE Conf. on Robotics and Automation, Raleyigh, North Carolina, pp. 484–489 (1987)
Herman, P., Kozłowski, K.: A comparison of certain quasi-velocities approaches in PD joint space control. In: Proc. of the IEEE Int. Conf. on Robotics and Automation, pp. 3819–3824. Seoul, Korea, 21–26 May 2001
Jain, A., Rodriguez, G.: Diagonalized Lagrangian robot dynamics. IEEE Trans. Robot. Autom. 11, 571–584 (1995)
Koditschek, D.: Robot kinematics and coordinate transformations. In: Proc. of the 24th IEEE Conf. on Decision and Control, pp. 1–4. Fort Lauderdale, Florida (1985)
Kozłowski, K.: Mathematical dynamic robot models and identification of their parameters. Technical University of Poznań Press, Poznań (in Polish) (1992)
Kozłowski, K., Herman, P.: A comparison between PD-Controls in terms of normalized and unnormalized quasi-velocities. In: Morecki, A., Bianchi, G., Rzymkowski, C. (eds.) Proc. of the Thirteenth CISM-IFToMM Symposium ROMANSY 13 Theory and Practice of Robots and Manipulators, pp. 215–222. Springer, Berlin Heidelberg New York (2000)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. Springer, Berlin Heidelberg New York (1994)
Reyes, F., Kelly, R.: Experimental evaluation of model-based controllers on a direct-drive robot arm. Mechatronics 11, 267–282 (2001)
Rodriguez, G., Jain, A., Kreutz-Delgado, K.: A spatial operator algebra for manipulator modeling and control. Int. J. Rob. Res. 10, 371–381 (1991)
Sciavicco, L., Siciliano, B.: Modeling and Control of Robot Manipulators. McGraw-Hill, New York (1996)
Spong, M.: Remarks on robot dynamics: canonical transformations and Riemannian geometry. In: Proc. IEEE Conf. on Robotics and Automation, pp. 554–559. Nice, France (1992)
Spong, M.: On feedback linearization of robot manipulators and Riemannian curvature, robotics workshop, pp. 1–20. Minneapolis, Minnesota (January, 1993)
Wen, J.T., Bayard, D.S.: New class of control laws for robotic manipulators. Part 1. Non-adaptive case. Int. J. Cont. 47, 1361–1385 (1998)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Herman, P. Tracking Controller Using Normalized Quasi-velocities. J Intell Robot Syst 47, 87–100 (2006). https://doi.org/10.1007/s10846-006-9073-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10846-006-9073-1