Abstract
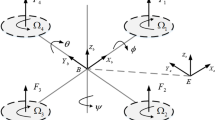
The dynamics of a quadrotor are a simplified form of helicopter dynamics that exhibit the same basic problems of underactuation, strong coupling, multi-input/multi-output design, and unknown nonlinearities. Control design for the quadrotor is more tractable yet reveals corresponding approaches for helicopter and UAV control design. In this paper, a backstepping approach is used for quadrotor controller design. In contrast to most other approaches, we apply backstepping on the Lagrangian form of the dynamics, not the state space form. This is complicated by the fact that the Lagrangian form for the position dynamics is bilinear in the controls. We confront this problem by using an inverse kinematics solution akin to that used in robotics. In addition, two neural nets are introduced to estimate the aerodynamic components, one for aerodynamic forces and one for aerodynamic moments. The result is a controller of intuitively appealing structure having an outer kinematics loop for position control and an inner dynamics loop for attitude control. The control approach described in this paper is robust since it explicitly deals with unmodeled state-dependent disturbances and forces without needing any prior knowledge of the same. A simulation study validates the results obtained in the paper.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Koo, T.J., Sastry, S.: Output tracking control design of a helicopter model based on approximate linearization. In: Proceedings of the 37th Conference on Decision and Control. Tampa, Florida (1998)
Stevens, B.L., Lewis, F.L.: Aircraft Control and Simulation. Wiley, New York (2003)
Castillo, P., Lozano, R., Dzul, A.: Modelling and Control of Mini Flying Machines. Springer, Berlin (2005)
Bouabdallah, S., Noth, A., Siegwart, R.: PID vs LQ control techniques applied to an weight augmentation high energy consumption indoor micro quadrotor. In: Proceedings of 2004 1EEElRS.J Internationel Conference on Intelligent Robots and Systems. Sendal, Japan (2004)
Madani, T., Benallegue, A.: Backstepping control for a quadrotor helicopter. In: Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, China (2006)
Mokhtari, A., Benallegue, A., Orlov, Y.: Exact linearization and sliding mode observer for a quadrotor unmanned aerial vehicle. Int. J. Robot. Autom. 21, 39–49 (2006). doi:10.2316/Journal.206.2006.1.206-2842
Mokhtari, A., Benallegue, A., Daachi, B.: Robust feedback linearization and GH∞ controller for a quadrotor unmanned aerial vehicle. J. Electr. Eng. 57, 20–27 (2006)
Kim, H.J., Shim, D.H., Sastry, S.: Nonlinear model predictive tracking control for rotorcraft-based unmanned aerial vehicles. In: Proceedings of the American Control Conference. Anchorage, AK (2002)
Kanellakopoulos, I., Kokotovic, P.V., Morse, A.S.: Systematic design of adaptive controllers for feedback linearizable systems. IEEE Trans. Automat. Contr. 36, 1241–1253 (1991). doi:10.1109/9.100933
Castillo, P., Dzul, A., Lozano, R.: Real-time stabilization and tracking of a four-rotor mini rotorcraft. IEEE Trans. Contr. Syst. Technol. 12, 510–516 (2004). doi:10.1109/TCST.2004.825052
Castillo, P., Lozano, R., Dzul, A.: Stabilization of a mini rotorcraft having four rotors. IEEE Contr. Syst. Mag. 25, 45–55 (2005). doi:10.1109/MCS.2005.1550152
Bouabdallah, S., Noth, A., Siegwart, R.: PID vs LQ control techniques applied to an indoor micro quadrotor. In: International Conference on Intelligent Robots and Systems, pp. 2451–2456 (2004)
Mahony, R., Hamel, T.: Robust trajectory tracking for a scale model autonomous helicopter. Int. J. Robust Nonlinear Contr. 14, 1035–1059 (2005). doi:10.1002/rnc.931
Yang, C.D., Liu, W.H.: Nonlinear Hoo Decoupling hover control of helicopter with parameter uncertainties. In: Proceedings of the American Control Conference. Denver, Colorado (2003)
Enns, R., Si, J.: Helicopter flight control design using a learning control Approach1. In: Proceedings of the 39th Conference on Decision and Control. Sydney, Australia (2000)
Calise, A.J., Kim, B.S., Leitner, J., Prasad, J.V.R.: Helicopter adaptive flight control using neural networks. In: Proceedings of the 33rd Conference on Decision and Control. Lake Buena Vista, FL (1994)
Johnson, E., Kannan, S.: Adaptive trajectory control for autonomous helicopters. AIAA J. Guid. Control Dyn. 28, 524–538 (2005). doi:10.2514/1.6271
Farrell, J., Sharma, M., Polycarpou, M.: Backstepping-based flight control with adaptive function approximation. AIAA J. Guid. Contr. Dyn. 28, 1089–1102 (2005)
Hamel, T., Mahony, R., Lozano, R., Ostrowski, J.: Dynamic modeling and configuration stabilization for an X4-flyer. In: IFAC 15th Triennial World Congress. Barcelona, Spain (2002)
Mistler, V., Benallegue, A., M’Sirdi, N.K.: Exact linearization and non-interacting control of a 4 rotors helicopter via dynamic feedback. In: 10th IEEE Int. Workshop on Robot–Human Interactive Communication. Paris (2001)
Bijnens, B., Chu, Q.P., Voorsluijs, G.M., Mulder, J.A.: Adaptive feedback linearization flight control for a helicopter UAV. In: AIAA Guidance, Navigation, and Control Conference and Exhibit. San Francisco, California (2005)
Altug, E., Ostrowski, J.P., Mahony, R.: Control of a quadrotor helicopter using visual feedback. In: IEEE International Conference on Robotics and Automation. Washington, DC (2002)
Cheng, M., Huzmezan, M.: A combined MBPC/2 DOF hinf controller for quad rotor unmanned air vehicle. In: AIAA Atmospheric Flight Mechanics Conference and Exhibit. Austin, Texas, USA (2003)
Cowling, I.D., Yakimenko, O.A., Whidborne, J.F., Cooke, A.K.: A prototype of an autonomous controller for a quadrotor UAV. In: Proceedings of the European Control Conference. Kos, Greece (2007)
Guo, W., Horn, J.: Modeling and simulation for the development of a quad-rotor UAV capable of indoor flight. In: Modeling and Simulation Technologies Conference and Exhibit. Keystone, Colorado (2006)
Mahony, R., Hamel, T., Dzul, A.: Hover control via lyapunov control for an autonomous model helicopter. In: Proceedings of the 38th Conference on Decision & Control. Phoenix, Arizona (1999)
Lewis, F.L., Dawson, D.M., Abdallah, C.T.: Robot Manipulator Control: Theory and Practices. Marcel Dekker, New York (2004)
Lewis, F., Jagannathan, S., Yesildirek, A.: Neural Network Control of Robot Manipulators and Nonlinear Systems. Taylor and Francis, London (1999)
Kim, Y.H., Lewis, F.L.: High Level Feedback Control With Neural Networks. World Scientific. River Edge, NJ (1998)
Olfati-Saber, R.: Nonlinear control of underactuated mechanical systems with application to robotics and aerospace vehicles. In: Doctor of Philosophy, Dept. of Electrical Engineering and Computer Science, p. 307. MIT (2001)
Hornik, K., Stinchombe, M., White, H.: Multilayer feedforward networks are universal approximations. Neural Netw. 20, 359–366 (1989). doi:10.1016/0893-6080(89)90020-8
Lewis, F.L., Yesildirek, A., Liu, K.: Multilayer neural-net robot controller with guaranteed tracking performance. IEEE Trans. Neural Netw. 7, 388–399 (1996). doi:10.1109/72.485674
Fantoni, I., Zavala, A., Lozano, R.: Global stabilization of a PVTOL aircraft with bounded thrust. In: Proceedings of the 41st Conference on Decision and Control. Las Vegas, Nevada USA (2002)
Lewis, F.L., Abdallah, C.T., Dawson, D.M.: Control of Robot Manipulators. Macmillan, New York (1993)
Flash, T., Hogan, N.: The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703 (1985)
Hogan, N.: Adaptive control of mechanical impedance by coactivation of antagonist muscles. IEEE Trans. Automat. Contr. 29, 681–690 (1984). doi:10.1109/TAC.1984.1103644
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Das, A., Lewis, F. & Subbarao, K. Backstepping Approach for Controlling a Quadrotor Using Lagrange Form Dynamics. J Intell Robot Syst 56, 127–151 (2009). https://doi.org/10.1007/s10846-009-9331-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10846-009-9331-0