Abstract
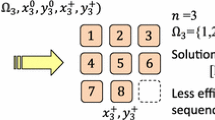
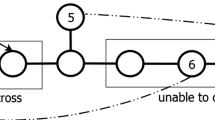
In the Box Push Planning problem, the aim is to find a path for a robot that transfers a movable object from an initial to a target position by merely pushing it. Due to the irreversibility of object movements, deadlocks are the main challenge in this problem, making it NP-complete and PSPACE-hard, even in discrete workspaces. While all our studied previous researches have addressed this problem for minimizing the number of box pushes, in this paper the objective function of the problem incorporates a combination of the movements of both the box and the pushing robot. Furthermore, a new method called Sequential Bi-criteria Search (SBS) has been proposed for solving the single-box push planning problem on grids. The SBS applies different cost criteria in two consecutive phases: first the path length of only the box from its initial to target positions is minimized, and then the overall objective function (which considers the robot’s movements as well) is minimized. The proposed method is optimal and complete, and experimental results showed that its search tree size and runtime are significantly less than both the standard and improved A* search. The properties of SBS are discussed in detail, and it is shown that it can be utilized to solve other constraint satisfaction problems, as well as multi-criteria optimization problems by sequentially relaxing its criteria and solving incremental subproblems through consecutive phases.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Ahmad, N., Agah, A.: Plan and intent recognition in a multi-agent system for collective box pushing. J. Intell. Syst. 23(1), 95–108 (2013)
Akella, S., Mason, M.T.: Posing polygonal objects in the plane by pushing. In: Proc. of IEEE Int. Conf. on Robotic and Automation, 2255–2262 (1992)
Barnhart, C., Johnson, E.L., Nemhauser, G.L., Savelsbergh, M.W.P., Vance, P.H.: Branch-and-Price: Column Generation for Huge Integer Programs. Oper. Res. 46, 316–329 (1998)
Ben-Shahar, O., Rivlin, E.: To push or not to push: On the rearrangement of movable objects by a mobile robot. In: Proc. of IEEE Int. Conf. on Robotic and Automation, 159–164 (1996)
Ben-Shahar, O., Rivlin, E.: To push or not to push: On the rearrangement of movable objects by a mobile robot. IEEE Trans. Syst. Man Cybern. B 28(5), 667–679 (1998)
Bremner, D., O’Rourke, J., Shermer, T: Motion planning amidst movable square blocks is PSPACE complete. Draft (1994)
Culberson, J.: Sokoban is PSPACE-complete. In: Proc. of the Int. Conf. on Fun with Algorithms, 65–76 (1998)
Demaine, E.D., Demaine, M.L., Hoffmann, M., O’Rourke, J.: Pushing blocks is hard. Comput. Geom. 26, 21–36 (2003)
Demaine, E.D., Hearn, R.A., Hoffmann, M.: Push-2-F is PSPACE-Complete. In: Proc. of the 14 th Canadian Conference on Computational Geometry, 31–35 (2002)
Demaine, E.D., Hoffmann, M.: Pushing blocks is NP-complete for noncrossing solution paths. In: Proc. 13th Canadian Conference on Computational Geometry, 65-68 (2001)
Demaine, E.D., Hoffmann, M., Holzer, M.: PushPush-k is PSPACE-Complete. In: Proc. 3rd Int. Conf. Fun with Algorithms (FUN ‘04), 159–170 (2004)
Demaine, E.D., Demaine, M.L., O’Rourke, J.: PushPush and Push-1 are NP-hard in 2D. In: Proc. of the 12th Canadian Conference on Computational Geometry, 211–219 (2000)
Dhagat, A., O’Rourke, J.: Motion planning amidst Movable Square blocks. In: Proc. of the 4 th Canadian Conference on Computational Geometry, 188-191 (1992)
Dor, D., Zwick, U.: SOKOBAN and other motion planning problems. Comput. Geom. 13, 215–228 (1999)
Friedman, E.: Pushing Blocks in Gravity is NP-hard, http://www.stetson.edu/~efriedma (2002)
Ghosh, A., Konar, A., Janarthanan, R.: Multi-robot cooperative box-pushing problem using multi-objective particle swarm optimization Technique. In: IEEE World Congress on Information and Communication Technologies (WICT), pp. 272–277 (2012)
Havur, G., Ozbilgin, G., Erdem, E., Patoglu, V.: Geometric rearrangement of multiple movable objects on cluttered surfaces: A hybrid reasoning approach. IEEE International Conference on Robotics and Automation, 445–452 (2014)
Hearn, R.A., Demaine, E.D.: PSPACE-completeness of sliding-block puzzles and other problems through the nondeterministic constraint logic model of computation. Theor. Comput. Sci. 343(1-2), 72–96 (2005)
Hoffmann, M.: Motion Planning Amidst Movable Square Blocks: Push-* is NP-hard. In: Proc. of the 12 th Canadian Conference on Computational Geometry, 205-210 (2000)
Jarvis, R.: Collision free trajectory planning using distance transforms, Mechanical Engineering Transactions. J. Inst. Eng. 10, 191–197 (1985)
Latombe, J.C.: Robot Motion Planning. Kluwer Academic Pub, London (1991)
Alami, R., Laumond, J.P., Siméon, T.: Two manipulation planning algorithms. In: Goldberg, K., et al (eds.) Algorithmic Foundations of Robotics, 109-125 (1995)
Laumond, J.P., Dacre-Wright, B., Alami, R.: Motion planning for a robot and a movable object amidst polygonal obstacle. Proc. of IEEE Int. Conf. on Robotic and Automation, 2474–2480 (1992)
Laumond, J.P., Simeon, T., Cortes, J., Sahbani, A.: A general manipulation task planner. In: WAFR, 293–309 (2002)
Levihn, M., Scholz, J., Stilman, M.: Planning with movable obstacles in continuous environments with uncertain dynamics. IEEE International Conference on Robotics and Automation, 3832–3838 (2013)
Levihn, M., Stilman, M., Christensen, H.: Locally Optimal Navigation among Movable Obstacles in Unknown Environments. In: International Conference on Humanoid Robots (2014)
Lindzey, L., Knepper, R., Choset, H., Srinivasa, S. Algorithmic Foundations of Robotics XI (107), 301 (2015)
Lynch, K.M., Mason, M.T.: Stable Planning: Mechanics, Controllability, and Planning. Int. J. Robot. Res. 15(6), 533–556 (1996)
Moghaddam, K.M., Masehian, E.: Planning Robot Navigation Among Movable Obstacles (NAMO) Through A Recursive Approach. J. Intell. Robot. Syst. (2016). doi:10.1007/s10846-016-0344-1
O’Rourke, J.: The Smith Problem Solving Group (1999), PushPush is NP-hard in 3D, Smith Technical Report 064
Ota, J.: Rearrangement of multiple movable objects: Integration of global and local planning methodology. In: Proc. of IEEE Int. Conf. on Robotic and Automation, 1962–1967 (2004)
Oyama, N., Liu, Z., Gueta, L. B., Ota, J.: Task apportionment in a rearrangement problem of multiple mobile robots. Adv. Robot. 27(2), 93–107 (2013)
Parra-Gonzalez E.F., Ramírez-Torres, J.G.: Object Path Planner for the Box Pushing Problem. In: Yasuda, T. (ed.) Multi-Robot Systems, Trends and Development, InTech Pub., pp. 291-306 (2011)
Pereira, A.G., Ritt, M., Buriol, L.S.: Finding Optimal Solutions to Sokoban Using Instance Dependent Pattern Databases. In: Proc. of the Sixth International Symposium on Combinatorial Search, 141–148 (2013)
Ritt, M.: Motion planning with pull moves, available online at 1008.2952 (2010)
Russell, S.J., Norvig, P.: Artificial Intelligence A Modern Approach, 3rd edn. Prentice Hall (2010)
Stilman, M., Kuffner, J.J.: Planning among movable obstacles with artificial constraints. In: Proc. 6 th Int. Workshop on the Algorithmic Foundations of Robotics, 1–20 (2006)
Wilfong, G.: Motion planning in the presence of movable obstacles. In: ACM Symp Computational Geometry, 279–288 (1988)
Wu, H., Levihn, N.M., Stilman, M.: Navigation Among Movable Obstacles in Unknown Environments. In: Proc IEEE International Conference on Intelligent Robots and Systems (IROS), 1433–1438 (2010)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Masehian, E., Morovati, R. A Sequential Bi-criteria Search Algorithm for Robot Path Planning in the Box Pushing Problem. J Intell Robot Syst 86, 523–550 (2017). https://doi.org/10.1007/s10846-016-0424-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10846-016-0424-2