Skip to main content

Advertisement

Springer Nature Link
Log in

Sensitivity Analysis and Model Validation of a 2-DoF Mini Spherical Robot

  • Published:
Journal of Intelligent & Robotic Systems Aims and scope Submit manuscript

Abstract

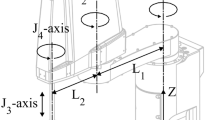
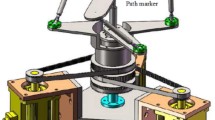
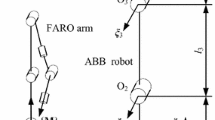
This paper is focused on the development and validation of an error kinematic model of a mini spherical robot, aimed at its kinematic calibration. The robot is actually a spatial five-bar linkage, provided with two rotational degrees of freedom. A non-overconstrained kinematics is assumed for the robot in order to provide a simple mathematical model and allow a sensitivity analysis of all the involved geometric parameters. A simplified version of the model is proposed. It differs only for the degree of approximation. A comparison between full and reduced models is presented by means of numerical simulations, analyzing their behavior in a significant region of the robot workspace. In order to validate both of them a robot calibration is carried out on a physical prototype of the robot using a vision system, namely a fixed camera in a eye-to-hand configuration. An iterative algorithm aimed at the experimental identification of the geometric data of the robot is used. Some experimental results show the effectiveness of the study.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Abtahi, M., Pendar, H., Alasty, A., Vossoughi, G.: Experimental kinematic calibration of parallel manipulators using a relative position error measurement system. Robot. Comput. Integr. Manuf. 26(6), 799–804 (2010)

    Article  Google Scholar 

  2. Fassi, I., Legnani, G.: Hand to sensor calibration: A geometrical interpretation of the matrix equation AX=XB. J. Robot. Syst. 22(9), 497–506 (2005)

    Article  MATH  Google Scholar 

  3. Gojtan, G., Furtado, G., Hess-Coelho, T.: Error analysis of a 3-dof parallel mechanism for milling applications. ASME J. Mech. Robot 5(3), 034,501 (9 pages) (2013)

    Article  Google Scholar 

  4. Gonzalez-Hernandez, A., Castillo-Castaneda, E.: Stiffness estimation of a parallel manipulator using image analysis and camera calibration techniques. Robotica 31(4), 657–667 (2013)

    Article  Google Scholar 

  5. Gosselin, C., Caron, F.: Two degree-of-freedom spherical orienting device. Google Patents, https://www.google.ch/patents/US5966991. US Patent n∘5,966,991 (1999)

  6. Heikkila, J., Silven, O.: A four-step camera calibration procedure with implicit image correction. In: Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 1106–1112. San Juan, Puerto Rico (1997)

  7. Hollerbach, J.M., Wampler, C.W.: The calibration index and taxonomy for robot kinematic calibration methods. Int. J. Robot. Res. 15(6), 573–591 (1996)

    Article  Google Scholar 

  8. Huang, T., Chetwynd, D.G., Mei, J.P., Zhao, X.M.: Tolerance design of a 2-dof overconstrained translational parallel robot. IEEE Trans. Robot. 22(1), 167–172 (2006)

    Article  Google Scholar 

  9. Jin, Y., Chen, I.M.: Effects of constraint errors on parallel manipulators with decoupled motion. Mech. Mach. Theory 41(8), 912–928 (2006)

    Article  MATH  Google Scholar 

  10. Kim, H.: Kinematic calibration of a cartesian parallel manipulator. Int. J. Control Autom. Syst. 3(3), 453–460 (2005)

    Google Scholar 

  11. Legnani, G., Tosi, D., Adamini, R., Fassi, I.: Calibration of parallel kinematic machines: theory and applications, industrial robotics: programming, simulation and applications. In: Huat, L.K. (ed.) InTech (2006)

  12. Liu, H., Huang, T., Chetwynd, D.G.: A general approach for geometric error modeling of lower mobility parallel manipulators. J. Mech. Robot. 3(2), 0210,131 (13 page) (2011)

    Article  Google Scholar 

  13. Meng, J., Li, Z.: A general approach for accuracy analysis of parallel manipulators with joint clearance. In: 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2468–2473. Edmonton, Alberta (2005)

  14. Merlet, J.P.: Interval analysis for certified numerical solution of problems in robotics. Int. J. Appl. Math. Comput. Sci. 19, 399–412 (2009)

    Article  MATH  Google Scholar 

  15. Mooring, B., Roth, Z.S., Driels, M.R.: Fundamentals of Manipulator Calibration. Wiley, New York (1991)

    Google Scholar 

  16. Palmieri, G.: On the positioning error of a 2-dof spherical parallel wrist with flexible links and joints - an fem approach. Mech. Sci. 6, 9–14 (2015)

    Article  Google Scholar 

  17. Palmieri, G., Callegari, M., Carbonari, L., Palpacelli, M.C.: Mechanical design of a mini pointing device for a robotic assembly cell. Meccanica 50(7), 1895–1908 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Palpacelli, M.C., Palmieri, G., Carbonari, L., Corinaldi, D.: Sensitivity analysis of a mini pointing device. In: Proceedings of MESA 2016 - 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications. Auckland, New Zealand (2016)

  19. Park, F.C., Okamura, K.: Kinematic Calibration and the Product of Exponentials Formula, pp. 119–128. Springer, Dordrecht (1994)

    Google Scholar 

  20. Pashkevich, A., Chablat, D., Wenger, P.: Stiffness analysis of overconstrained parallel manipulators. Mech. Mach. Theory 44(5), 966–982 (2009)

    Article  MATH  Google Scholar 

  21. Ramesh, R., Mannan, M., Poo, A.: Error compensation in machine tools a review: part i: geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 40(9), 1235–1256 (2000)

    Article  Google Scholar 

  22. Rao, S., Bhatti, P.: Probabilistic approach to manipulator kinematics and dynamics. Reliab. Eng. Syst. Safety 72(1), 47–58 (2001)

    Article  Google Scholar 

  23. Rauf, A., Kim, S.G., Ryu, J.: Complete parameter identification of parallel manipulators with partial pose information using a new measurement device. Robotica 22(6), 689–695 (2004)

    Article  Google Scholar 

  24. Renaud, P., Andreff, N., Martinet, P., Gogu, G.: Kinematic calibration of parallel mechanisms: A novel approach using legs observation. IEEE Trans. Robot. 21(4), 529–538 (2005)

    Article  Google Scholar 

  25. Sun, T., Zhai, Y., Song, Y., Zhang, J.: Kinematic calibration of a 3-dof rotational parallel manipulator using laser tracker. Robot. Comput.-Integr. Manuf. 41, 78–91 (2016)

    Article  Google Scholar 

  26. Tannous, M., Caro, S., Goldsztejn, A.: Sensitivity analysis of parallel manipulators using an interval linearization method. Mech. Mach. Theory 71, 93–114 (2014)

    Article  Google Scholar 

  27. Traslosheros, A., Sebastián, J.M., Torrijos, J., Carelli, R., Castillo, E.: An inexpensive method for kinematic calibration of a parallel robot by using one hand-held camera as main sensor. Sensors 13, 9941–9965 (2013)

    Article  Google Scholar 

  28. Vivas, A., Poignet, P., Marquet, F., Pierrot, F., Gautier, M.: Experimental dynamic identification of a fully parallel robot. In: 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), vol. 3, pp. 3278–3283. Taipei, Taiwan (2003)

  29. Wang, S., Ehmann, K.: Error model and accuracy analysis of a six-dof stewart platform. ASME J. Manuf. Sci. Eng. 124(2), 286–295 (2002)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. DIISM, Polytechnic University of Marche, Ancona, (AN), Italy

    Matteo Palpacelli, Giacomo Palmieri, Luca Carbonari & David Corinaldi

Authors
  1. Matteo Palpacelli
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Giacomo Palmieri
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Luca Carbonari
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. David Corinaldi
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Matteo Palpacelli.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Palpacelli, M., Palmieri, G., Carbonari, L. et al. Sensitivity Analysis and Model Validation of a 2-DoF Mini Spherical Robot. J Intell Robot Syst 91, 155–163 (2018). https://doi.org/10.1007/s10846-017-0679-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10846-017-0679-2

Keywords