Path Following Control of Quadrotor UAV With Continuous Fractional-Order Super Twisting Sliding Mode

Abstract

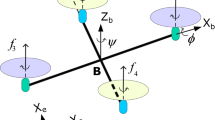
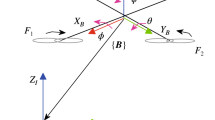
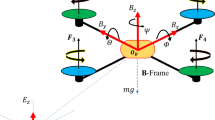
Quadrotors are highly maneuverable drones, which are susceptible to the parameter uncertainties such as the mass, drag coefficients, and moment of inertia. Whose nonlinearities, aerodynamic disturbances, and higher coupling between the rotational and the translational dynamics stand for a problem that demands a robust controller. In the present paper, a fractional order (FO) improved super twisting proportional-integral-derivative sliding-mode control (STPIDSMC) is proposed for the quadrotor system. To improve the speed tracking performance, a FOPIDSM surface is designed. Moreover, the proposed FO control approach ensures fast convergence, high precision, good robustness against stochastic perturbations and uncertainties. Finally, the performance of the FOSTPIDSMC is investigated under different scenarios. The simulation results clearly show the high control performance, efficiency and high disturbance rejection capacity of the controller strategy proposed in this work in comparison with the nonlinear internal model control (NLIMC) and FO backstepping sliding mode control (FOBSMC) strategies.

Appendix

The Super-Twisting Algorithm (STA) with a perturbation is defined by the following equation as [66, 67].

Proof

To proof the stability of the system, the standard Super-Twisting Algorithm (STA) with a perturbation is defined as [66, 67]:

$$ \begin{array}{@{}rcl@{}} \dot{\Upsilon}_{1} &= &-b_{1} \vert {\Upsilon}_{1} \vert^{\frac{1}{2}}sign({\Upsilon}_{1})+{\Upsilon}_{2}\\ \dot{\Upsilon}_{2} &= &-b_{2} sign({\Upsilon}_{1})+d({\Upsilon},t) \end{array} $$

(52)

The term ${\Upsilon }_{1} \in \mathbb {R}$ and ${\Upsilon }_{2}\in \mathbb {R}$ denote the state variables, $b_{1}\in \mathbb {R^{+}}$, $b_{2}\in \mathbb {R^{+}}$ and d(t, ϒ) is a perturbation term bounded as (d(t,ϒ) < D). Define the Lyapunov function presented in [66, 67] as

$$ V({\Upsilon})= \zeta^{T} P_{ST} \zeta $$

(53)

with $\zeta =[\vert {\Upsilon }_{1} \vert ^{\frac {1}{2}}sign({\Upsilon }_{1}),{\Upsilon }_{2}]$ and P = P^T is a non-negative matrix, which is a solution of an algebraic Lyapunov equation defined in Eq. 54.

$$ A_{ST}^{T} P_{ST}+A_{ST} P_{ST}= -Q_{ST} $$

(54)

with $Q_{ST}=Q_{ST}^{T}>0$ and A_ST is Hurwitz, define in Eq. 55

$$ \begin{bmatrix} -\frac{1}{2}b_{1} & \ \ \ \ \ \frac{1}{2}\\ -b_{2} & \ \ \ \ \ 0 \end{bmatrix} $$

(55)

Moroever, the derivative of $\dot {V}$ respect to time presented in [66, 67] satisfies the

$$ \dot{V}\leq -\gamma(Q_{ST})V^{\frac{1}{2}}({\Upsilon}) $$

(56)

where

$$ \gamma(Q_{ST}) \triangleq \frac{{\Pi}_{min}(Q_{ST}){\Pi}_{min}^{\frac{1}{2}}(P_{ST})}{{\Pi}_{max}(P)} $$

(57)

is a scalar depending on the selection of the matrix Q_ST. □