Abstract
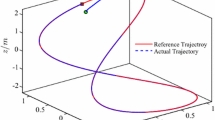
The aim of this study is to develop robust guidance laws for the control motion of an underwater autonomous vehicle (UAV) in a three-dimensional (3D) space. The control design is based on the use of Averaged Sub-Gradient (ASG) version of a class of dynamic integral sliding mode (ISM) method being sequentially applied to the subsystems of the complete model realizing, the so-called backstepping (or cascade) approach. The mathematical form of the UAV model induces a backstepping formulation for solving the tracking trajectory problem sequentially for the position, translation velocity, angular velocity and actuators (thrusters) dynamics. The solution of the trajectory tracking problem at each stage implements the ASG-version of the ISM method. This problem is treated as the optimization of a suitable convex (not obligatory strongly convex) cost functional, depending on the tracking error and reaching its minimal value at the origin of the error tracking space. This study shows that the minimization of the proposed functional leads to the optimal tracking regime under the presence of uncertainties in the mathematical model description. A numerical example proves the effectiveness of the suggested robust dynamic controller. The comparison between the obtained trajectory tracking results and the outcomes produced by a set of standard proportional integral derivative (PID) controllers, is presented. The proposed controller exhibits a better tracking of the reference trajectory compared with the PID version, showing a smaller mean square estimation for the tracking error.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Code Availability
The software used for developing the numerical evaluations is available upon direct request to the corresponding author.
References
González-García, J., Gómez-Espinosa, A., Cuan-Urquizo, E., García-Valdovinos, L.G., Salgado-Jiménez, T., Cabello, J.A.E.: Autonomous underwater vehicles: Localization, navigation, and communication for collaborative missions. Appl. Sci. 10, 1256 (2020)
Martínez, N.L., Martínez-Ortega, J.F., Rodríguez-Molina, J., Zhai, Z.: Proposal of an automated mission manager for cooperative autonomous underwater vehicles. Appl. Sci. 10(3), 855 (2020)
Wynn, R.B., Huvenne, V.A., Le Bas, T.P., Murton, B.J., Connelly, D.P., Bett, B.J., Ruhl, H.A., Morris, K.J., Peakall, J., Parsons, D.R., et al.: Autonomous underwater vehicles (auvs): Their past, present and future contributions to the advancement of marine geoscience. Mar. Geol. 352, 451–468 (2014)
Fernandes, P.G., Stevenson, P., Brierley, A.S., Armstrong, F., Simmonds, E.J.: Autonomous underwater vehicles: Future platforms for sheries acoustics. ICES J. Mar. Sci. 60(3), 684–691 (2003)
Bingham, D., Drake, T., Hill, A., Lott, R.: The application of autonomous underwater vehicle (auv) technology in the oil industry vision and experiences. In: FIG XXII International Congress Washington, DC USA, pp 19–26 (2002)
Iscar Ruland, E.A.: Low-cost vision based autonomous underwater vehicle for abyssal ocean ecosystem research. Ph.D dissertation (2020)
Breivik, M., Fossen, T.I.: Guidance laws for autonomous underwater vehicles. Underwater vehicles. pp. 51–76 (2009)
Breivik, M., Fossen, T.I.: Guidance-based path following for autonomous underwater vehicles. In: Proceedings of OCEANS 2005 MTS/IEEE, pp 2807–2814. IEEE (2005)
Xiang, X., Yu, C., Zhang, Q.: Robust fuzzy 3d path following for autonomous underwater vehicle subject to uncertainties. Comput. Operat. Res. 84, 165–177 (2017)
Encarnacao, P., Pascoal, A.: 3d path following for autonomous underwater vehicle. In: Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No. 00CH37187), vol. 3, pp 2977–2982. IEEE (2000)
Chu, Z., Zhu, D.: 3d path-following control for autonomous underwater vehicle based on adaptive backstepping sliding mode. In: 2015 IEEE International Conference on Information and Automation, pp 1143–1147. IEEE (2015)
Xie, T., Li, Y., Jiang, Y., An, L., Wu, H.: Backstepping active disturbance rejection control for trajectory tracking of underactuated autonomous underwater vehicles with position error constraint. Int. J. Adv. Robot. Syst. 17(2), 1729881420909633 (2020)
Cho, G.R., Li, J.H., Park, D., Jung, J.H.: Robust trajectory tracking of autonomous underwater vehicles using back-stepping control and time delay estimation. Ocean Eng. 201, 107131 (2020)
Liu, X., Zhang, M., Wang, S.: Adaptive region tracking control with prescribed transient performance for autonomous underwater vehicle with thruster fault. Ocean Eng. 196, 106804 (2020)
Bu, X.: Air-breathing hypersonic vehicles funnel control using neural approximation of non-a neural dynamics. IEEE/ASME Transactions On Mechatronics 23(5), 2099 (2018)
Bu, X., Qi, Q.: Fuzzy optimal tracking control of hypersonic flight vehicles via single-network adaptive critic design. IEEE Transactions on Fuzzy Systems (2020)
Poznyak, A., Nazin, A., Alazki, H.: Integral sliding mode convex optimization in uncertain lagrangian systems driven by PMDC motors: averaged subgradient approach. IEEE Transactions on Automatic Control (2021)
Utkin, V., Poznyak, A., Orlov, Y., Polyakov, A.: Road Map for Sliding Mode Control Design. SpringerBriefs in Mathematics. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-41709-3
Fossen, T.I., et al.: Guidance and Control of Ocean Vehicles, vol. 199. Wiley, New York (1994)
Shahgholian, G., Shafaghi, P.: State space modeling and eigenvalue analysis of the permanent magnet dc motor drive system. In: 2010 2nd International Conference on Electronic Computer Technology, pp 63–67. IEEE (2010)
Kokotovic, P.: The joy of feedback: nonlinear and adaptive. IEEE Control Systems Magazine 12 (3), 7-17 (1992). https://doi.org/10.1109/37.165507
Lozano, R., Brogliato, B.: Adaptive control of robot manipulators with flexible joints. IEEE Trans. Autom. Control 37(2), 174 (1992). https://doi.org/10.1109/9.121619
Khalil, H.K., Grizzle, J.W.: Nonlinear systems, vol. 3. Prentice hall Upper Saddle River, NJ (2002)
Levant, A.: Sliding order and sliding accuracy in sliding mode control. Int. J. Control 58(6), 1247-1263 (1993)
Levant, A.: Robust exact differentiation via sliding mode technique. Automatica 34(3), 379-384 (1998)
da Silva, J.E., Terra, B., Martins, R., de Sousa, J.B.: Modeling and simulation of the lauv autonomous underwater vehicle.. In: 13th IEEE IFAC International Conference on Methods and Models in Automation and Robotics, vol. 1. Szczecin, Poland (2007)
Utkin, V., Guldner, J., Shijun, M.: Sliding mode control in electro-mechanical systems, vol. 34, CRC Press (1999)
Acknowledgments
The paper was prepared within of the Program of creation and development of the world-class research center Sverhzvuk in 2020-2025 under financial support of the Ministry of Science and Higher Education of the Russian Federation (Order of the Government of the Russian Federation dated 24 October 2020 N 2744-p)
Funding
The paper was prepared within of the Program of creation and development of the world-class research center Sverhzvuk in 2020-2025 under financial support of the Ministry of Science and Higher Education of the Russian Federation (Order of the Government of the Russian Federation dated 24 October 2020 N 2744-p).
Author information
Authors and Affiliations
Contributions
AHS has developed the theoretical analysis and the numerical simulations; IC has supervised the theoretical development; AP has proposed the theoretical fundamentals of this study as well as manuscript writing and OA has contributed the numerical study as well as manuscript writing.
Corresponding author
Ethics declarations
Ethics approval
All the developed results presented in this study have been conducted under the most strict ethical guidelines.
Consent to participate
All authors participated in the development of both theoretical and simulated outcomes.
Consent for Publication
All authors consent to publish this study.
Conflict of Interests
The authors have not conflict of interest to declare.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Availability of data and material
The software used for developing the numerical evaluations is available upon direct request to the corresponding author.
Appendix
Appendix
Proof Proof of Theorem 1
To prove that the designed pseudo-controllers my solve the proposed optimization problems, let consider the following general equivalent stabilization problem.
-
a) Consider the Lyapunov function
$$ V(\mathbf{s})=\frac{1}{2}\left\Vert \mathbf{s}\right\Vert^{2},\text{ }\rho >0, $$(48)Taking then s := s1, we get
$$ \left. \begin{array}{c} \dot{V}(\mathbf{s}_{1})=\mathbf{s}_{1}^{\top }\dot{\mathbf{s}}_{1}= \mathbf{s}_{1}^{\top }\left[ \ddot{\mathbf{\varphi}}_{1}+\frac{\dot{\mathbf{ \varphi}}_{1}}{t+\kappa }-\frac{\mathbf{\varphi }_{1}+\mathbf{\alpha } _{1}}{\left( t+\kappa \right)^{2}}-\frac{1}{t+\kappa }\mathbf{\Gamma }_{1}+ \frac{1}{t+\kappa }\partial J_{\mathbf{1}}(\mathbf{\varphi }_{1})\right] \\ =\mathbf{s}_{1}^{\top }\left[ \ddot{\mathbf{{\varkappa}}}-\ddot{{\varkappa}}^{\ast }+\frac{\dot{\mathbf{{\varkappa}}}-\dot{{\varkappa}}^{\ast }}{t+\kappa }- \frac{\mathbf{{\varkappa} -{\varkappa} }^{\ast }+\mathbf{\alpha }_{1}}{\left( t+\kappa \right)^{2}}-\frac{1}{t+\kappa }\mathbf{\Gamma }_{1}+\frac{1}{ t+\kappa }\partial J_{\mathbf{1}}(\mathbf{\varphi }_{1})\right] \\ =\mathbf{s}_{1}^{\top }\left[ \frac{d}{dt}\left( {{\varTheta}} \mathbf{u} _{1}^{\ast }\right) +\dot{\mathbf{\zeta}}_{\mathbf{{\varkappa} }}+\mathbf{g} _{1}\right] . \end{array} \right\} $$(2)Select the intermediate pseudo-control \(\mathbf {\upsilon =u}_{1}^{\ast }\) satisfying (17). Then from (2) we get
$$ \left. \begin{array}{c} \dot{V}(\mathbf{s}_{1})=\mathbf{s}_{1}^{\top }\left[ -k_{1}\text{sign} \left( \mathbf{s}_{1}\right) +\dot{\mathbf{\zeta}}_{\mathbf{{\varkappa} }} \right] \leq \left( -k_{1}\sum\limits_{i=1}^{3}\left\vert s_{1,i}\right\vert +\left\Vert \mathbf{s}_{1}\right\Vert \dot{\zeta}_{ \mathbf{{\varkappa} }}^{+}\right) \\ \leq \left\Vert \mathbf{s}_{1}\right\Vert \left( -k_{1}+\dot{\zeta}_{\mathbf{ {\varkappa} }}^{+}\right) =-\mathring{\rho}\left\Vert \mathbf{s} _{1}\right\Vert =-\mathring{\rho}\sqrt{2V(\mathbf{s}_{1})}, \end{array} \right\} $$which leads to the following relations
$$ \left. \begin{array}{c} \frac{dV(\mathbf{s}_{1})}{\sqrt{V(\mathbf{s}_{1})}}\leq -\mathring{\rho} \sqrt{2}dt\rightarrow 2\left( \sqrt{V(\mathbf{s}_{1})}-\sqrt{V(\mathbf{s} _{1}(0))}\right) \leq -\mathring{\rho}\sqrt{2}t, \\ 0\leq \sqrt{V(\mathbf{s}_{1})}\leq \sqrt{V(\mathbf{s}_{1}(0))}-\frac{ \mathring{\rho}}{\sqrt{2}}t, \end{array} \right\} $$implying that \(V(\mathbf {s}_{1}\left (t\right ) )=0\) for all
$$ t\geq t_{reach}:=\frac{1}{\mathring{\rho}}\sqrt{2V(\mathbf{s}_{1}(0))}= \frac{\left\Vert \mathbf{s}_{1}\left( 0\right) \right\Vert }{\mathring{\rho} }. $$(3)But by (20), \(\mathbf {s}_{1}\left (0\right ) =\mathbf {0}\), and hence from the beginning of the process
$$ \mathbf{s}_{1}\left( t\right) =\dot{\mathbf{s}}_{1}\left( t\right) =\mathbf{0 }. $$(4) -
b) Let now show that the robust controller (17), (19), (20), providing property (4), solves the optimization problem (16) as in (21). Indeed, following [17] and defining μ(t) := t + κ, we represent (4) as
$$ \begin{array}{@{}rcl@{}} \mu (t)\mathbf{s}_{1}&=&\mu (t)\dot{\mathbf{\varphi}}_{1}(t)+\mathbf{\varphi } _{1}(t)+\mathbf{\alpha }_{1}+\mathbf{\gamma }(t)=0,\\&&\text{ }\dot{\mathbf{ \gamma}}(t)=\partial J_{\mathbf{1}}(\mathbf{\varphi }_{1}(t)),\text{ } \mathbf{\gamma }(0)=0, \end{array} $$or, equivalently,
$$ \mu (t)\dot{\mathbf{\varphi}}_{1}(t)+\mathbf{\varphi }_{1}(t)+\mathbf{\alpha }_{1}=-\mathbf{\gamma }(t), $$which gives
$$ \begin{array}{c} \frac{d}{dt}\left[ \frac{1}{2}\left\Vert \mathbf{\gamma }\right\Vert^{2} \right] =\dot{\mathbf{\gamma}}^{\top }\mathbf{\gamma }=-\partial^{\top }J_{\mathbf{1}}(\mathbf{\varphi }_{1})\left[ \mu \dot{\mathbf{ \varphi}}_{1}+\mathbf{\varphi }_{1}+\mathbf{\alpha }_{1}\right] \\ =-\partial^{\top }J_{\mathbf{1}}(\mathbf{\varphi }_{1})\mathbf{\varphi }_{1}-\partial^{\top }J_{\mathbf{1}}(\mathbf{\varphi }_{1})\left( \mu \dot{\mathbf{\varphi}}_{1}+\mathbf{\alpha }_{1}\right) . \end{array} $$
Applying the inequality
to the first term in the right-hand side and using the identity
we have
Then, integrating this inequality on interval \(\left [ 0,t\right ] \), we get
Since \(\dot {\mu }_{\tau }=1\), in the last inequality leads (using of the integration by parts) we have
which leads to
or equivalently,
that gives (22). Theorem is proven. □
Proof Proof of Theorem 2
and then the proof exactly follows the proof of Theorem 1. □
Proof Proof of Theorem 3
and then the proof follows the proof of Theorem 1. □
Proof Proof of Theorem 4
and then the proof follows the proof of Theorem 1. □
Rights and permissions
About this article
Cite this article
Hernandez-Sanchez, A., Chairez, I., Poznyak, A. et al. Dynamic Motion Backstepping Control of Underwater Autonomous Vehicle Based on Averaged Sub-gradient Integral Sliding Mode Method. J Intell Robot Syst 103, 48 (2021). https://doi.org/10.1007/s10846-021-01466-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10846-021-01466-3