Terminal Sliding Mode Control for Quadrotors with Chattering Reduction and Disturbances Estimator: Theory and Application

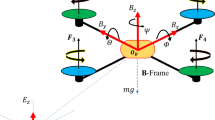
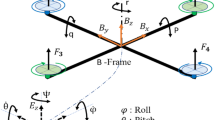
Abstract

This paper deals with the robust flight control problem of quadrotor while taking various model uncertainties and external disturbances into consideration. The novel flight controller is proposed based on the chattering reduced terminal sliding mode control method and a universal nonlinear disturbance estimator (NDE), which is applied to improve the robustness of the flight system. By skillfully using Lyapunov theory, the stability condition of the closed-loop systems is derived and it is shown that the control gains can be reduced by estimating the model uncertainties and external disturbances. Finally, compared with traditional methods, the theoretical results are validated experimentally through tests using a quadrotor assembled with PX4 and Pixracer. Two different kinds of model uncertainties and external disturbances cases, including partial failure of a rotor and the sudden change of the load, are validated through experiments. Since the nonlinear disturbance estimator is designed in a universal way, the proposed method shows great robustness in the above two different experiment cases without changing the structure of the flight controller and the nonlinear disturbance estimator.

Appendix A: Conversion relationship between the rotation matrix and quaternion

For the rotation matrix around x − y − z axises expressing as the following equation:

$$R = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\text{C}}\theta {\text{C}}\psi }&{{\text{S}}\phi {\text{S}}\theta {\text{C}}\psi - {\text{C}}\phi {\text{S}}\psi }&{{\text{C}}\phi {\text{S}}\theta {\text{C}}\psi + {\text{S}}\phi {\text{S}}\psi }\\ {{\text{C}}\theta {\text{S}}\psi }&{{\text{S}}\phi {\text{S}}\theta {\text{S}}\psi + {\text{C}}\phi {\text{C}}\psi }&{{\text{C}}\phi {\text{S}}\theta {\text{S}}\psi - {\text{S}}\phi {\text{C}}\psi }\\ { - {\text{S}}\theta }&{{\text{S}}\phi {\text{C}}\theta }&{{\text{C}}\phi {\text{C}}\theta } \end{array}} \right]$$

(A.1)

the corresponding quaternion can be computed in the following method.

If 1 + tr(R) > 0, then:

$$\begin{array}{@{}rcl@{}} {q_{0}} &=& \frac{{\sqrt{1 + {r_{11}} + {r_{22}} + {r_{33}}}}}{2}\\ {q_{1}} &=& \frac{{r_{32}} - {r_{23}}}{4{q_{0}}}\\ {q_{2}} &=& \frac{{r_{13}} - {r_{31}}}{4{q_{0}}}\\ {q_{3}} &=& \frac{{r_{21}} - {r_{12}}}{4{q_{0}}} \end{array}$$

(A.2)

If tr(R) →− 1 and ${\max \limits } \{ {r_{11}},{r_{22}},{r_{33}}\} = {r_{11}}$, then:

$$\begin{array}{@{}rcl@{}} t &=& \sqrt{1 + r_{11} - r_{22} - r_{33}}\\ {q_{0}} &=& \frac{{{r_{32}} - {r_{23}}}}{t}\\ {q_{1}} &=& \frac{t}{4}\\ {q_{2}} &=& \frac{{{r_{13}} + {r_{31}}}}{t}\\ {q_{3}} &=& \frac{{{r_{12}} + {r_{21}}}}{t} \end{array}$$

(A.3)

If tr(R) →− 1 and ${\max \limits } \{ {r_{11}},{r_{22}},{r_{33}}\} = {r_{22}}$, then:

$$\begin{array}{@{}rcl@{}} t &=& \sqrt {1 - {r_{11}} + {r_{22}} - {r_{33}}}\\ {q_{0}} &=& \frac{{{r_{13}} - {r_{31}}}}{t}\\ {q_{1}} &=& \frac{{{r_{12}} + {r_{21}}}}{t}\\ {q_{2}} &=& \frac{t}{4}\\ {q_{3}} &=& \frac{{{r_{32}} + {r_{23}}}}{t} \end{array}$$

(A.4)

If tr(R) →− 1 and ${\max \limits } \{ {r_{11}},{r_{22}},{r_{33}}\} = {r_{33}}$, then:

$$\begin{array}{@{}rcl@{}} t &=& \sqrt{1 - {r_{11}} - {r_{22}} + {r_{33}}}\\ {q_{0}} &=& \frac{{{r_{21}} - {r_{12}}}}{t}\\ {q_{1}} &=& \frac{{{r_{13}} + {r_{31}}}}{t}\\ {q_{2}} &=& \frac{{{r_{23}} - {r_{32}}}}{t}\\ {q_{3}} &=& \frac{t}{4} \end{array}$$

(A.5)