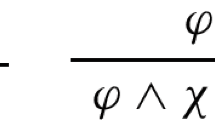Abstract
Recently, in an ongoing debate about informal provability, non-deterministic logics of informal provability BAT and CABAT were developed to model the notion. CABAT logic is defined as an extension of BAT logics and itself does not have independent and decent semantics. The aim of the paper is to show that, semantically speaking, both logics are rather complex and they can be characterized by neither finitely many valued deterministic semantics nor possible word semantics including neighbourhood semantics.
Similar content being viewed by others
Notes
For clarity, note that it’s possible to add the reflection principle for a formal provability predicate of a certain formal theory \(\mathbf {T}\). What we meant here is that it is impossible to have a provability predicate that shares the standard conditions put on formal provability and the reflection schema at the same time. In the first scenario the new predicate enriched by the reflection schema is no longer a formal provability predicate of the enriched theory.
To be fair if we add to the premise set a formula \(\mathtt {B}\lnot \lambda \rightarrow \lnot \lambda \) then the consequence does hold. But we are not interested here in an arbitraty instance of the reflection schema but in the translation of the standard proof of Löb’s theorem. Thus, in general the reflection schema is not assumed.
The etymology of the name CABAT is a bit more complex. “C” in the name stands for the closure condition and “A” for algebraic conditions that turned out to be redundant.
For the first interpretation, it’s impossible since the status of a mathematical claim may change. For instance, currently the Goldbach hypothesis is undecidable but it may turn out later that we will be able to prove or disprove it. Thus, a conjuction and disjuction of two independent sentences may turn out to be provable, refutable or remain undecided.
To be fair, it is also a perfectly viable motivation to approach informal provability from supervaluationistic perspective. This approach and the comparison between the two approaches, however, is beyond the scope of this paper.
On the other hand, it is an interesting system to study since it is a starting point and the system on top of which CABAT is defined.
Since BAT does not have any tautologies, we have to stick to its consequence relation.
From the fact that CABAT understood as the set of tautologies cannot have a finite many-valued characterization, it follows that CABAT understood as a consequence relation cannot have deterministic n valued semantics as well.
A non-normal Kripke semantics may contain non-normal worlds, resulting in the weakening of (Nec) [if \(\vdash \varphi \) then \(\vdash \Box \varphi \)] Chellas (1980).
For more information on this semantics see Chellas (1980).
Let F be a family of frames. We say that \(\varphi \) is a global semantic consequence of \(\Gamma \) (\(\Gamma \models \varphi \)) iff for all frames \(G\in F\), if \(G \models \Gamma \) then \(G\models \varphi \). For more details about this distinction see Chapter 1 of Blackburn (2001).
References
Antonutti Marfori, M. (2010). Informal proofs and mathematical rigour. Studia Logica, 96, 261–272.
Avron, A., & Zamanski, A. (2011). Non-deterministic semantics for logical systems. In Gabbay, & Guenthner, (Eds.), Handbook of philosophical logic, (Vol 160). Springer.
Avron, A., & Lev, I. (2001). Canonical propositional gentzen-type systems. In Automated reasoning: first international joint conference, IJCAR 2001 Siena, Italy, June 18-23, 2001 Proceedings (Lecture Notes in Computer Science), (pp. 529–544). Springer-Verlag.
Avron, A., & Lev, I. (2005). Non-deterministic multiple-valued structures. Journal of Logic and Computation, 15(3), 241–261.
Blackburn, P. (2001). Modal logic. Cambridge University Press.
Chellas, B. (1980). Modal logicÃ: an introduction. Cambridge University Press.
Coniglio, M. E., & Peron, N. M. (2014). Dugundji’s theorem revisited. Logica Universalis, 8(3–4), 407–422.
Dugundji, J. (1940). Note on a property of matrices for lewis and langford’s calculi of propositions. Journal of Symbolic Logic, 5(4), 150–151.
Goodman, N. D. (1984). Epistemic arithmetic is a conservative extension of intuitionistic arithmetic. Journal of Symbolic Logic, 49(1), 192–203.
Horsten, L. (1996). Reflecting in epistemic arithemtic. The Journal of Symbolic Logic, 61, 788–801.
Horsten, L. (1997). Provability in principle and controversial constructivistic principles. Journal of Philosophical Logic, 26(6), 635–660.
Horsten, L. (1998). In defence of epistemic arithmetic. Synthese, 116, 1–25.
Koellner, P. (2016). Gödel’s disjunction. In L. Horsten & P. Welch (Eds.), Gödel’s disjunction: the scope and limits of mathematical knowledge. Oxford University Press.
Kripke, S. A. (1975). Outline of a theory of truth. Journal of Philosophy, 72(19), 690–716.
Leitgeb, H. (2009). On formal and informal provability. In New Waves in Philosophy of Mathematics, (pp. 263–299). Palgrave Macmillan.
Pawlowski, P., & Urbaniak, R. (2017). Many-valued logic of informal provability: a non-deterministic strategy [accepted and forthcoming]. The Review of Symbolic Logic.
Rav, Y. (1999). Why do we prove theorems? Philosophia Mathematica, 7(1), 5–41.
Rav, Y. (2007). A critique of a formalist-mechanist version of the justification of arguments in mathematicians’ proof practices. Philosophia Mathematica, 15(3), 291–320.
Reinhardt, W. N. (1986). Epistemic theories and the interpretation of Gödel’s incompleteness theorems. Journal of Philosophical Logic, 15(4), 427–74.
Shapiro, S. (1985). Epistemic and intuitionistic arithemtic. In Intensional mathematics: North Holland.
Solovay, R. (1976). Provability interpretations of modal logic. Israel Journal of Mathematics, 25.
Tanswell, F. (2015). A problem with the dependence of informal proofs on formal proofs. Philosophia Mathematica, 23(3), 295–310.
Acknowledgements
I Would like to thank to Rafal Urbaniak for his time and comments on the previous versions of this paper.
Funding
This work has been supported by FWO [Research Fuoundation Flanders].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Pawlowski, P. Non-deterministic Logic of Informal Provability has no Finite Characterization. J of Log Lang and Inf 30, 805–817 (2021). https://doi.org/10.1007/s10849-021-09344-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10849-021-09344-9