Skip to main content
SpringerLink
Log in

Spatially Varying Mixtures Incorporating Line Processes for Image Segmentation

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

Abstract

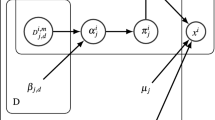
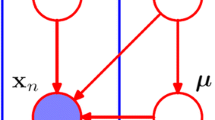
Spatially varying mixture models are characterized by the dependence of their mixing proportions on location (contextual mixing proportions) and they have been widely used in image segmentation. In this work, Gauss-Markov random field (MRF) priors are employed along with spatially varying mixture models to ensure the preservation of region boundaries in image segmentation. To preserve region boundaries, two distinct models for a line process involved in the MRF prior are proposed. The first model considers edge preservation by imposing a Bernoulli prior on the normally distributed local differences of the contextual mixing proportions. It is a discrete line process model whose parameters are computed by variational inference. The second model imposes Gamma prior on the Student’s-t distributed local differences of the contextual mixing proportions. It is a continuous line process whose parameters are also automatically estimated by the Expectation-Maximization (EM) algorithm. The proposed models are numerically evaluated and two important issues in image segmentation by mixture models are also investigated and discussed: the constraints to be imposed on the contextual mixing proportions to be probability vectors and the MRF optimization strategy in the frameworks of the standard and variational EM algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Xu, R., Wunsch II, D.: Survey of clustering algorithms. IEEE Trans. Neural Netw. 16(3), 645–678 (2005)

    Article  Google Scholar 

  2. Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, Berlin (2006)

    Book  MATH  Google Scholar 

  3. Dempster, P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 39(1), 1–38 (1977)

    MATH  MathSciNet  Google Scholar 

  4. Carson, C., Belongie, S., Greenspan, H., Malik, J.: Blobworld: image segmentation using expectation-maximization and its application to image querying. IEEE Trans. Pattern Anal. Mach. Intell. 24(8), 1026–1038 (2002)

    Article  Google Scholar 

  5. Geman, S., Geman, D.: Stochastic relaxation, Gibbs distribution and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 24(6), 721–741 (1984)

    Article  Google Scholar 

  6. Besag, J.: On the statistical analysis of dirty pictures. J. R. Stat. Soc. 48(3), 259–302 (1986)

    MATH  MathSciNet  Google Scholar 

  7. Besag, J.: Statistical analysis of non-lattice data. Statistician 24, 179–195 (1975)

    Article  Google Scholar 

  8. Molina, R., Mateos, J., Katsaggelos, A.K., Vega, M.: Bayesian multichannel image restoration using compound Gauss-Markov random fields. IEEE Trans. Image Process. 12, 1642–1654 (2003)

    Article  Google Scholar 

  9. Kanemura, A., Maeda, S., Ishii, S.: Edge-preserving Bayesian image superresolution based on compound Markov random fields. In: Proceedings of the 17th International conference on Artificial Neural Networks, Porto, Portugal (2007)

  10. Winkler, G.: Image Analysis, Random Fields and Markov Chain Monte Carlo Methods. Springer, Berlin (2006)

    Google Scholar 

  11. Celeux, G., Forbes, F., Peyrard, N.: EM procedures using mean field-like approximations for Markov model-based image segmentation. Pattern Recognit. 36, 131–144 (2003)

    Article  MATH  Google Scholar 

  12. Kohli, P., Torr, P.H.S.: Dynamic graph cuts for efficient inference in Markov random fields. IEEE Trans. Pattern Anal. Mach. Intell. 29(12), 2079–2088 (2007)

    Article  Google Scholar 

  13. Grady, L.: Random walks for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 28(11), 1768–1783 (2006)

    Article  Google Scholar 

  14. Shi, J., Malik, J.: Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 22(8), 888–905 (2000)

    Article  Google Scholar 

  15. Zabih, R., Kolmogorov, V.: Spatially coherent clustering using graph cuts. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’04), vol. 2, pp. 437–444 (2004)

  16. Sanjay-Gopal, S., Hebert, T.: Bayesian pixel classification using spatially variant finite mixtures and the generalized EM algorithm. IEEE Trans. Image Process. 7(7), 1014–1028 (1998)

    Article  Google Scholar 

  17. Blekas, K., Likas, A., Galatsanos, N., Lagaris, I.: A spatially constrained mixture model for image segmentation. IEEE Trans. Neural Netw. 16(2), 494–498 (2005)

    Article  Google Scholar 

  18. Nikou, C., Galatsanos, N., Likas, A.: A class-adaptive spatially variant mixture model for image segmentation. IEEE Trans. Image Process. 16(4), 1121–1130 (2007)

    Article  MathSciNet  Google Scholar 

  19. Marroquin, J., Arce, E., Botello, S.: Hidden Markov measure field models for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 25(11), 1380–1387 (2003)

    Article  Google Scholar 

  20. Rivera, M., Ocegueda, O., Marroquin, J.L.: Entropy-controlled quadratic Markov measure field models for efficient image segmentation. IEEE Trans. Image Process. 16(12), 3047–3057 (2007)

    Article  MathSciNet  Google Scholar 

  21. Rivera, M., Dalmau, O., Tago, J.: Image segmentation by convex quadratic programming. In: 19th International Conference on Pattern Recognition, Tampa, FL (2008)

  22. Diplaros, A., Vlassis, N., Gevers, T.: A spatially constrained generative model and an EM algorithm for image segmentation. IEEE Trans. Neural Netw. 18(3), 798–808 (2007)

    Article  Google Scholar 

  23. Blake, A., Zisserman, A.: Visual Reconstruction. MIT Press, Cambridge (1987)

    Google Scholar 

  24. Black, M.J., Rangarajan, A.: On the unification of line processes, outliers rejection and robust statistics in early vision. Int. J. Comput. Vis. 19(1), 57–91 (1996)

    Article  Google Scholar 

  25. Peel, D., McLachlan, G.J.: Robust mixture modeling using the t-distribution. Stat. Comput. 10, 339–348 (2000)

    Article  Google Scholar 

  26. Sfikas, G., Nikou, C., Galatsanos, N.: Edge preserving spatially varying mixtures for image segmentation. In: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA (2008)

  27. Sfikas, G., Nikou, C., Galatsanos, N., Heinrich, C.: MR brain tissue classification using an edge-preserving spatially variant Bayesian mixture model. In: Proceedings of the 11th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI’08), vol. 1, pp. 43–50, New York, USA (2008)

  28. McLachlan, G.: Finite Mixture Models. Wiley-Interscience, New York (2000)

    Book  MATH  Google Scholar 

  29. Xia, G.S., He, C., Sun, H.: A rapid and automatic MRF-based clustering method for SAR images. IEEE Geosci. Remote Sens. Lett. 4(4), 596–600 (2007)

    Article  Google Scholar 

  30. Birkhoff, G., MacLane, S.: A Survey of Modern Algebra. McMillan, New York (1953)

    MATH  Google Scholar 

  31. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, Berlin (1999)

    Book  MATH  Google Scholar 

  32. Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Kolmogorov, V., Agarwala, A., Tappen, M., Rother, C.: A comparative study of energy minimization methods for Markov random fields. In: Proceedings of the European Conference on Computer Vision (ECCV’06), Graz, Austria (2006)

  33. Zhang, Y., Brady, M., Smith, S.: Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 20(1), 45–57 (2001)

    Article  Google Scholar 

  34. Unnikrishnan, R., Pantofaru, C., Hebert, M.: Toward objective evaluation of image segmentation algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 29(6), 929–944 (2007)

    Article  Google Scholar 

  35. Comaniciu, D., Meer, P.: Mean shift: a robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 24(5), 603–619 (2002)

    Article  Google Scholar 

  36. Martin, D., Fowlkes, C., Tal, D., Malik, J.: A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In: Proceedings of the 8th International Conference on Computer Vision (ICCV ’01), vol. 2, pp. 416–423, July 2001

  37. Freixenet, J., Munoz, X., Raba, D., Marti, J., Cuff, X.: Yet another survey on image segmentation: region and boundary information integration. In: Lecture Notes in Computer Science. Proceedings of the European Conference on Computer Vision (ECCV’02), pp. 408–422 (2002)

  38. Bishop, C., Svensen, M.: Robust Bayesian mixture modeling. In: Proceedings of the 12th European Symposium on Artificial Neural Networks (ESANN’04), Bruges, Belgium (2004)

  39. Sfikas, G., Nikou, C., Galatsanos, N.: Robust image segmentation with mixtures of Student’s t-distributions. In: Proceedings of the 14th International Conference on Image Processing (ICIP’07), San Antonio, TX, USA (2007)

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Ioannina, 45110, Ioannina, Greece

    Giorgos Sfikas & Christophoros Nikou

  2. Department of Electrical and Computer Engineering, University of Patras, 26500, Rio, Greece

    Nikolaos Galatsanos

  3. Laboratoire des Sciences de l’Image de l’Informatique et de la Télédétection / LSIIT, UMR CNRS-ULP 7005, University of Strasbourg, BP 67412, Illkirch cedex, France

    Giorgos Sfikas & Christian Heinrich

Authors
  1. Giorgos Sfikas
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christophoros Nikou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nikolaos Galatsanos
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Christian Heinrich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christophoros Nikou.

Additional information

Giorgos Sfikas was supported by a grant from Région Alsace (France).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Sfikas, G., Nikou, C., Galatsanos, N. et al. Spatially Varying Mixtures Incorporating Line Processes for Image Segmentation. J Math Imaging Vis 36, 91–110 (2010). https://doi.org/10.1007/s10851-009-0174-x

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-009-0174-x

Keywords

Search

Navigation