Abstract
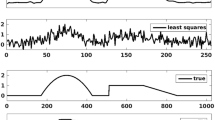
We formulate various variational problems in which the smoothness of functions is measured using Besov space semi-norms. Equivalent Besov space semi-norms can be defined in terms of moduli of smoothness or sequence norms of coefficients in appropriate wavelet expansions. Wavelet-based semi-norms have been used before in variational problems, but existing algorithms do not preserve edges, and many result in blocky artifacts. Here, we devise algorithms using moduli of smoothness for the \(B^1_\infty (L_1(I))\) Besov space semi-norm. We choose that particular space because it is closely related both to the space of functions of bounded variation, \({\text {BV}}(I)\), that is used in Rudin–Osher–Fatemi image smoothing, and to the \(B^1_1(L_1(I))\) Besov space, which is associated with wavelet shrinkage algorithms. It contains all functions in \({\text {BV}}(I)\), which include functions with discontinuities along smooth curves, as well as “fractal-like” rough regions; examples are given in an appendix. Furthermore, it prefers affine regions to staircases, potentially making it a desirable regularizer for recovering piecewise affine data. While our motivations and computational examples come from image processing, we make no claim that our methods “beat” the best current algorithms. The novelty in this work is a new algorithm that incorporates a translation-invariant Besov regularizer that does not depend on wavelets, thus improving on earlier results. Furthermore, the algorithm naturally exposes a range of scales that depends on the image data, noise level, and the smoothing parameter. We also analyze the norms of smooth, textured, and random Gaussian noise data in \(B^1_\infty (L_1(I))\), \(B^1_1(L_1(I))\), \({\text {BV}}(I)\) and \(L^2(I)\) and their dual spaces. Numerical results demonstrate properties of solutions obtained from this moduli of smoothness-based regularizer.






Similar content being viewed by others
Notes
The crucial point is to see that we can take the local polynomial approximation in formula (4.18) of DeVore and Popov [12] to be identically zero on dyadic subsquares that are not entirely contained in the support of a single \(\phi _{j,k}\)—the self-similarity of f means that the local error with approximation zero is a fixed multiple of the error with the best linear polynomial approximation on each subsquare, and hence is near optimal with a constant that doesn’t depend on the scale.
References
Anzellotti, G., Giaquinta, M.: BV functions and traces. Rend. Sem. Mat. Univ. Padova 60, 1–21 (1979) (1978). http://www.numdam.org/item?id=RSMUP_1978__60__1_0
Aujol, J.F., Chambolle, A.: Dual norms and image decomposition models. Int. J. Comput. Vis. 63(1), 85–104 (2005). https://doi.org/10.1007/s11263-005-4948-3
Aujol, J.F., Aubert, G., Blanc-Fraud, L., Chambolle, A.: Image decomposition into a bounded variation component and an oscillating component. J. Math. Imaging Vis. 22(1), 71–88 (2005). https://doi.org/10.1007/s10851-005-4783-8
Bredies, K., Kunisch, K., Pock, T.: Total generalized variation. SIAM J. Imaging Sci. 3(3), 492–526 (2010). https://doi.org/10.1137/090769521
Chambolle, A.: Total variation minimization and a class of binary MRF models. In: Rangarajan, A., Vemuri, B., Yuille, A.L. (eds.) Energy Minimization Methods in Computer Vision and Pattern Recognition: 5th International Workshop, EMMCVPR 2005, St. Augustine, FL, USA, November 9–11, 2005: Proceedings, LNCS 3757. Springer, pp. 136–152 (2005)
Chambolle, A., Pock, T.: A first-order primal–dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011). https://doi.org/10.1007/s10851-010-0251-1
Chambolle, A., DeVore, R.A., Lee, N.Y., Lucier, B.J.: Nonlinear wavelet image processing: variational problems, compression, and noise removal through wavelet shrinkage. IEEE Trans. Image Process. 7(3), 319–335 (1998). https://doi.org/10.1109/83.661182
Chambolle, A., Levine, S.E., Lucier, B.J.: An upwind finite-difference method for total variation-based image smoothing. SIAM J. Imaging Sci. 4(1), 277–299 (2011). https://doi.org/10.1137/090752754
Cramér, H.: Mathematical Methods of Statistics. Princeton Mathematical Series, vol. 9. Princeton University Press, Princeton (1946)
DeVore, R.A., Lorentz, G.G.: Constructive Approximation, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 303. Springer, Berlin (1993)
DeVore, R.A., Lucier, B.J.: Fast wavelet techniques for near-optimal image processing. In: Military Communications Conference, 1992. MILCOM’92, Conference Record. Communications—Fusing Command, Control and Intelligence, vol. 3. IEEE, pp. 1129–1135 (1992). https://doi.org/10.1109/MILCOM.1992.244110
DeVore, R.A., Popov, V.A.: Interpolation of Besov spaces. Trans. Am. Math. Soc. 305(1), 397–414 (1988)
DeVore, R.A., Jawerth, B., Lucier, B.J.: Image compression through wavelet transform coding. IEEE Trans. Inf. Theory 38(2, part 2), 719–746 (1992). https://doi.org/10.1109/18.119733
Ditzian, Z., Ivanov, K.G.: Minimal number of significant directional moduli of smoothness. Anal. Math. 19(1), 13–27 (1993). https://doi.org/10.1007/BF01904036
Donoho, D.L., Johnstone, I.M.: Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 90(432), 1200–1224 (1995). http://links.jstor.org/sici?sici=0162-1459(199512)90:432<1200:ATUSVW>2.0.CO;2-K&origin=MSN
Haddad, A., Meyer, Y.: Variational methods in image processing. In: Perspectives in Nonlinear Partial Differential Equations, Contemporary Mathematics, vol. 446, American Mathematical Society, Providence, RI, pp. 273–295, (2007). https://doi.org/10.1090/conm/446/08636
Papafitsoros, K., Schönlieb, C.: A combined first and second order variational approach for image reconstruction. J. Math. Imaging Vis. 48(2), 308–338 (2014). https://doi.org/10.1007/s10851-013-0445-4
Ridders, C.: A new algorithm for computing a single root of a real continuous function. IEEE Trans. Circuits Syst. 26(11), 979–980 (1979). https://doi.org/10.1109/TCS.1979.1084580
Rockafellar, R.T.: Convex Analysis. Princeton Landmarks in Mathematics. Princeton University Press, Princeton (1997). (reprint of the 1970 original, Princeton Paperbacks)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 60(14), 259–268 (1992). https://doi.org/10.1016/0167-2789(92)90242-F
Sauer, K., Bouman, C.: Bayesian estimation of transmission tomograms using segmentation based optimization. IEEE Trans. Nuclear Sci. 39(4), 1144–1152 (1992). https://doi.org/10.1109/23.159774
Schneider, C.: Trace operators in Besov and Triebel–Lizorkin spaces. Z. Anal. Anwend. 29(3), 275–302 (2010). https://doi.org/10.4171/ZAA/1409
Wang, Z.: SSIM index with automatic downsampling, version 1.0. (2009). https://www.mathworks.com/matlabcentral/answers/uploaded_files/29995/ssim.m. Accessed 27 July 2017
Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13(4), 600–612 (2004). https://doi.org/10.1109/TIP.2003.819861
Author information
Authors and Affiliations
Corresponding author
Additional information
BJL was supported in part by the Office of Naval Research, Contract N00014-91-J-1076, the Institute for Mathematics and its Applications, Minneapolis, USA, and the Simons Foundation (Awards #209418 and #229816). SEL and JDC were supported in part by NSF-DMS 1320829. AC acknowledges the support of the Isaac Newton Institute, Cambridge, and of a grant of the Simons Foundation.
Appendix
Appendix
Here we describe a family of self-similar functions with fractal-like properties that illustrate some of the differences between membership in the Besov space \(B^1_\infty (L_1(I))\) and the space of functions of bounded variation \({\text {BV}}(I)\).
We begin with the function \(\varPhi \) that is continuous on \(\mathbb R^2\), zero outside of I, with \(\varPhi ((\frac{1}{2},\frac{1}{2}))=1\), and a linear polynomial on the triangles in I delineated by the boundary of I, the line \(x_2=x_1\), and the line \(x_1+x_2=1\). The graph of \(\varPhi \) is a pyramid with base I and height 1.
We define \(\phi (x)=\frac{1}{4}\varPhi (2x)\), so \(\phi \) is a scaled dyadic dilate of \(\varPhi \) with support \([0,1/2]^2\).
We construct the sequence of functions \(f_0(x)=\phi (x)\) and
We see that \(f_k\) consists of \(f_{k-1}\) plus \(3^k\) dyadically dilated translates \(\phi _{j,k}(x)=\phi (2^kx-j)\) for some multi-indices \(j=(j_1,j_2)\) with coefficients \((2/3)^k\). The supports of all the \(\phi _{j,k}\) are essentially disjoint.
Finally, we let \(f=\lim _{k\rightarrow \infty }f_k\). We can write
Thus, f is an infinite sum of scaled, dilated, and translated versions of the single pyramid \(\varPhi \); Fig. 7 illustrates the graph of f.
Graph of the function f in (28) that is in \(B^1_\infty (L_1(I))\) but not in \({\text {BV}}(I)\)
The arguments in DeVore and Popov [12]Footnote 1 show that for any \(0<p,q\le \infty \) and \(\alpha < \min (2,1+1/p)\) we have
with the usual changes when p or q are \(\infty \). In our case, we have
where for each k there are \(3^k\) different offsets j.
We note that \(\Vert \phi _{j,k}\Vert _{L_1(I)}=4^{-k}\Vert \phi \Vert _{L_1(I)}\); because there are \(3^k\) terms in the sum for each k,
and we have \(\Vert f\Vert _{B^1_\infty (L_1(I))}\asymp \Vert \phi \Vert _{L_1(I)}<\infty \).
We’ll now see that f is not in \({\text {BV}}(I)\). Denoting the variation of f by V(f), a simple scaling argument shows that \(V(\phi _{j,k})=2^{-k}V(\phi )\). Since the supports of all the \(\phi _{j,k}\) in the definition of f are essentially disjoint, the co-area formula shows that
In other words, there is a constant C such that for all \(h\in \mathbb R^2\),
but there is no constant C such that for all \(h\in \mathbb R^2\),
Note that by replacing 2 / 3 in (27) with any \(0<r<2/3\), the resulting limit f is in both \(B^1_\infty (L_1(I))\) and \({\text {BV}}(I)\) (indeed, it’s in \(B^1_1(L_1(I))\subset {\text {BV}}(I)\)). In this case, we have
so the variation of f tends to \(\infty \) as \(r\rightarrow 2/3\) (as one might expect), while \(\Vert f\Vert _{B^1_\infty (L_1(I))}\) remains bounded.
And if \(r>2/3\), the function f is in neither \({\text {BV}}(I)\) nor \({B^1_\infty (L_1(I))}\).
Thus both \({\text {BV}}(I)\) and \({B^1_\infty (L_1(I))}\) contain fractal-like functions, but their norms in \({B^1_\infty (L_1(I))}\) can be arbitrarily smaller than their norms in \({\text {BV}}(I)\).
Rights and permissions
About this article
Cite this article
Buzzard, G.T., Chambolle, A., Cohen, J.D. et al. Pointwise Besov Space Smoothing of Images. J Math Imaging Vis 61, 1–20 (2019). https://doi.org/10.1007/s10851-018-0821-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-018-0821-1