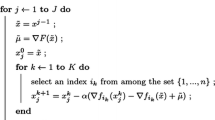Abstract
We propose a new model and a corresponding iterative algorithm for Computed Tomography (CT) when the view angles are uncertain. The uncertainty is described by an additive model discrepancy term which is included in the data fidelity term of a total variation regularized variational model. We approximate the model discrepancy with a Gaussian distribution. Our iterative algorithm alternates between updating the CT reconstruction and parameters of the model discrepancy. By assuming that the uncertainties in the view angles are independent we achieve a covariance matrix structure that we can take advantage of in a stochastic primal dual method to greatly reduce the computational work compared to classical primal dual methods. Using simulations with 2D problems we demonstrate that our method is able to reduce the reconstruction error and improve the visual quality, compared to methods that ignore the uncertainties in the angles.




Similar content being viewed by others
References
Arridge, S.R., Kaipio, J.P., Kolehmainen, V., Schweiger, M., Somersalo, E., Tarvainen, T., Vauhkonen, M.: Approximation errors and model reduction with an application in optical diffusion tomography. Inverse Probl. 22(1), 175–195 (2006)
Basu, S., Bresler, Y.: Uniqueness of tomography with unknown view angles. IEEE Trans. Image Process. 9(6), 1094–1106 (2000)
Benning, M., Burger, M.: Modern regularization methods for inverse problems. Acta Numer. 27, 1–111 (2018)
Brandt, C., Seppänen, A.: Recovery from errors due to domain truncation in magnetic particle imaging: approximation error modeling approach. J. Math. Imaging Vis. 60(8), 1196–1208 (2018)
Buzug, T.M.: Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Springer, Berlin (2008)
Calvetti, D., Dunlop, M., Somersalo, E., Stuart, A.: Iterative updating of model error for Bayesian inversion. Inverse Probl. 34(2), 025008 (2018)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Dongarra, J., Moler, C., Bunch, J., Stewart, G.: LINPACK Users’ Guide. SIAM, Philadephia (1979)
Ehrhardt, M.J., Markiewicz, P.J., Schönlieb, C.B.: Faster PET reconstruction with non-smooth priors by randomization and preconditioning. Phys. Med. Biol. 64(22), 225019 (2019)
Fang, Y., Murugappan, S., Ramani, K.: Estimating view parameters from random projections for tomography using spherical MDS. BMC Med. Imaging 10(1), 12 (2010)
Hansen, T.M., Cordua, K.S., Holm Jacobsen, B., Mosegaard, K.: Accounting for imperfect forward modeling in geophysical inverse problems—exemplified for crosshole tomography. Geophysics 79(3), H1–H21 (2014)
Kaipio, J., Somersalo, E.: Statistical and Computational Inverse Problems. Springer, New York (2005)
Kaipio, J., Somersalo, E.: Statistical inverse problems: discretization, model reduction and inverse crimes. J. Comput. Appl. Math. 198(2), 493–504 (2007)
Kennedy, M.C., O’Hagan, A.: Bayesian calibration of computer models. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 63(3), 425–464 (2001)
Kolehmainen, V., Tarvainen, T., Arridge, S.R., Kaipio, J.P.: Marginalization of uninteresting distributed parameters in inverse problems—application to diffuse optical tomography. Int. J. Uncertain. Quantif. 1(1), 1–17 (2011)
Korolev, Y., Lellmann, J.: Image reconstruction with imperfect forward models and applications in deblurring. SIAM J. Imaging Sci. 11(1), 197–218 (2018)
Natterer, F.: The Mathematics of Computerized Tomography. Wiley, Chicago (1986)
Niebler, S., Schömer, E., Tjaden, H., Schwanecke, U., Schulze, R.: Projection-based improvement of 3D reconstructions from motion-impaired dental cone beam CT data. Med. Phys. 46(10), 4470–4480 (2019)
Nissinen, A., Heikkinen, L.M., Kaipio, J.P.: The Bayesian approximation error approach for electrical impedance tomography—experimental results. Meas. Sci. Technol. 19(1), 015501 (2007)
Nissinen, A., Kolehmainen, V., Kaipio, J.P.: Reconstruction of domain boundary and conductivity in electrical impedance tomography using the approximation error approach. Int. J. Uncertain. Quantif. 1(3), 203–222 (2011)
Madsen, R.B., Hansen, T.M.: Estimation and accounting for the modeling error in probabilistic linearized amplitude variation with offset inversion. Geophysics 83(2), N15–N30 (2018)
Mallick, S.P., Agarwal, S., Kriegman, D.J., Belongie, S.J., Carragher, B., Potter, C.S.: Structure and view estimation for tomographic reconstruction: a Bayesian approach. In: Fitzgibbon, A., Taylor, C.J., Lecun, Y. (eds.) 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), 2(1):2253–2260 (2006)
Peng, C.B., Rodi, W.L., Toksöz, M.N.: A Tikhonov regularization method for image reconstruction. In: Wei, Y., Gu, B. (eds.) Acoustical Imaging, vol. 20, pp. 153–164. Springer, Berlin (1993)
Pulkkinen, A., Kolehmainen, V., Kaipio, J.P., Cox, B.T., Arridge, S.R., Tarvainen, T.: Approximate marginalization of unknown scattering in quantitative photoacoustic tomography. Inverse Probl. Imaging 8(3), 811–829 (2014)
Riis, N.A.B., Dong, Y.: A new iterative method for CT reconstruction with uncertain view angles. In: Lellmann, J., Burger, M., Modersitzki, J. (eds.) Scale Space and Variational Methods in Computer Vision. SSVM 2019. Lecture Notes in Computer Science, vol. 11603, pp. 156–167. Springer, Berlin (2019)
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60(1–4), 259–268 (1992)
Sidky, E.Y., Pan, X.: Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 53(17), 4777–4807 (2008)
Tick, J., Pulkkinen, A., Tarvainen, T.: Modelling of errors due to speed of sound variations in photoacoustic tomography using a Bayesian framework. Biomed. Phys. Eng. Express 6(1), 015003 (2019)
Tikhonov, A.N.: Solution of incorrectly formulated problems and the regularization method. Soviet Math. Dokl. 4:1035–1038 (1963); English translation of Dokl. Akad. Nauk. SSSR 151:501–504 (1963)
van Aarle, W., Palenstijn, W.J., Cant, J., Janssens, E., Bleichrodt, F., Dabravolski, A., Sijbers, J.: Fast and flexible X-ray tomography using the ASTRA toolbox. Opt. Express 24(22), 25129–25147 (2016)
Acknowledgements
We thank Aku Seppänen for a helpful discussion regarding the block formulation of our variational method. We also thank Matthias Ehrhardt for a discussion on the implementation details of SPDHG for this problem. Finally, we thank the referees for comments and suggestions that helped to improve the presentation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by a Villum Investigator Grant (No. 25893) from The Villum Foundation and by the National Natural Science Foundation of China via Grant 11701388.
Rights and permissions
About this article
Cite this article
Riis, N.A.B., Dong, Y. & Hansen, P.C. Computed Tomography Reconstruction with Uncertain View Angles by Iteratively Updated Model Discrepancy. J Math Imaging Vis 63, 133–143 (2021). https://doi.org/10.1007/s10851-020-00972-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-020-00972-7