Skip to main content
Springer Nature Link
Log in

Boundary Ghosts for Discrete Tomography

  • Published:
Journal of Mathematical Imaging and Vision Aims and scope Submit manuscript

Abstract

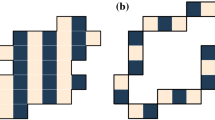
Discrete tomography reconstructs an image of an object on a grid from its discrete projections along relatively few directions. When the resulting system of linear equations is under-determined, the reconstructed image is not unique. Ghosts are arrays of signed pixels that have zero sum projections along these directions; they define the image pixel locations that have non-unique solutions. In general, the discrete projection directions are chosen to define a ghost that has minimal impact on the reconstructed image. Here we construct binary boundary ghosts, which only affect a thin string of pixels distant from the object centre. This means that a large portion of the object around its centre can be uniquely reconstructed. We construct these boundary ghosts from maximal primitive ghosts, configurations of \(2^N\) connected binary (\(\pm 1\)) points over N directions. Maximal ghosts obfuscate image reconstruction and find application in secure storage of digital data.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Alpers, A., Larman, D.G.: The smallest sets of points not determined by their x-rays. Bull. Lond. Math. Soc. 47(1), 171–176 (2015)

    Article  MathSciNet  Google Scholar 

  2. Alpers, A., Tijdeman, R.: The two-dimensional Prouhet-Tarry-Escott problem. J. Number Theory 123, 403–412 (2007)

    Article  MathSciNet  Google Scholar 

  3. Autrusseau, F.: Modélisation psychovisuelle pour le tatouage des images. Ph.D. thesis (2002)

  4. Autrusseau, F., Guedon, J.V., Bizais, Y.: Mojette cryptomarking scheme for medical images. In: Medical Imaging 2003: Image Processing, vol. 5032, pp. 958–965. International Society for Optics and Photonics (2003)

  5. Brunetti, S., Dulio, P., Hajdu, L., Peri, C.: Ghosts in discrete tomography. J. Math. Imag. Vis. 53, 210–224 (2015)

    Article  MathSciNet  Google Scholar 

  6. Cahill, N.D., D Errico, J.R., Spence, J.P.: Complex factorizations of the Fibonacci and Lucas numbers. Fibonacci Quarter. 41(1), 13–19 (2003)

    MathSciNet  MATH  Google Scholar 

  7. Ceko, M., Pagani, S., Tijdeman, R.: Algorithms for linear time reconstruction by discrete tomography II. Discrete Appl. Math. (under review)

  8. Chandra, S.S., Svalbe, I.D., Guédon, J., Kingston, A.M., Normand, N.: Recovering missing slices of the discrete Fourier transform using ghosts. IEEE Trans. Image Process. 21, 4431–4441 (2012)

    Article  MathSciNet  Google Scholar 

  9. Dulio, P., Frosini, A., Pagani, S.M.: A geometrical characterization of regions of uniqueness and applications to discrete tomography. Inverse Probl. 31(12), 125011 (2015)

    Article  MathSciNet  Google Scholar 

  10. Gardner, R., Gritzmann, P.: Discrete tomography: determination of finite sets by X-rays. Trans. Am. Math. Soc. 349, 2271–2295 (1997)

    Article  MathSciNet  Google Scholar 

  11. Golomb, S.W.: Replicating figures in the plane. Math Gazette 48, 403–412 (1964)

    Article  Google Scholar 

  12. Guédon, J.: The Mojette Transform: Theory and Applications. Wiley, Hoboken (2009)

    Google Scholar 

  13. Guédon, J.P., Parrein, B., Normand, N.: Internet distributed image information system. Integr. Comput. Aided Eng. 8(3), 205–214 (2001)

    Article  Google Scholar 

  14. Hajdu, L., Tijdeman, R.: Algebraic aspects of discrete tomography. J. Reine Angew. Math. 534, 119–128 (2001)

    MathSciNet  MATH  Google Scholar 

  15. Katz, M.: Questions of uniqueness and resolution in reconstruction from projections. In: Lecture Notes in Biomathematics, vol. 26. Springer-Verlag, Berlin, Heidelberg (1978)

  16. Normand, N., Kingston, A., Évenou, P.: A geometry driven reconstruction algorithm for the Mojette transform. In: International Conference on Discrete Geometry for Computer Imagery, pp. 122–133. Springer (2006)

  17. Pagani, S., Tijdeman, R.: Algorithms for linear time reconstruction by discrete tomography. Discrete Appl. Math. 271, 152–170 (2019)

    Article  MathSciNet  Google Scholar 

  18. Pertin, D.: Mojette erasure code for distributed storage (Ph.D Thesis). University of Nantes (2016)

  19. Svalbe, I., Ceko, M.: Maximal N-ghosts and minimal information recovery from N projected views of an array. In: International Conference on Discrete Geometry for Computer Imagery, pp. 135–146. Springer (2017)

  20. Svalbe, I., Nazareth, N., Normand, N., Chandra, S.: On constructing minimal ghosts. In: Digital Image Computing: Techniques and Applications (DICTA), pp. 276–281. IEEE (2010)

  21. Van Aert, S., Batenburg, K.J., Rossell, M.D., Erni, R., Van Tendeloo, G.: Three-dimensional atomic imaging of crystalline nanoparticles. Nature 470, 374 (2011)

    Article  Google Scholar 

  22. Varga, L., Balázs, P., Nagy, A.: Projection selection dependency in binary tomography. Acta Cybernetica 20, 167–187 (2011)

    Article  Google Scholar 

Download references

Acknowledgements

The School of Physics and Astronomy at Monash University, Australia, has provided funds for this work. M.C. has the support of the Australian government’s Research Training Program (RTP) and the J. L. William scholarship from the School of Physics and Astronomy at Monash University. The authors thank the referees for their critical remarks which led to improvements in the paper.

Author information

Authors and Affiliations

  1. School of Physics and Astronomy, Monash University, Melbourne, Australia

    Matthew Ceko, Timothy Petersen & Imants Svalbe

  2. Monash Centre for Electron Microscopy, Monash University, Melbourne, Australia

    Timothy Petersen

  3. Mathematical Institute, Leiden University, Leiden, Netherlands

    Rob Tijdeman

Authors
  1. Matthew Ceko
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Timothy Petersen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Imants Svalbe
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Rob Tijdeman
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Matthew Ceko.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ceko, M., Petersen, T., Svalbe, I. et al. Boundary Ghosts for Discrete Tomography. J Math Imaging Vis 63, 428–440 (2021). https://doi.org/10.1007/s10851-020-01010-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10851-020-01010-2

Keywords