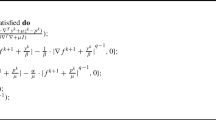Abstract
Our aim is to explain and characterize the behavior of adaptive total variation (TV) regularization. TV has been widely used as an edge-preserving regularizer. However, objects are often over-regularized by TV, becoming blob-like convex structures of low curvature. This phenomenon was explained mathematically in the analysis of Andreau et al. They have shown that a TV regularizer can spatially preserve perfectly sets which are nonlinear eigenfunctions of the form \(\lambda u \in \partial J_{TV}(u)\), where \(\partial J_{TV}(u)\) is the TV subdifferential. For TV, these shapes are indeed convex sets of low curvature. A compelling approach to better preserve structures is to use adaptive anisotropic functionals, which adapt the regularization in an image-driven manner, with strong regularization along edges and low across them. This follows the seminal work of Weickert on anisotropic diffusion. Adaptive anisotropic TV (A\(^2\)TV) was successfully used in several studies in the past decade. However, there is little analysis of the type of structures which can be well preserved. In this study, we address this question by a joint methodology of mathematical derivations and experiments. We rely on a recently developed theory of Burger et al on nonlinear spectral analysis of one-homogeneous functionals. We have that eigenfunction sets, admitting \(\lambda u \in \partial J_{A^2TV}(u)\), are perfectly preserved under A\(^2\)TV flow or minimization with \(L^2\) square fidelity. We thus investigate these eigenfunctions theoretically and numerically. We prove non-convex sets can be eigenfunctions in certain conditions and provide numerical results which characterize well the relations between the degree of local anisotropy of the functional and the admitted maximal curvature. A nonlinear spectral representation is formulated, where shapes are well preserved and can be manipulated effectively. Finally, examples of possible applications related to shape manipulation and guided regularization of medical and depth data are shown.













Similar content being viewed by others
References
Alter, F., Caselles, V., Chambolle, A.: A characterization of convex calibrable sets in. Math. Ann. 332(2), 329–366 (2005)
Andreu, F., Ballester, C., Caselles, V., Mazón, J.M.: Minimizing total variation flow. Differ. Integral Equ. 14(3), 321–360 (2001)
Aubert, G., Aujol, J.F.: A variational approach to removing multiplicative noise. SIAM J. Appl. Math. 68(4), 925–946 (2008)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)
Bellettini, G., Caselles, V., Novaga, M.: The total variation flow in \(\mathbb{R}^n\). J. Differ. Equ. 184(2), 475–525 (2002)
Bellettini, G., Caselles, V., Novaga, M.: The total variation flow in \(R^N\). J. Differ. Equ. 184(2), 475–525 (2002)
Brezis, H.: Ope| rateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, vol. 5. Elsevier (1973)
Brinkmann, E.M., Burger, M., Rasch, J., Sutour, C.: Bias reduction in variational regularization. J. Math. Imaging Vis. 59(3), 534–566 (2017)
Bungert, L., Burger, M.: Asymptotic profiles of nonlinear homogeneous evolution equations of gradient flow type. J. Evol. Equ. 20, 1061–1092 (2020)
Bungert, L., Burger, M., Chambolle, A., Novaga, M.: Nonlinear spectral decompositions by gradient flows of one-homogeneous functionals. Anal. PDE 14(3), 823–860 (2021)
Burger, M., Gilboa, G., Moeller, M., Eckardt, L., Cremers, D.: Spectral decompositions using one-homogeneous functionals. SIAM J. Imag. Sci. 9(3), 1374–1408 (2016)
Burger, M., Gilboa, G., Osher, S., Xu, J.: Nonlinear inverse scale space methods. Commun. Math. Sci. 4(1), 179–212 (2006)
Burger, M., Osher, S.: A guide to the tv zoo. In: Level Set and PDE Based Reconstruction Methods in Imaging, pp. 1–70. Springer (2013)
Chambolle, A.: An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 20(1), 89–97 (2004)
Chambolle, A., Caselles, V., Cremers, D., Novaga, M., Pock, T.: An introduction to total variation for image analysis. Theor. Found. Numer. Methods Sparse Recovery 9(263–340), 227 (2010)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40(1), 120–145 (2011)
Cohen, I., Gilboa, G.: Introducing the p-laplacian spectra. Signal Process. 167, 107281 (2020)
Deledalle, C.A., Papadakis, N., Salmon, J., Vaiter, S.: Clear: Covariant least-square refitting with applications to image restoration. SIAM J. Imag. Sci. 10(1), 243–284 (2017)
Di Zenzo, S.: A note on the gradient of a multi-image. Comput. Vis. Graph. Image Process. 33(1), 116–125 (1986)
Duan, J., Ward, W.O., Sibbett, L., Pan, Z., Bai, L.: Introducing anisotropic tensor to high order variational model for image restoration. Digital Signal Process. (2017)
Gilboa, G.: A spectral approach to total variation. In: International Conference on Scale Space and Variational Methods in Computer Vision, pp. 36–47. Springer (2013)
Gilboa, G.: A total variation spectral framework for scale and texture analysis. SIAM J. Imag. Sci. 7(4), 1937–1961 (2014)
Gilboa, G.: Semi-inner-products for convex functionals and their use in image decomposition. J. Math. Imag. Vis. 57(1), 26–42 (2017)
Gilboa, G., Moeller, M., Burger, M.: Nonlinear spectral analysis via one-homogeneous functionals: Overview and future prospects. J. Math. Imag. Vis. 56(2), 300–319 (2016). https://doi.org/10.1007/s10851-016-0665-5
Giusti, E.: On the equation of surfaces of prescribed mean curvature. Invent. Math. 46(2), 111–137 (1978)
Grasmair, M., Lenzen, F.: Anisotropic total variation filtering. Appl. Math. Optim. 62(3), 323–339 (2010)
Hong, B.W., Koo, J.K., Soatto, S.: Multi-label segmentation via residual-driven adaptive regularization. arXiv preprint arXiv:1702.08336 (2017)
Kawohl, B., Lachand-Robert, T.: Characterization of cheeger sets for convex subsets of the plane. Pac. J. Math. 225(1), 103–118 (2006)
Krajsek, K., Scharr, H.: Diffusion filtering without parameter tuning: Models and inference tools. In: Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pp. 2536–2543. IEEE (2010)
Li, F., Bao, Z., Liu, R., Zhang, G.: Fast image inpainting and colorization by Chambolle’s dual method. J. Vis. Commun. Image Represent. 22(6), 529–542 (2011)
Min, L., Feng, C.: Compressive sensing reconstruction based on weighted directional total variation. J. Shanghai Jiaotong Univ. (Science) 22(1), 114–120 (2017)
Nossek, R.Z., Gilboa, G.: Flows generating nonlinear eigenfunctions. J. Sci. Comput. 75(2), 859–888 (2018)
Peter, P., Kaufhold, L., Weickert, J.: Turning diffusion-based image colorization into efficient color compression. IEEE Trans. Image Process. 26(2), 860–869 (2017)
Peura, M., Iivarinen, J.: Efficiency of simple shape descriptors. In: Proceedings of the Third International Workshop on Visual Form, vol. 443, p. 451. Citeseer (1997)
Rudin, L., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60, 259–268 (1992)
Schmaltz, C., Peter, P., Mainberger, M., Ebel, F., Weickert, J., Bruhn, A.: Understanding, optimising, and extending data compression with anisotropic diffusion. Int. J. Comput. Vis. 108(3), 222–240 (2014)
Schmidt, M.F., Benning, M., Schönlieb, C.B.: Inverse scale space decomposition. Inverse Prob. 34(4), 045008 (2018)
Steidl, G., Weickert, J., Brox, T., Mrázek, P., Welk, M.: On the equivalence of soft wavelet shrinkage, total variation diffusion, total variation regularization, and sides. SIAM J. Numer. Anal. 42(2), 686–713 (2004)
Suwajanakorn, S., Hernandez, C., Seitz, S.M.: Depth from focus with your mobile phone. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 3497–3506 (2015)
Weickert, J.: Anisotropic Diffusion in Image Processing. B.G Teubner (Stuttgart) (1998)
Welk, M.: Diffusion, pre-smoothing and gradient descent. In: Elmoataz,, A. Fadili, J., Quéau, Y., Rabin, J., Simon, L. (eds.) Scale Space and Variational Methods in Computer Vision, pp. 78–90. Springer, Berlin (2021)
Zach, C., Pock, T., Bischof, H.: A duality based approach for realtime tv-l 1 optical flow. In: Joint Pattern Recognition Symposium, pp. 214–223. Springer (2007)
Zhao, Z., Kumar, A.: An accurate iris segmentation framework under relaxed imaging constraints using total variation model. In: Computer Vision (ICCV), 2015 IEEE International Conference on, pp. 3828–3836. IEEE (2015)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
A\(^2\)TV Curvature Condition
We would like to find the relation of the maximal curvature on the set boundary to the degree of anisotropy (the parameter \(a \in (0,1]\)). Let us first discuss the extreme cases. For \(a=1\), we get isotropic TV; therefore, the bound should be as in Eq. (14). As a decreases, the regularization diminishes and we expect the bound to grow as \(a \rightarrow 0\).
We now turn to examining more closely the dual variable \(\xi ^A\) from the A\(^2\)TV functional weak sense definition Eq. (20). As \(\xi ^A\) is coupled inside \({{\,\mathrm{div}\,}}_A\), we would like to separate the influence of the adapted anisotropic matrix A from the \({{\,\mathrm{div}\,}}\); therefore, we define
In Fig. 14, one can see the differences between the vector fields \(\tilde{\xi ^A}\) and \(\xi ^A\). Note especially the smoother behavior of \(\tilde{\xi ^A}\) near edges.
Comparison between the vector fields \(\xi ^A\) (defined by Eq. (20)) and \(\tilde{\xi ^A}\), Eq. (62), (a=0.5). From left: indicator function of a non-convex set C, color-coded vector field \(\xi ^A\) and the cross-sectional vertical line (in red), cross sections of \(\xi ^A\) and \(\tilde{\xi ^A}\). Whereas \(\xi ^A\) is not smooth near the edge, \(\tilde{\xi ^A}\) is smooth (Color figure online)
Let us compare the TV Definition 2 and the A\(^2\)TV Definition 4. For eigenfunctions, \(\xi \) for TV and \(\tilde{\xi ^A}\) for A\(^2\)TV, should have a constant divergence. We denote both vector fields by \(\xi \). In two dimensions, a vector field has a constant divergence when its components are of the form,
for some differentiable function \(R(\cdot )\). Clearly, we get by construction a constant divergence: \(\text {div}(\xi ) = t_1+ t_2\). For total variation the function \(R(\cdot )\) is identically zero (for a disk of radius r we get \(R(\cdot )=0, t_1=t_2=\frac{1}{r}\)). However, our numerical observations indicate it is a more complex function for A\(^2\)TV. For example, in the case of ellipses, \(\tilde{\xi ^A}\) has a structure similar to a third-degree polynomial (as shown in Fig. 16).
Several numerical experiments were conducted using ellipse shapes (as in Fig. 15) with various eccentricities and A\(^2\)TV regularization with various degrees of anisotropy parameter (a). An ellipse shape is used in order to decouple the convexity and the curvature measures. Moreover, it is simple to estimate numerically its curvature.
For an ellipse, as in Fig. 15, \(R_a\ge R_b\), the maximum curvature, located at \((x,y)=(R_a,0)\), is
Our numerical experiments are based on the schemes detailed in Sect. 5. We compute the vector field \(\tilde{\xi ^A}=(\tilde{\xi ^A_x},\tilde{\xi ^A_y})\), Eq. (62), based on the dual variable \(\xi ^A\) for a given function u (see the definition of A\(^2\)TV, Eq. (20)). Since the vector field has two components (in 2D), we show cross sections of both \(\tilde{\xi ^A_x}\) and \(\tilde{\xi ^A_y}\). The first experiment is done by applying A\(^2\)TV on a single ellipse, \(Ra = 100, Rb = 20\), with various values of the anisotropy parameter a. The resultant \(\tilde{\xi ^A}\) cross sections along the x and y axes are shown in Fig. 16. One can observe that on the minor axis \(\tilde{\xi ^A_y}\) has a linear solution just as in the TV case (due to its low curvature). The major axis, on the other hand, is not a linear function. The curvature on the boundary is maximal and \(\tilde{\xi ^A}\) is not monotone inside the set anymore. For \(a>0.5\), the anisotropy of A\(^2\)TV is not sufficient and one does not obtain an eigenfunction, this can be seen by the clipping of \(\tilde{\xi ^A_x}\) near the value of 1. For \(a\le 0.5\), we get an eigenfunction with \({{\,\mathrm{div}\,}}(\tilde{\xi ^A}) = const\), here \(\tilde{\xi ^A_x}\) resembles a third-degree polynomial.
In Fig. 17, we present results of another numerical experiment. Now, a fixed anisotropic parameter \(a=0.5\) is used and ellipses with various radii ratios (\(r = \frac{R_b}{R_a}\)) are tested. When the eccentricity of the ellipse is low (\(\frac{R_b}{R_a}\) closer to 1) there is a linear profile for both axes. Actually these ellipses are eigenfunction also of TV (ratios of \(r\in (0.6,1]\)). As the eccentricity grows with \(r\in (0.15,0.5]\), we obtain eigenfunctions unique to A\(^2\)TV (with \(a=0.5\)). Finally, we have a very narrow ellipse, \(r = 0.1\), which is not an eigenfunction, where the vector field is clipped.
These experiments show a distinct systematic trend relating the parameter a to the set of ellipse eigenfunctions, which is summarized in Fig. 2. As a becomes smaller, ellipses of higher eccentricity (and curvature) become admissible eigenfunctions.
In order to estimate numerically a curvature condition for ellipses, we performed the following experiment, with the results depicted in Fig. 18. Multiple A\(^2\)TV flows (with different a parameter) were applied to ellipses of different eccentricities (\(R_b/R_a \in (0.2,1]\)).
In Fig. 18, we can see two plots. The left plot shows the eigenfunction test scores (lower is better) based on the following formula,
where u is an ellipse image after applying a A\(^2\)TV flow at \(t = \frac{1}{10\lambda ^A}\) where \(\lambda ^A\) is taken from Eq. (35). The test score, typically in the range \(T(u)\in [0,1]\), was chosen due to its numerical robustness, as oppose to indicators which take into account the entire image, and are biased by numerical errors. We rely on the fundamental property of indicator set eigenfunctions which retain a constant value within the set. The time of the flow chosen for the computation is 10% of the approximated extinction time. The value of \(\epsilon = 0.05 \cdot R_a\) was used (for \(R_a=200\), \(\epsilon = 10\)).
On the left, it can be observed that as the ratio tends to 1 (toward a disk), the shape attains a better eigenfunction score. The bar with the value 0.0017 was chosen so that the ratio 0.6 is the last one to be an eigenfunction for the TV functional (which is the theoretical threshold for TV). From the graph on the left, critical thresholds for a, \(a_{cr}\) values were extracted with the rule of choosing a which gives the same test score T(u) for each ellipse ratio. The right plot shows \(f_{cr}\), which represents a hypothesis that the bound for an A\(^2\)TV eigenfunction in the form of an ellipse has a curvature bound \(\kappa _\mathrm{max}\), where
and the set C represent an ellipse with a major axis \(R_a\) and a minor axis \(R_b\) as shown in Fig. 15. For each ellipse ratio, we took the critical \(a_{cr}\) and applied it as a function of \(f_{cr,Exp}\),
Both images in Fig. 18 present a strong indication that the upper bound dependence on the parameter a is \(\frac{1}{a^3}\). Note that this is the case for ellipses, it is hard to validate whether curvature and convexity/shape structures can be completely decoupled. We summarize this relation in Conjecture 1.
A\(^2\)TV Disk Example
We define the following function,
The shape of f is basically a disk of radius R and height h, within a circular domain \(\varOmega \) of radius \(R_0\). Here, \(c_0=1-R^2/R_0^2\) was chosen so the mean value is \({\bar{f}}=0\). We define the following matrix A as in (25), with \(\partial C: |X|=R\). Eq. (21) can be written as,
In this eigenproblem, the eigenvalue of \(v_1\) is a and of \(v_2\) is 1. Let us assume a certain vector field \(\xi ^A\) and show it is a calibrable set. On the disk boundary \(\partial C\), we require,
The divergence operator is applied on \(A\xi ^A\); therefore, we impose continuity to get,
We compute \(p = {{\,\mathrm{div}\,}}_A \xi ^A = {{\,\mathrm{div}\,}}(A\xi ^A).\) Thus, we obtain,
One can validate the solution admits \(\Vert \xi ^A\Vert _\infty \le 1\):
The eigenvalue can be computed by
Rights and permissions
About this article
Cite this article
Biton, S., Gilboa, G. Adaptive Anisotropic Total Variation: Analysis and Experimental Findings of Nonlinear Spectral Properties. J Math Imaging Vis 64, 916–938 (2022). https://doi.org/10.1007/s10851-022-01097-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-022-01097-9