Abstract
We present a novel certifiable convex method to estimate 3D pose from mixed combinations of 2D–3D point and line correspondences, the Perspective-n-Points-and-Lines problem. We merge the contributions of each point and line into a unified Quadratically Constrained Quadratic Problem and then relax it into a Semidefinite Program through Shor’s relaxation. In this way, we jointly handle mixed configurations of points and lines in a single computational framework. Furthermore, the proposed relaxation allows us to recover a finite number of solutions under ambiguous configurations. In such cases, the 3D pose candidates are found by further enforcing geometric constraints on the solution space and then retrieving such poses from the intersections of multiple quadrics. Experiments provide results in line with the best performing state-of-the-art methods while providing the flexibility of solving for an arbitrary number of points and lines, while the convex formulation provides a framework for a posteriori validation of globally optimal solutions.








Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Abdel-Aziz, Y., Karara, H.: Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry. In: Proceedings of the Symposium on Close-Range Photogrammetry, pp. 1–18. ASP (1971)
Ansar, A., Daniilidis, K.: Linear pose estimation from points or lines. IEEE Trans. Pattern Anal. Mach. Intell. 25(5), 578–589 (2003)
Boyd, S., Boyd, S.P., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Boyd, S., Parikh, N., Chu, E.: Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Now Publishers Inc, Hanover (2011)
Brachmann, E., Krull, A., Michel, F., Gumhold, S., Shotton, J., Rother, C.: Learning 6D object pose estimation using 3D object coordinates. In: European Conference on Computer Vision (ECCV), pp. 536–551. Springer (2014)
Bradski, G.: The OpenCV Library. Dr. Dobb’s Journal of Software Tools (2000)
Briales, J., Gonzalez-Jimenez, J.: Convex global 3D registration with lagrangian duality. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2017)
Briales, J., Kneip, L., Gonzalez-Jimenez, J.: A certifiably globally optimal solution to the non-minimal relative pose problem. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2018)
Carlone, L., Calafiore, G.C., Tommolillo, C., Dellaert, F.: Planar pose graph optimization: duality, optimal solutions, and verification. IEEE Trans. Rob. 32(3), 545–565 (2016)
Chen, H.H.: Pose determination from line-to-plane correspondences: existence condition and closed-form solutions. In: Third International Conference on Computer Vision, pp. 374–378. IEEE (1990)
DeMenthon, D., Davis, L.S.: Exact and approximate solutions of the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 14(11), 1100–1105 (1992)
Dhome, M., Richetin, M., Lapreste, J.T., Rives, G.: Determination of the attitude of 3D objects from a single perspective view. IEEE Trans. Pattern Anal. Mach. Intell. 11(12), 1265–1278 (1989)
Ferraz, L., Binefa, X., Moreno-Noguer, F.: Very fast solution to the PnP problem with algebraic outlier rejection. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2014)
Gao, X.S., Hou, X.R., Tang, J., Cheng, H.F.: Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 25(8), 930–943 (2003)
Hartley, R., Zisserman, A.: Multiple View Geometry in Computer Vision. Cambridge University Press, Cambridge (2003)
Hesch, J.A., Roumeliotis, S.I.: A direct least-squares (DLS) method for PnP. In: 2011 International Conference on Computer Vision, pp. 383–390. IEEE (2011)
Hinterstoisser, S., Lepetit, V., Ilic, S., Holzer, S., Bradski, G., Konolige, K., Navab, N.: Model based training, detection and pose estimation of texture-less 3D objects in heavily cluttered scenes. In: Asian Conference on Computer Vision, pp. 548–562. Springer (2012)
Khoo, Y., Kapoor, A.: Non-iterative rigid 2D/3D point-set registration using semidefinite programming. IEEE Trans. Image Process. 25(7), 2956–2970 (2016)
Kneip, L., Furgale, P.: Opengv: A unified and generalized approach to real-time calibrated geometric vision. In: 2014 IEEE International Conference on Robotics and Automation (ICRA). IEEE (2014)
Kneip, L., Li, H., Seo, Y.: UPnP: An optimal O (n) solution to the absolute pose problem with universal applicability. In: European Conference on Computer Vision (ECCV), pp. 127–142. Springer (2014)
Kuang, Y., Astrom, K.: Pose estimation with unknown focal length using points, directions and lines. In: IEEE International Conference on Computer Vision (ICCV) (2013)
Kukelova, Z., Heller, J., Fitzgibbon, A.: Efficient intersection of three quadrics and applications in computer vision. In: IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (2016)
Lepetit, V., Moreno-Noguer, F., Fua, P.: EPNP: an accurate O (n) solution to the PNP problem. Int. J. Comput. Vis. 81(2), 155 (2009)
Li, S., Xu, C., Xie, M.: A robust O (n) solution to the perspective-n-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 34(7), 1444–1450 (2012)
Lowe, D.G.: Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vision 60(2), 91–110 (2004)
Marchand, E., Uchiyama, H., Spindler, F.: Pose estimation for augmented reality: a hands-on survey. IEEE Trans. Visual Comput. Graphics 22(12), 2633–2651 (2016)
Mirzaei, F.M., Roumeliotis, S.I.: Globally optimal pose estimation from line correspondences. In: 2011 IEEE International Conference on Robotics and Automation, pp. 5581–5588. IEEE (2011)
Nesterov, Y., Wolkowicz, H., Ye, Y.: Semidefinite programming relaxations of nonconvex quadratic optimization. In: Handbook of Semidefinite Programming, pp. 361–419. Springer (2000)
O’Donoghue, B., Chu, E., Parikh, N., Boyd, S.: Conic optimization via operator splitting and homogeneous self-dual embedding. J. Optim. Theory Appl. 169(3), 1042–1068 (2016)
Přibyl, B., Zemčík, P., Čadík, M.: Camera pose estimation from lines using plücker coordinates. In: British Machine Vision Conference (2015)
Přibyl, B., Zemčík, P., Čadík, M.: Absolute pose estimation from line correspondences using direct linear transformation. Comput. Vis. Image Underst. 161, 130–144 (2017)
Ramalingam, S., Bouaziz, S., Sturm, P.: Pose estimation using both points and lines for geo-localization. In: 2011 IEEE International Conference on Robotics and Automation, pp. 4716–4723. IEEE (2011)
Rosen, D.M., Carlone, L., Bandeira, A.S., Leonard, J.J.: Se-sync: a certifiably correct algorithm for synchronization over the special Euclidean group. Int. J. Robot. Res. 38(2–3), 95–125 (2019)
Rosen, D.M., DuHadway, C., Leonard, J.J.: A convex relaxation for approximate global optimization in simultaneous localization and mapping. In: 2015 IEEE International Conference on Robotics and Automation (ICRA), pp. 5822–5829. IEEE (2015)
Saunderson, J., Parrilo, P.A., Willsky, A.S.: Semidefinite descriptions of the convex hull of rotation matrices. SIAM J. Optim. 25(3), 1314–1343 (2015)
Schacke, K.: On the Kronecker product. Master’s thesis, University of Waterloo (2004)
Schweighofer, G., Pinz, A.: Globally optimal O (n) solution to the PNP problem for general camera models. In: British Machine Vision Conference, pp. 1–10 (2008)
Shor, N.Z.: Quadratic optimization problems. Sov. J. Comput. Syst. Sci. 25, 1–11 (1987)
Tron, R., Rosen, D.M., Carlone, L.: On the inclusion of determinant constraints in Lagrangian duality for 3D slam. In: Robotics: Science and Systems (RSS) in the workshop “The Problem of Mobile Sensors” (2015)
Vakhitov, A., Funke, J., Moreno-Noguer, F.: Accurate and linear time pose estimation from points and lines. In: European Conference on Computer Vision (ECCV), pp. 583–599. Springer (2016)
Von Gioi, R.G., Jakubowicz, J., Morel, J.M., Randall, G.: LSD: a fast line segment detector with a false detection control. IEEE Trans. Pattern Anal. Mach. Intell. 32(4), 722–732 (2010)
Xu, C., Zhang, L., Cheng, L., Koch, R.: Pose estimation from line correspondences: a complete analysis and a series of solutions. IEEE Trans. Pattern Anal. Mach. Intell. 39(6), 1209–1222 (2017)
Yang, H., Carlone, L.: A polynomial-time solution for robust registration with extreme outlier rates. arXiv preprint arXiv:1903.08588 (2019)
Ye, Y., Todd, M.J., Mizuno, S.: An O(\(\sqrt{n}\)L)-iteration homogeneous and self-dual linear programming algorithm. Math. Oper. Res. 19(1), 53–67 (1994)
Zhang, L., Xu, C., Lee, K.M., Koch, R.: Robust and efficient pose estimation from line correspondences. In: Asian Conference on Computer Vision, pp. 217–230. Springer (2012)
Zheng, Y., Kuang, Y., Sugimoto, S., Åström, K., Okutomi, M.: Revisiting the PnP problem: a fast, general and optimal solution. In: IEEE International Conference on Computer Vision (ICCV) (2013)
Zhou, L., Yang, Y., Abello, M., Kaess, M.: A robust and efficient algorithm for the PnL problem using algebraic distance to approximate the reprojection distance. In: Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence (2019)
Zhou, L., Ye, J., Kaess, M.: A stable algebraic camera pose estimation for minimal configurations of 2D/3D point and line correspondences. In: Asian Conference on Computer Vision (2018)
Acknowledgements
The authors would like to thank Jacopo Cavazza and all present at the Optimization Methods in Geometric Vision seminar at the 2019 NII Shonan Meetings, for their suggestions and insightful discussions. This work was partially supported by LARSyS - FCT Project UIDB/50009/2020 and the FCT grant PD/BD/114432/2016.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The code implementation and datasets generated during and/or analyzed during the current study are available in its public repository, at https://github.com/SergioRAgostinho/cvxpnpl.
Appendices
Appendix A Useful Vectorization Properties
See [36] for an insightful discussion on the following identities:


where the operator \(\otimes \) represents the Kronecker product.
Appendix B Geometric Constraints
This section contains the detailed derivations showing how to compose the equations systems from §3.
1.1 B.1 Point Correspondences
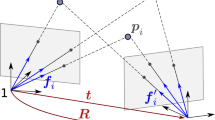
Consider \({\textbf{b}}_i\) as the bearing vector associated with the 3D point \({\textbf{p}}_i\) (refer to Fig. 1). The transformation from the model/object space to the camera is parameterized by the rotation matrix  and the translation vector \({\textbf{t}}\). The collinearity constraint of a point allows us to write,
and the translation vector \({\textbf{t}}\). The collinearity constraint of a point allows us to write,

where \(\lfloor {\textbf{b}} \rfloor _\times \) is the skew symmetric matrix representation of the 3D vector \({\textbf{b}}\)
We can represent Eq. (28) isolating the vectorized representation of  ,
,

as



Matrices  and
and  are \(3\times 9\) and \(3\times 2\), respectively. Each point correspondence contributes 3 equations and upon stacking all n points yields,
are \(3\times 9\) and \(3\times 2\), respectively. Each point correspondence contributes 3 equations and upon stacking all n points yields,

which are \(3n\times 9\) and \(3n\times 3\) sized matrices, respectively. This ultimately results in the homogeneous system of equations

1.2 B.2 Line Correspondences
Consider a 3D line defined by two points, which we represent by the tuple \(({\mathbf{l_p}}_{1j}, {\mathbf{l_p}}_{2j})\). Also consider \({\mathbf{l_n}}_j\), the normal to the plane formed between the 3D line and the origin of the camera. From the coplanarity constraints of the line, we have

and from Eq. (36),




The vector \({\mathbf{c_l}}_{ij} \in {\mathbb {R}}^9\). Stacking the contributions from all m lines yields

which are matrices of size \(2\,m\times 9 \) and \(2\,m\times 3\), respectively. The full system of equations assumes the form

Appendix C The QCQP Reformulation
The reformulation from QCQP problem (7) into its canonical form (8) is required in order to leverage conventional convex solvers. In the next sections, we address this reformulation for each element of the problem. Out of convenience, we resort to the homogenized representation of \({\textbf{r}}\),
as it eases bundling all constant and linear terms with respect to \({\textbf{r}}\), into a quadratic form with respect to \(\tilde{{\textbf{r}}}\).
1.1 C.1 Cost Function
The cost function is defined by
1.2 C.2 Orthogonality of Rows
The constraint associated with the orthogonality ofrows provides 6 linearly independent equations,

where the matrix  represents the identity of size \(3\times 3\). We introduce the unit vector \({\textbf{e}}_i \in \mathbb {R}^3\), whose component i is set to 1 and the remainder to 0, as well as the \(3\times 3\) matrix
represents the identity of size \(3\times 3\). We introduce the unit vector \({\textbf{e}}_i \in \mathbb {R}^3\), whose component i is set to 1 and the remainder to 0, as well as the \(3\times 3\) matrix

which is composed of a unique element 1 at row i and column j, while all the remaining ones are 0. Equipped with these new definitions, we are able to express the constraint in (47) with respect to each individual component. In general, for a given matrix  we have that:
we have that:

Employing the same property we have









Iterating for all indexes, we compose 6 constraints:

1.3 C.3 Orthogonality of Columns
The derivation is very similar to Sec. C.2. This time we start from the following constraint:










Iterating for all indexes composes 6 constraints as:

Appendix D Composing the Linear System of Quadrics
In § 5 we state that, under minimal configurations, the solution space of all admissible solutions is given by the linear decomposition
where K is the rank of matrix  . Consider now the case \(K=4\), which is the highest rank we address in this paper. The three unknowns \(\alpha _1'\), \(\alpha _2'\) and \(\alpha _3'\) will be designated by the letters a, b and c and we will drop the \('\) superscript on the vectors for convenience. We resort to the inverse of the vectorizing operator \({{\,\textrm{vec}\,}}^{-1}\) to reformulate Eq. (71). Defining
. Consider now the case \(K=4\), which is the highest rank we address in this paper. The three unknowns \(\alpha _1'\), \(\alpha _2'\) and \(\alpha _3'\) will be designated by the letters a, b and c and we will drop the \('\) superscript on the vectors for convenience. We resort to the inverse of the vectorizing operator \({{\,\textrm{vec}\,}}^{-1}\) to reformulate Eq. (71). Defining
we can rewrite it as
Once more, for  to be valid, it needs to respect the constraints in Eqs. (7b), (7c) and (7d). In the next sections we will show how to rewrite this combined set of 21 constraints as a linear system
to be valid, it needs to respect the constraints in Eqs. (7b), (7c) and (7d). In the next sections we will show how to rewrite this combined set of 21 constraints as a linear system
where \({{{{\textbf {{\texttt {A}}}}}}}\) is a matrix of size \(21\times 10\).
1.1 D.1 Reformulating the Quadratic System of Equations as a Linear System with Respect to Quadratic Terms
One important aspect of this formulation is recognizing how to convert the quadratic system to its “linear” form, with respect to quadratic terms. Consider the vector
and the quadratic expression
where \({{{{\textbf {{\texttt {P}}}}}}} \in \mathbb {R}^{4\times 4}\). We can reformulate Eq. (76) to its “linear” form as
In the next sections we will focus once more on describing all constraints in their natural quadratic form, always with the outlook that the previous reformulation can be applied and that each quadratic constraint will contribute a row in the final linear system in Eq. (74).
1.2 D.2 Orthogonality of Columns
We start by writing Eq. (71) in a more compact linear form
where
The first important step is to define an operation which allows us to select each column of \({{{{\textbf {{\texttt {R}}}}}}}\). Using the index i to designate the desired column, we can write
With this mechanism in place, orthogonality of the columns reads
Substituting the appropriate terms
Considering all indices
which contributes 6 equations to the system in Eq. (74).
1.3 D.3 Orthogonality of Rows
Similarly to the previous section, we start by defining a selector operator which allows us to isolate the rows of \({{{{\textbf {{\texttt {R}}}}}}}\) from \({\textbf{r}}\). Not surprisingly, we can verify that this operator can be built by commuting both terms in the Kronecker product.
With this operator in place, orthogonality of the rows reads
Substituting the appropriate terms
Considering all indices
which contributes 6 additional equations to the system in Eq. (74).
1.4 D.4 Determinant - Right Hand Convention
Reusing the column selector operator from Eq. (81), the right-hand convention specifies that
for \((i, j, k) \in \{(1, 2, 3), (2, 3, 1), (3, 1, 2)\}\). We resort to the unit vector \({\textbf{e}}_l\) to specify the constraint with respect to each individual component. We will also exploit the cross product identity,
Starting with
Considering all indices, we have
with \((i, j, k) = \{(1, 2, 3), (2, 3, 1), (3, 1, 2)\}, l = \{1, 2, 3\}\), for a total of 9 equations.
Distribution of the ten eigenvalues of \({{{{{\textbf {{\texttt {Z}}}}}}}}\) for minimal (P3L and P3L) and non-minimal (P8P and P8L) scenarios under noiseless conditions, over 1000 runs. The red horizontal line represents the rank threshold used of 0.001. The box upper and lower bounds plus the orange line, mark the three quartiles of the distribution, and the whiskers mark the 5th and 95th percentiles
Appendix E The Splitting Conic Solver
The Splitting Conic Solver (SCS) [29] makes use of a first-order method for solving large-scale primal-dual convex cone programs. The method relies on the Alternating Direction Method of Multipliers (ADMM) [4] to solve the homogeneous self-dual embedding. The homogeneous self-dual embedding [44] is an equivalent feasibility problem to the original primal-dual cone program, that consists in finding a nonzero point resultant from the the intersection of a cone and an affine set. At each iteration the solver solves a system of linear equations and projects a point onto the cone. The solver returns solutions to the primal and dual problems, that we leverage to certify the optimality of the solutions returned by CvxPnPL. When not available,it alternatively provides a certificate of infeasibility or unboundedness. The method is particularly suited for large-scale problems where interior point methods are too slow.
Appendix F Rank Threshold Selection Criterion and Sensitivity
In this section, we provide some additional results supporting our statement on CvxPnPL not requiring accurate rank estimates, that are dependent on the rank threshold. This threshold is used decide whether a given eigenvalue counts towards the rank of \({{{{\textbf {{\texttt {Z}}}}}}}\). CvxPnPL is able to gracefully handle rank overestimates as is shown in Table 3. However, by setting an extremely low rank threshold, one is throwing away the reduced computational benefit from handling lower rank cases. We picked the rank threshold of 0.001 supported by numerical experiments similar to the setuo in Sect. 7.1, but using minimal and non-minimal PnP and PnL scenarios. As show in Fig. 9, minimal scenarios with 3 points or lines have multiple solutions and produce higher eigenvalues for \({{{{\textbf {{\texttt {Z}}}}}}}\), while for non-minimal scenarios, e.g., 8 points or lines scenarios, there’s a single valid solution and lower eigenvalues. CvxPnPL can only handle situations up to rank 4 so the threshold is set to ensure that the 4 largest “non-null” eigenvalues are comfortably above it.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Agostinho, S., Gomes, J. & Del Bue, A. CvxPnPL: A Unified Convex Solution to the Absolute Pose Estimation Problem from Point and Line Correspondences. J Math Imaging Vis 65, 492–512 (2023). https://doi.org/10.1007/s10851-022-01133-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10851-022-01133-8