Skip to main content
Springer Nature Link
Log in

Penalty guided genetic search for redundancy optimization in multi-state series-parallel power system

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

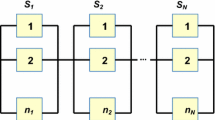
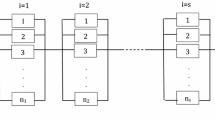
This paper presents a genetic algorithm (GA) for parallel redundancy optimization in series-parallel power systems exhibiting multi-state behavior, optimizing the reliability subject to constraints. The components are binary and chosen from a list of products available in the market, and are being characterized by their feeding capacity, reliability, cost and weight. System reliability is defined as the ability to satisfy consumer demand and is presented as a piecewise cumulative load curve.

In GA, to handle infeasible solutions penalty strategies are used. Penalty technique keep a certain amount of infeasible solutions in each generation so as to enforce genetic search towards an optimal solution from sides of, both, feasible and infeasible regions. We here present a dynamic adaptive penalty function which helps the algorithm to search efficiently for optimal/near optimal solution. To evaluate system reliability, a fast procedure, based on universal generating function, is used. An example considering a multi-state series-parallel power system is solved considering both homogeneous and heterogeneous types of redundancy. Also an example considering price discounts is solved. The effectiveness of the penalty function and the proposed algorithm is studied and shown graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Agarwal M, Gupta R (2004) Genetic search for redundancy optimization in complex systems. In: Proc. Advanced Reliability Modeling (AIWARM 2004), Hiroshima Japan, pp 1–8, Full version of the paper to appear in Journal of Quality in Maintenance Engineering

  • Aggarwal S, Agarwal M, Gupta R (2005) A Heuristic approach for constrained redundancy optimization in multi-state systems. To appear in EQC (Int J Qual Reliab)

  • Aven T (1985) Reliability evaluation of multistate systems with multistate components. IEEE Trans Reliab 34(5):473–479

    MATH  MathSciNet  Google Scholar 

  • Aven T (1993) On performance measures for multistate monotone systems. Reliab Engi Syst Saf 41:259–266

    Article  Google Scholar 

  • Barlow RE, Wu AS (1978) Coherent systems with multistate components. Math Oper Res 3:275–281

    MATH  MathSciNet  Google Scholar 

  • Bazarra MS, Sherali HD, Shetty CM (1979) Nonlinear programming: theory and algorithms. John Wiley and Sons, Inc, New York, USA

    Google Scholar 

  • Billinton R, Allan R (1984) Reliability of power systems. Pitman, London, UK

    Google Scholar 

  • Chen C, Meng M, Zuo M (1999) Selective maintenance optimization for multi-state systems. In: Proceedings of the 1999 IEEE Canadian Conference on Electrical and Computer Engineering, Edmonton, Alberta, Canada

  • Coit DW, Smith AE (1996a) Reliability optimization of series-parallel systems using a genetic algorithm. IEEE Trans Reliab 45:254–260

    Google Scholar 

  • Coit DW, Smith AE (1996b) Penalty guided genetic search for reliability design optimization. Comput Ind Engi 30:895–904

    Article  Google Scholar 

  • Coit DW, Smith AE, Tate DM (1996) Adaptive penalty methods for genetic optimization of constrained combinatorial problems. INFORMS J Comput 8:173–182

    Article  MATH  Google Scholar 

  • Deeter DL, Smith AE (1997) Heuristic optimization of network design considering all terminal reliability. In: Mcafee NJ (ed) Proceedings Annual Reliability and Maintainability Symposium, Philadelphia, PA, pp 194–199

  • Dengiz B, Altiparmak F, Smith AE (1997) Local search genetic algorithm for optimal design of reliable networks. IEEE Trans Evol Comput 1:179–188

    Article  Google Scholar 

  • El-Neveihi E, Proschan F, Seturaman J (1978) Multistate coherent systems. J. Appl Probab 15:675–688

    Article  MathSciNet  Google Scholar 

  • El-Neveihi E, Proschan F, Setharaman J (1988) Optimal allocation of multistate elements. In: Krishnaiah P (ed), Handbook of statistics, Elsevier Science Publishers vol. 7 pp 427–432

  • Fiacco AV, McCormick GP (1968) Nonlinear programming: sequential unconstrained minimization techniques. John Wiley and Sons, Inc, New York USA

    MATH  Google Scholar 

  • Gen M, Cheng R (1997) Genetic algorithms and engineering design. John Wiley and Sons, Inc, New York, USA

  • Goldberg DE (1989) Genetic algorithms in search, optimization and machine learning. Reading MA, Addison-Wesley

  • Holland J (1975) Adaptation in natural and artificial systems. University of Michigan Press

  • Hsieh YC, Chen TC, Bricker DL (1997) Genetic algorithms for reliability design problems. Technical Report, Dept. of Industrial Engineering, University of Iowa

  • Ida K, Gen M, Yokta T (1996) System relaibility optimization of series-parallel systems using a genetic algorithm. IEEE Trans Reliab 45:254–260

    Google Scholar 

  • Kumar A, Pathak RM, Gupta YP (1995) Genetic-algorithm-based reliability optimization for computer network expansion. IEEE Trans Reliab 44:63–72

    Article  Google Scholar 

  • Kuo W, Rajendra VP, Tillman FA, Hwang CL (2001) Optimal reliability design—fundamentals and applications. Cambridge University Press, Cambridge

    Google Scholar 

  • Levitin G, Lisnianski A, Elmakis D (1997) Structure optimization of power system with different redundant elements. Electr Power Syst Res 43(1):19–27

    Article  Google Scholar 

  • Levitin G, Lisnianski A, Haim HB, Elmakis D (1998) Redundancy optimization for series-parallel multistate systems. IEEE Trans Reliab 47(2):165–172

    Google Scholar 

  • Lin CY, Wu WH (2004) Self-organizing adaptive penalty strategy in constrained genetic search. Struct Multidisc Optim 26:417–428

    Article  Google Scholar 

  • Lisnianski A, Levitin G, Haim HB, Elmakis D (1996) Power system structure optimization subject to reliability constraints. Electr Power Syst Res 39(2):145–152

    Article  Google Scholar 

  • Lisnianski A, Levitin G (2003) Multistate system reliability- assessment, optimization and applications. World Scientific Publishing Co. Pte. Ltd., Singapore

    Google Scholar 

  • Majety SRV, Rajgopal J (1997) Dynamic penalty function for evolutionary algorithms with an application to reliability allocation. Technical Report, Dept. of Industrial Engineering, University of Pittsburgh, Pittsburgh, PA

  • Meng F (1996) More on optimal allocation of elements in coherent systems. J Appl Probab 33:548–556

    Article  MATH  MathSciNet  Google Scholar 

  • Michalewicz Z (1995) Genetic algorithms, numerical optimization, and constraints. In Proc. of 6th Int. Conf. on Genetic Algorithms, pp 151–158

  • Painton L, Campbell J (1995) Genetic algorithms in optimization of system reliability. IEEE Trans Reliab 44:172–178

    Article  Google Scholar 

  • Rakowsky UK (2005) On multi-system reliability and operation. In: Advances in safety and reliability (ESREL 2005), Vol-II, (Editor) Krzysztof Kolowrocki, Taylor & Francis Group plc, London, UK, pp 1637–1643

  • Ramirez-Marquez JE, Coit DW (2004) A heuristic for solving the redundancy allocation problem for multistate series-parallel systems. Reliab Eng Sys Saf 83:341–349

    Google Scholar 

  • Ramirez-Marquez JE, Coit DW (2005) Multi-state component criticality analysis in multi-state systems. In: Advances in safety and reliability (ESREL 2005), Vol-II, (Editor) Krzysztof Kolowrocki, Taylor & Francis Group plc, London, UK, pp 1671–1677

  • Reeves CR (1993) Modern heuristic techniques for combinatorial problems. Orient Longman

  • Ross SM (1979) Multivalued state component systems. Ann Probab 7:379–383

    MATH  MathSciNet  Google Scholar 

  • Smith AE, Coit DW (1995) Handbook of Evolutionary Computation, Section C 5.2, Penalty Functions, Joint Publication of Oxford University Press and Institute of Physics Publishing

  • Tian Z, Zuo MJ (2005) Reliability-redundancy allocation for multi-state series-parallel systems. In: Advances in safety and reliability (ESREL 2005), Vol-II, (Editor) Krzysztof Kolowrocki, Taylor & Francis Group plc, London UK, pp 1925–1930

  • Ushakov I (1986) A universal generating function. Soviet Journal Computer Systems Science 61–73

  • Ushakov I (1987) Optimal standby problems and a universal generating function. Soviet J Com Sys Sci 25(4):79–82

    MATH  MathSciNet  Google Scholar 

  • Ushakov I (1988) Reliability analysis of multistate systems by means of modified generating function. Journal Information Process. Cybernet 24(3):131–135

    MATH  MathSciNet  Google Scholar 

  • Wood AP (1985) Multi-state block diagrams and fault trees. IEEE Trans. on Reliability 34(3): 236–240

    Article  Google Scholar 

  • Wu WH, Lin CY (2004) The second generation of self-organizing adaptive penalty strategy for constrained genetic search. Adv Eng Softw 35(12):815–825

    MATH  Google Scholar 

  • Yokota T, Gen M, Ida K (1995) System reliability of optimization problems with several failure modes by genetic algorithm. Japan J Fuzzy Theory Syst 7(1):117–135

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Operational Research, University of Delhi, Delhi, 110007, India

    Rashika Gupta & Manju Agarwal

Authors
  1. Rashika Gupta
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Manju Agarwal
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Manju Agarwal.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Gupta, R., Agarwal, M. Penalty guided genetic search for redundancy optimization in multi-state series-parallel power system. J Comb Optim 12, 257–277 (2006). https://doi.org/10.1007/s10878-006-9632-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-006-9632-1

Keywords