Abstract
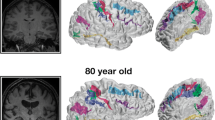
We describe geometric invariants that characterize the shape of curves and surfaces in 3D space: curvature, Gauss integrals and moments. We apply these invariants to neuroimaging data to determine if they have application for automatically classifying and parcellating cortical data. The curves of sulci and gyri on the cortical surface can be obtained by reconstructing cortical surface representations of the human brain from magnetic resonance imaging (MRI) data. We reconstructed gray matter surfaces for 15 subjects, traced 10 sulcal curves on each surface and computed geometric invariants for each curve. These geometric features were used classify the curves into sulcal and hemispheric classes. The best classification results were obtained when moment-based features were computed on the sulcal curves in native space. Gauss integral measures showed that they were useful for differentiating the hemispheric location of a single sulcus. These promising results may indicate that moment invariants are useful for characterizing shape on a global scale. Gauss integral invariants are potentially useful measures for characterizing cortical shape on a local, rather than global scale. Gauss integrals have found biological significance in characterizing proteins so it is worthwhile to consider their possible application to neuroscientific data.
Similar content being viewed by others
References
Crick FH (1976) Linking numbers and nucleosomes. Proc Natl Acad Sci USA 73:2639–2643
Dale AM, Fischl B, Sereno MI (1999) Cortical surface-based analysis, I: segmentation and surface reconstruction. NeuroImage 9:179–194
Dijkstra EW (1959) A note on two problems in connection with graphs. Numer Math 1:269–271
doCarmo MP (1976) Differential geometry of curves and surfaces. Prentice Hall, Englewood Cliffs
Duda RO, Stork DG, Hart PE (1999) Pattern classification. Wiley, Indianapolis
Fuller F (1971) The writhing number of a space curve. Proc Natl Acad Sci USA 68(4):815–819
Gremban KD, Miller GL, Teng SH (1997) Moments of inertia and graph separators. J Comb Optim 1(1):79–104
Hamann B (1993) Curvature approximation for triangulated surfaces. In: Farin G, Hagen H, Noltemeier H (eds) Geometric modelling in computing supplementum 8. Springer, New York, pp 139–153
Hu MK (1962) Visual pattern recognition by moment invariants. IRE Trans Inf Theory 8:179–187
Jolliffe IT (2002) Principal component analysis. Springer, New York
LaConte S, Anderson J, Muley S, Ashe J, Frutiger S, Rehm K, Hansen LK, Yacoub E, Hu X, Rottenberg D, Strother S (2003) The evaluation of preprocessing choices in single-subject BOLD fMRI using NPAIRS performance metrics. NeuroImage 18:10–27
Laing C, Sumners DW (2006) Computing the writhe on lattices. J Phys A: Math Gen 39:3535–3543
Lipschultz MM (1980) Differential geometry. Schaum’s outline series. McGraw–Hill, New York
Lo C-H, Don H-S (1989a) 3D moments forms: their construction and application to object identification and positioning. IEEE Trans Pattern Anal Mach Intell 11(10):1053–1064
Lo C-H, Don H-S (1989b) Representation and recognition of 3D curves. In: Proceedings IEEE computer society conference on computer vision and pattern recognition. IEEE, New York, pp 523–528
Lo C-H, Don H-S (1990) Pattern recognition using 3D moments. In: The tenth international conference on pattern recognition. IEEE, New York, pp 540–544
Lyoo LF, Sung YH, Dager SR, Friedman SD, Lee JY, Kim SJ, Kim N, Dunner DL, Renshaw PF (2006) Regional cerebral cortical thinning in biopolar disorder. Bipolar Disord 8:65–74
Mangin J-F, Poupon F, Duchesnay E, Rivière D, Cachia A, Collinse DL, Evans A, Régis J (2004) Brain morphometry using 3D moment invariants. Med Image Anal 8:187–196
Martinussen M, Fischl B, Larsson HB, Skranes J, Kulseng S, Vangberg TR, Vik T, Brubakk AM, Haraldseth O, Dale AM (2005) Cerebral cortex thickness in 15-year-old adolescents with low birth weight measured by an automated MRI-based method. Brain 128:2588–2596
McHugh JA (1990) Algorithmic graph theory. Prentice Hall, Englewood Cliffs
McLachlan GJ (1992) Discriminant analysis and statistical pattern recognition. Wiley, New York
Milad MR, Quinn BT, Pitman RK, Orr SP, Fischl B, Rauch SL (2005) Thickness of ventromedial prefrontal cortex in humans is correlated with extinction memory. Proc Nat Acad Sci USA 102:10706–10711
Ono M, Kubik S, Chad A (1990) Atlas of the cerebral sulci. Thieme, Stuttgart
Orengo CA, Michie AD, Jones S, Jones DT, Swindells MB, Thornton JM (1997) CATH—a hierarchic classification of protein domain structures. Structure 5:1093–1108
Pohl WF (1980) DNA and differential geometry. Math Int 3:20–27
Ratnanather JT, Barta PE, Honeycutt NA, Lee NG, Morris HM, Dziorny AC, Hurdal MK, Pearlson GD, Miller MI (2003) Dynamic programming generation of boundaries of local coordinatized submanifolds in the neocortex: application to the planum temporale. NeuroImage 20:359–377
Rogen P, Bohr H (2003) A new family of global protein shape descriptors. Math Biosci 182:167–181
Rogen P, Fain B (2003) Automatic classification of protein structure by using Gauss integrals. Proc Natl Acad Sci USA 100(1):119–124
Shiraishi H, Ahlfors SP, Stufflebeam SM, Takano K, Okajima M, Knake S, Hatanaka K, Kohsaka S, Saitoh S, Dale AM, Halgren E (2005) Application of magnetoencephalography in epilepsy patients with widespread spike or slow-wave activity. Epilepsia 46:1264–1272
Thirion JP, Gourdon A (1996) The 3D marching lines algorithm and its application to crest lines extraction. Graph Model Image Process 58:503–509
Witten IH, Frank E (2005) Data mining: practical machine learning tools and techniques, 2nd edn. Kaufmann, San Francisco
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hurdal, M.K., Gutierrez, J.B., Laing, C. et al. Shape analysis for automated sulcal classification and parcellation of MRI data. J Comb Optim 15, 257–275 (2008). https://doi.org/10.1007/s10878-007-9096-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-007-9096-y