Abstract
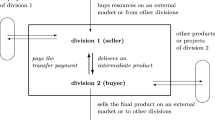
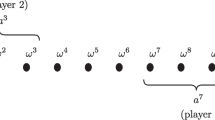
If resources and facilities from different partners need to be engaged for a large-scale project with a huge number of tasks, any of which is indivisible, decision on the number of tasks assigned to any collaborating partner often requires a certain amount of coordination and bargaining among these partners so that the ultimate task allocation can be accepted by any partner in a business union for the project. In the current global financial crisis, such cases may appear frequently. In this paper, we first investigate the behavior of such a discrete bargaining model often faced by service-based organizations. In particular, we address the general situation of two partners, where the finite Pareto efficient (profit allocation) set does not possess any convenient assumption for deriving a bargaining solution, namely a final profit allocation (corresponding to a task assignment) acceptable to both partners. We show that it is not appropriate for our discrete bargaining model to offer the union only one profit allocation. Modifying the original optimization problem used to derive the Nash Bargaining Solution (NBS), we develop a bargaining mechanism and define a related bargaining solution set to fulfil one type of needs on balance between profit-earning efficiency and profit-earning fairness. We then show that our mechanism can also suit both Nash’s original concave bargaining model and its continuous extension without the concavity of Pareto efficient frontier on profit allocation.
Similar content being viewed by others
References
Anant TCA, Mukherji B, Basu K (1990) Bargaining without convexity: generalizing the Kalai–Smorodinsky solution. Economics 33(2):115–119
Cao XR (1982) Preference functions and bargaining solutions. In: Proc IEEE conf decision and control, pp 164–171
Cao XR, Shen H, Milito R, Wirth P (2002) Internet pricing with a game theoretical approach: concepts and examples. IEEE/ACM Trans Netw 10:208–216
Chen QL, Cai XQ (2004) Application on NBS for a negotiable third-party scheduling problem with a due window. In: ICSSSM 2004, pp 116–119
Chen QL (2006) A new discrete bargaining model on job partition between two manufacturers. PhD diss, Faculty of Engineering, The Chinese University of Hong Kong, Hong Kong
Chen QL, Cai XQ, Gu YH (2006) An optimization problem on two-partition of jobs for profit allocation. In: APCCAS 2006, pp 626–629
Conley J, Wilkie S (1991) The bargaining problem without convexity: extending the egalitarian and Kalai–Smorodinsky solutions. Econ Lett 36:365–369
Dagan N, Volij O, Winter E (2002) A characterization of the Nash bargaining solution. Soc Choice Welf 19:811–823
Dong L, Liu H (2007) Equilibrium forward contracts on nonstorable commodities in the presence of market power. Oper Res 55:128–145
Gan XB, Gu YH, Vairaktarakis GL, Cai XQ, Chen QL (2007) A scheduling problem with one producer and the bargaining counterpart with two producers. In: ESCAPE 2007, pp 305–316
Gurnani N, Shi MZ (2006) A bargaining model for a first-time interaction under asymmetric beliefs of supply reliability. Manag Sci 52:865–880
Herrero MJ (1989) The Nash program: nonconvex bargaining problems. J Econ Theory 49:266–277
Kalai E, Smorodinsky M (1975) Other solutions to Nash’s bargaining problems. Econometrica 43:513–518
Lahiri S (2004) Axiomatic characterization of the Nash and Kalai–Smorodinsky solutions for discrete bargaining problems. Pure Math Appl 14:207–220
Mariotti M (1998) Nash bargaining theory when the number of alternatives can be finite. Soc Choice Welf 15:413–421
Muthoo A (1999) Bargaining theory with applications. Cambridge University Press, Cambridge
Nagahisa R, Tanaka M (2002) An axiomatization of the Kalai–Smorodinsky solution when the feasible sets can be finite. Soc Choice Welf 19:751–761
Nash JF (1950) The bargaining problem. Econometrica 18:155–162
Nash JF (1953) Two person cooperative games. Econometrica 21:128–140
Raiffa H (1953) Arbitration schemes for generalized two-person games. In: Kuhn HW, Tucker AW (eds) Contributions to the theory of game II. Princeton University Press, Princeton, pp 361–387
Saaty TL (1980) The analytic hierarchy process: planning, priority setting, resource allocation. McGraw-Hill, New York
Thomson W (1981) Nash’s bargaining solution and utilitarian choice rules. Econometrica 49:535–538
Touati C, Altman E, Galtier J (2006) Generalized Nash bargaining solution for bandwidth allocation. Comput Netw 50:3242–3263
Trockel W (2002) Integrating the Nash program into mechanism theory. Rev Econ Des 7:27–43
Trockel W (2005) Core-equivalence for the Nash bargaining solution. Econ Theory 25:255–263
Zhang D (2005) A logical model of Nash bargaining solution. In: IJCAI, pp 983–990
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gu, Y.H., Goh, M., Chen, Q.L. et al. A new two-party bargaining mechanism. J Comb Optim 25, 135–163 (2013). https://doi.org/10.1007/s10878-011-9424-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-011-9424-0