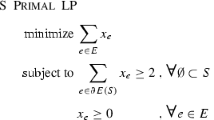Abstract
Given a directed simple graph \(G=(V,E)\) and a cost function \(c:E \rightarrow R_+\), the power of a vertex \(u\) in a directed spanning subgraph \(H\) is given by \(p_H(u) = \max _{uv \in E(H)} c(uv)\), and corresponds to the energy consumption required for wireless node \(u\) to transmit to all nodes \(v\) with \(uv \in E(H)\). The power of \(H\) is given by \(p(H) = \sum _{u \in V} p_H(u)\). Power Assignment seeks to minimize \(p(H)\) while \(H\) satisfies some connectivity constraint. In this paper, we assume \(E\) is bidirected (for every directed edge \(e \in E\), the opposite edge exists and has the same cost), while \(H\) is required to be strongly connected. Moreover, we assume \(c:E \rightarrow \{A,B\}\), where \(0 \le A < B\). We improve the best known approximation ratio from 1.75 (Chen et al. IEEE GLOBECOM 2005) to \(\pi ^2/6 - 1/36 + \epsilon \le 1.61\) using an adaptation of the algorithm developed by Khuller et al. [SIAM J Comput 24(4):859–872 1995, Discr Appl Math 69(3):281–289 1996] for (unweighted) Minimum Strongly Connected Subgraph.









Similar content being viewed by others
References
Alon N, Yuster R, Zwick U (1995) Color-coding. J ACM 42(4):844–856
Althaus E, Calinescu G, Mandoiu I, Prasad S, Tchervenski N, Zelikovsky A (2006) Power efficient range assignment for symmetric connectivity in static ad hoc wireless networks. Wirel Netw 12(3):287–299
Calinescu G (2010) Min-power strong connectivity. In Serna M, Jansen K, Rolin J (eds). In: Proceedings of the international workshop on approximation algorithms for combinatorial optimization, number 6302 in Lecture Notes in Computer Science, Springer, pp 67–80
Calinescu G, Kapoor S, Olshevsky A, Zelikovsky A (2003) Network lifetime and power assignment in ad-hoc wireless networks. In: Proceedings 11th European Symphosium on Algorithms, pp 114–126
Calinescu G (2013) Approximate min-power strong connectivity. SIAM J Discr Math to appear
Caragiannis I, Kaklamanis C, Kanellopoulos P (2006) Energy-efficient wireless network design. Theor Comput Syst 39(5):593–617
Carmi P, Katz MJ (2007) Power assignment in radio networks with two power levels. Algorithmica 47(2):183–201
Chen J-J, Lu H-I, Kuo T-W, Yan C-Y, Pang A-C (2005) Dual power assignment for network connectivity in wireless sensor networks. In: IEEE Global Telecommunications Conference, 2005. GLOBECOM ’05. vol 6, pp 3638–3642
Chen J, Lu S, Sze S-H, Zhang F (2007) Improved algorithms for path, matching, and packing problems. In: N Bansal, K Pruhs, C Stein (eds) SODA, pp 298–307, SIAM
Chen WT, Huang NF (1989) The strongly connecting problem on multihop packet radio networks. IEEE Trans Commun 37(3):293–295
Clementi AEF, Penna P, Silvestri R (2004) On the power assignment problem in radio networks. MONET 9(2):125–140
Cormen Thomas H, Leiserson Charles E, Rivest Ronald L, Stein Clifford (2009) Introduction to algorithms, 3rd edn. The MIT Press, Cambridge
Gabow HN, Stallmann M (1985) Efficient algorithms for graphic matroid intersection and parity. In: 12th colloqium on automata, language and programming, pp 210–220
Graham RL, Grötschel M, Lovász L (eds) (1995) Handbook of combinatorics, vol 1–2. Elsevier Science B.V., Amsterdam
Grandoni F (2012) On min-power Steiner tree. In: Epstein L, Ferragina P (eds) Lecture notes in computer science, vol 7501., ESASpringer, Berlin, pp 527–538
Hajiaghayi MT, Immorlica N, Mirrokni VS (2003) Power optimization in fault-tolerant topology control algorithms for wireless multi-hop networks. In: MOBICOM, pp 300–312
Jothi Raja, Raghavachari Balaji, Varadarajan Jothi R, Ragavachari B, Varadarajan S (2003) A 5/4-approximation algorithm for minimum 2-edge-connectivity. In: SODA ’03: Proceedings of the fourteenth annual ACM-SIAM symposium on discrete algorithms, pp 725–734, Society for Industrial and Applied Mathematics, Philadelphia
Khuller S, Raghavachari B, Young N (1995) Approximating the minimum equivalent digraph. SIAM J Comput 24(4):859–872
Khuller S, Raghavachari B, Young N (1996) On strongly connected digraphs with bounded cycle length. Discrete Appl Math 69(3):281–289
Koutis I (2008) Faster algebraic algorithms for path and packing problems. In: Aceto L, Damgård I, Goldberg LA, Halldórsson MM, Ingólfsdóttir A, Walukiewicz I (eds) Lecture notes in computer science, vol 5125., ICALP (1)Springer, Berlin
Krumke S, Liu R, Lloyd E, Marathe M, Ramanathan R, Ravi SS (2003) Topology control problems under symmetric and asymmetric power thresholds. In: Proceedings of Ad-Hoc Now, pp 187–198
Lovász L, Plummer MD (1986) Matching theory. Elsevier, Amsterdam
Nutov Z, Yaroshevitch A (2009) Wireless network design via 3-decompositions. Inf Process Lett 109(19):1136–1140
Ramanathan Ram, Rosales-Hain Regina (2000) Topology control of multihop wireless networks using transmit power adjustment. INFOCOM 2:404–413
Szigeti Z (2003) On the graphic matroid parity problem. J Combin Theory Ser B 88:247–260
Vetta A (2001) Approximating the minimum strongly connected subgraph via a matching lower bound. In: SODA ’01: Proceedings of the twelfth annual ACM-SIAM symposium on discrete algorithms, pp 417–426, Industrial and Applied Mathematics, Philadelphia
Wattenhofer R, Li L, Bahl P, Wang Y-M (2001) Distributed topology control for wireless multihop ad-hoc networks. In: IEEE INFOCOM’01
Acknowledgments
Research supported in part by NSF Grants CCF-0515088 and NeTS-0916743.
Author information
Authors and Affiliations
Corresponding author
Additional information
These results appeared in a preliminary version in the proceedings of the International Workshop on Approximation Algorithms for Combinatorial Optimization (APPROX 2010).
Rights and permissions
About this article
Cite this article
Călinescu, G. 1.61-approximation for min-power strong connectivity with two power levels. J Comb Optim 31, 239–259 (2016). https://doi.org/10.1007/s10878-014-9738-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-014-9738-9