A $(3,1)^{*}$-choosable theorem on planar graphs

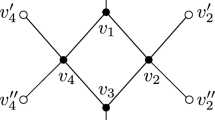
Abstract

A list assignment of a graph G is a function L that assigns a list L(v) of colors to each vertex $v\in V(G)$. An $(L,d)^*$-coloring is a mapping $\pi$ that assigns a color $\pi (v)\in L(v)$ to each vertex $v\in V(G)$ so that at most d neighbors of v receive color $\pi (v)$. A graph G is said to be $(k,d)^*$-choosable if it admits an $(L,d)^*$-coloring for every list assignment L with $|L(v)|\ge k$ for all $v\in V(G)$. In this paper, we prove that every planar graph with neither adjacent triangles nor 6-cycles is $(3,1)^*$-choosable. This is a partial answer to a question of Xu and Zhang (Discret Appl Math 155:74–78, 2007) that every planar graph without adjacent triangles is $(3,1)^*$-choosable. Also, this improves a result in Lih et al. (Appl Math Lett 14:269–273, 2001) which says that every planar graph without 4- and 6-cycles is $(3,1)^*$-choosable.