Abstract
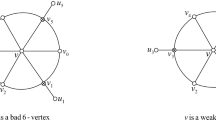
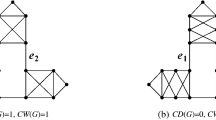
The vertex arboricity va(G) of a graph G is the minimum number of colors the vertices can be colored so that each color class induces a forest. It was known that \(va(G)\le 3\) for every planar graph G. In this paper, we prove that \(va(G)\le 2\) if G is a planar graph without intersecting 5-cycles.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Chartrand G, Kronk HV (1969) The point-arboricity of planar graphs. J Lond Math Soc 44:612–616
Chartrand G, Kronk HV, Wall CE (1968) The point-arboricity of a graph. Israel J Math 6:169–175
Chen M, Raspaud A, Wang WF (2012) Vertex-arboricity of planar graphs without intersecting triangles. Eur J Combin 33:905–923
Choi I, Zhang HH (2014) Vertex arboricity of toroidal graphs with a forbidden cycle. Discrete Math 333:101–105
Fijavž G, Juvan M, Mohar B, Škrekovski R (2002) Planar graphs without cycles of specific lengths. Eur J Combin 23:377–388
Huang DJ, Wang WF (2013) Vertex arboricity of planar graphs without chordal 6-cycles. Int J Comput Math 90:258–272
Huang DJ, Shiu WC, Wang WF (2012) On the vertex-arboricity of planar graphs without 7-cycles. Discrete Math 312:2304–2315
Huang F, Wang XM, Yuan JJ (2014) On the vertex-arboricity of \(K_5\)-minor-free graphs of diameter 2. Discrete Math 322:1–4
Raspaud A, Wang WF (2008) On the vertex-arboricity of planar graphs. Eur J Combin 29:1064–1075
Roychoudhury A, Sur-Kolay S (1995) Efficident algorithms for vertex arboricity of planar graph. Foundations of software technology and theoretical computer science, vol 1026. Springer, Berlin, pp 37–51
Wang WF, Lih K-W (2002) Choosability and edge choosability of planar graphs without five cycles. Appl Math Lett 15:561–565
Author information
Authors and Affiliations
Corresponding author
Additional information
This work is supported by NSFC (11271006, 11631014), XJEDU2016I046 and XJEDU2014S067 of China.
Rights and permissions
About this article
Cite this article
Cai, H., Wu, J. & Sun, L. Vertex arboricity of planar graphs without intersecting 5-cycles. J Comb Optim 35, 365–372 (2018). https://doi.org/10.1007/s10878-017-0168-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-017-0168-3