Algorithm complexity of neighborhood total domination and $(\rho ,\gamma _{nt})$-graphs

Abstract

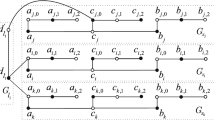
A neighborhood total dominating set, abbreviated for NTD-set D, is a vertex set of G such that D is a dominating set with an extra property: the subgraph induced by the open neighborhood of D has no isolated vertex. The neighborhood total domination number, denoted by $\gamma _{nt}(G)$, is the minimum cardinality of a NTD-set in G. In this paper, we prove that NTD problem is NP-complete for bipartite graphs and split graphs. Then we give a linear-time algorithm to determine $\gamma _{nt}(T)$ for a given tree T. Finally, we characterize a constructive property of $(\gamma _{nt},2\gamma )$-trees and provide a constructive characterization for $(\rho ,\gamma _{nt})$-graphs, where $\gamma$ and $\rho$ are domination number and packing number for the given graph, respectively.