Skip to main content
Springer Nature Link
Log in

Asymptotically optimal policy for stochastic job shop scheduling problem to minimize makespan

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

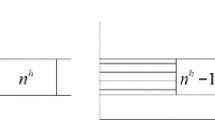
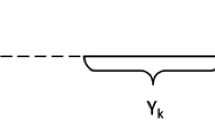
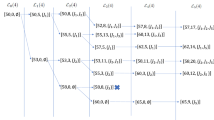
This paper studies the large-scale stochastic job shop scheduling problem with general number of similar jobs, where the processing times of the same step are independently drawn from a known probability distribution, and the objective is to minimize the makespan. For the stochastic problem, we introduce the fluid relaxation of its deterministic counterpart, and define a fluid schedule for the fluid relaxation. By tracking the fluid schedule, a policy is proposed for the stochastic job shop scheduling problem. The expected value of the gap between the solution produced by the policy and the optimal solution is proved to be O(1), which indicates the policy is asymptotically optimal in expectation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Bertsimas D, Gamarnik D (1999) Asymptotically optimal algorithms for job shop scheduling and packet routing. J Algorithms 33:296–318

    Article  MathSciNet  MATH  Google Scholar 

  • Bertsimas D, Sethuraman J (2002) From fluid relaxations to practical algorithms for job shop scheduling: the makespan objective. Math Program 92(1):61–102

    Article  MathSciNet  MATH  Google Scholar 

  • Bertsimas D, Gamarnik D, Sethuraman J (2003) From fluid relaxations to practical algorithms for high-multiplicity job-shop scheduling: the holding cost objective. Oper Res 51(5):798–813

    Article  MathSciNet  MATH  Google Scholar 

  • Boudoukh T, Penn M, Weiss G (2001) Scheduling jobshops with some identical or similar jobs. J Sched 4:177–199

    Article  MathSciNet  MATH  Google Scholar 

  • Boudoukh T, Penn M, Weiss G (1998) Job-shop an application of fluid approximation. In: Gilad I (ed) Proceedings of the tenth conference of industrial engineering and management, pp 254–258, June 1998, Haifa Israel

  • Dai JG, Weiss G (2002) A fluid heuristic for minimizing makespan in job shops. Oper Res 50(4):692–707

    Article  MathSciNet  MATH  Google Scholar 

  • Gu M, Lu X (2011) Asymptotical optimality of WSEPT for stochastic online scheduling on uniform machines. Ann Oper Res 191(1):97–113

    Article  MathSciNet  MATH  Google Scholar 

  • Gu M, Lu X (2013) The expected asymptotical ratio for preemptive stochastic online problem. Theor Comput Sci 495:96–112

    Article  MathSciNet  MATH  Google Scholar 

  • Masin M, Raviv T (2014) Linear programming-based algorithms for the minimum makespan high multiplicity jobshop problem. J Sched 17:321–338

    Article  MathSciNet  MATH  Google Scholar 

  • Nazarathy Y, Weiss G (2010) A fluid approach to large volume job shop scheduling. J Sched 13:509–529

    Article  MathSciNet  MATH  Google Scholar 

  • Penn M, Raviv T (2009) An algorithm for the maximum revenue jobshop problem. Eur J Oper Res 193:437–450

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China (Grant Nos. 11201282 and 61304209), Humanity and Social Science Foundation of Ministry of Education of China (Grant No. 17YJAZH024).

Author information

Authors and Affiliations

  1. College of Economics and Management, Shanghai University of Electric Power, Shanghai, 200090, China

    Jinwei Gu

  2. Institute of Scientific Computation and Financial Data Analysis, School of Mathematics, Shanghai University of Finance and Economics, Shanghai, 200433, China

    Manzhan Gu

  3. Department of Mathematics, East China University of Science and Technology, Shanghai, 200237, China

    Xiwen Lu

  4. School of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA, 30332, USA

    Ying Zhang

Authors
  1. Jinwei Gu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Manzhan Gu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiwen Lu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Ying Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Manzhan Gu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gu, J., Gu, M., Lu, X. et al. Asymptotically optimal policy for stochastic job shop scheduling problem to minimize makespan. J Comb Optim 36, 142–161 (2018). https://doi.org/10.1007/s10878-018-0294-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-018-0294-6

Keywords