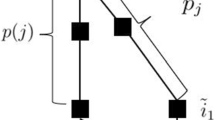
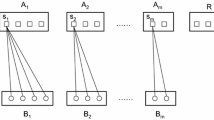
Abstract
In this paper, we consider a variant of the classical uncapacitated facility location problem, so-called squared metric two-stage stochastic facility location problem (SM-2-SFLP) which can treat the uncertainty of the set of clients and facility costs. We assume that the connection cost is squared metric, a variant of the metric case which is widely researched. We give a new 0–1 integer linear programming for SM-2-SFLP. Based on the new formulation, we apply two known algorithms to SM-2-SFLP, and analyze the approximation ratio and per-scenario bound respectively.
Similar content being viewed by others
References
Byrka J, Srinivasan A (2018) Approximation algorithms for stochastic and risk-averse optimization. SIAM J Discrete Math 32(1):44–63
Charikar M, Guha S (2005) Improved combinatorial algorithms for facility location problems. SIAM J Comput 34(4):803–824
Chudak FA, Shmoys DB (2003) Improved approximation algorithms for the uncapacitated facility location problem. SIAM J Comput 33(1):1–25
Fernandes CG, Meira LAA, Miyazawa FK, Pedrosa LLC (2015) A systematic approach to bound factor-revealing LPs and its application to the metric and squared metric facility location problems. Math Program 153(2):655–685
Guha S, Khuller S (1999) Greedy strikes back: Improved facility location algorithms. J Algorithms 31(1):228–248
Jain K, Vazirani VV (2001) Approximation algorithms for metric facility location and \(k\)-median problems using the primal-dual schema and Lagrangian relaxation. J ACM 48(2):274–296
Jain K, Mahdian M, Markakis E, Saberi A, Vazirani VV (2003) Greedy facility location algorithms analyzed using dual fitting with factor-revealing LP. J ACM 50(6):795–824
Korupolu MR, Plaxton CG, Rajaraman R (2000) Analysis of a local search heuristic for facility location problems. J Algorithms 37(1):146–188
Li S (2013) A 1.488 approximation algorithm for the uncapacitated facility location problem. Inf Comput 222:45–58
Ravi R, Sinha A (2006) Hedging uncertainty: approximation algorithms for stochastic optimization problems. Math Program 108(1):97–114
Shao J, Xu D (2013) An approximation algorithm for the risk-adjusted two-stage stochastic facility location problem with penalties. J Oper Res Soc China 1(3):339–346
Shmoys DB, Tardos É, Aardal K (1997) Approximation algorithms for facility location problems. In: Proceedings of the 29th annual ACM symposium on theory of computing, pp 265–274
Sviridenko M (2002) An improved approximation algorithm for the metric uncapacitated facility location problem. In: Proceedings of the 9th international conference on integer programming and combinatorial optimization, pp 240–257
Swamy C (2004) Approximation algorithms for clustering problems. Ph.D. thesis. Cornell University
Wu C, Xu D, Shu J (2013) An approximation algorithm for the stochastic fault-tolerant facility location problem. J Oper Res Soc China 1(4):511–522
Wu C, Du D, Xu D (2015) An improved per-scenario bound for the two-stage stochastic facility location problem. Sci China Math 58(1):213–220
Ye Y, Zhang J (2006) An approximation algorithm for the dynamic facility location problem. In: Combinatorial optimization in communication networks. Springer, Boston, MA, pp 623–637
Acknowledgements
The work of the first author is supported by the National Key Research and Development Program of China (Grant No. 2018YFF0213304). The work of the second author is supported by the Higher Educational Science and Technology Program of Shandong Province (Grant No. J17KA171). The work of the third author is supported by the National Natural Science Foundation of China (Grant Nos. 61433012, U1435215). The work of the fourth author is supported by the National Natural Science Foundation of China (Grant No. 11501412). The fifth author is supported by the National Natural Science Foundation of China (Grant Nos. 11531014, 11871081).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, J., Li, M., Wang, Y. et al. Approximation algorithm for squared metric two-stage stochastic facility location problem. J Comb Optim 38, 618–634 (2019). https://doi.org/10.1007/s10878-019-00404-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-019-00404-2
Keywords
Profiles
- Dachuan Xu View author profile