Neighbor sum distinguishing total colorings of IC-planar graphs with maximum degree 13

Abstract

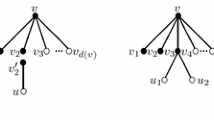
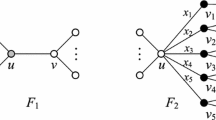
A graph is IC-planar if it admits a drawing on the plane with at most one crossing per edge, such that two pairs of crossing edges share no common end vertex. For a given graph G, a proper total coloring $\phi$ : $V(G)~\cup ~E(G)\rightarrow \{1,2,\ldots ,k\}$ is called neighbor sum distinguishing if $f_{\phi }(u)\ne f_{\phi }(v)$ for each $uv\in E(G)$, where $f_{\phi }(u)$ is the sum of the color of u and the colors of the edges incident with u. The smallest integer k in such a coloring of G is the neighbor sum distinguishing total chromatic number, denoted by $\chi ''_{\Sigma }(G)$. Pilśniak and Woźniak conjectured $\chi _{\Sigma }''(G)\le \Delta (G)+3$ for any simple graph with maximum degree $\Delta (G)$. This conjecture was confirmed for IC-planar graph with maximum degree at least 14. In this paper, by using the discharging method, we prove that this conjecture holds for any IC-planar graph G with $\Delta (G)=13$.