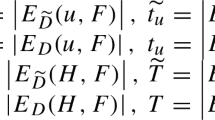Abstract
An edge-colored graph G is a graph with an edge coloring. We say G is properly colored if any two adjacent edges of G have distinct colors, and G is rainbow if any two edges of G have distinct colors. For a vertex \(v \in V(G)\), the color degree \(d_G^{col}(v)\) of v is the number of distinct colors appearing on edges incident with v. The minimum color degree \(\delta ^{col}(G)\) of G is the minimum \(d_G^{col}(v)\) over all vertices \(v \in V(G)\). In this paper, we study the relation between the order of maximum properly colored tree in G and the minimum color degree \(\delta ^{col}(G)\) of G. We obtain that for an edge-colored connected graph G, the order of maximum properly colored tree is at least \(\min \{|G|, 2\delta ^{col}(G)\}\), which generalizes the result of Cheng et al. [Properly colored spanning trees in edge-colored graphs, Discrete Math., 343 (1), 2020]. Moreover, the lower bound \(2\delta ^{col}(G)\) in our result is sharp and we characterize all extremal graphs G with the maximum properly colored tree of order \(2\delta ^{col}(G) \ne |G|\).

Similar content being viewed by others
References
Akbari S, Alipour A (2006) Multicolored trees in complete graphs. J Graph Theory 54:221–232
Alon N, Gutin G (1997) Properly colored Hamilton cycles in edge-colored complete graphs. Random Struct Algorithms 11:179–186
Bang-Jensen J, Gutin G, Yeo A (1998) Properly coloured Hamiltonian paths in edge-coloured complete graphs. Discrete Appl Math 82:247–250
Bollobás B, Erdős P (1976) Alternating Hamiltonian cycles. Israel J Math 23:126–131
Borozan V, Fernandez de La Vega W, Manoussakis Y, Martinhon C, Muthu R, Pham HP, Saad R (2019) Maximum colored trees in edge-colored graphs. Euro J Combin 80:296–310
Brualdi RA, Hollingsworth S (1996) Multicolored trees in complete graphs. J Combin Theory Ser B 68:310–313
Cheng Y, Kano M, Wang G (2020) Properly colored spanning trees in edge-colored graphs. Discrete Math 343(1):111629
Cheng Y, Sun Q, Tan TS, Wang G (2019) Rainbow Hamiltonian cycles in strongly edge-colored graphs. Discrete Math 342(4):1186–1190
Dirac GA (1952) Some theorems on abstract graphs. Proc London Math Soc 2(1):69–81
Feng J, Giesen H, Guo Y, Gutin G, Jensen T, Rafiey A (2006) Characterization of edge-colored complete graphs with properly colored Hamilton paths. J Graph Theory 53:333–346
Fujita S, Magnant C (2011) Properly colored paths and cycles. Discrete Appl Math 159:1391–1397
Horn P (2018) Rainbow spanning trees in complete graphs colored by one-factorizations. J Graph Theory 87:333–346
Kano M, Li X (2008) Monochromatic and heterochromatic subgraphs in edge-colored graphs—a survey. Graphs Combin 24:237–263
Kano M, Ozeki K, Suzuki K, Tsugaki M, Yamashita T (2015) Spanning \(k\)-trees of bipartite graphs. Electron J Combin 22(1):P1.13
Li H (2013) Rainbow \(C^{\prime }_3\)s and \(C^{\prime }_4\)s in edge-colored graphs. Discrete Math 313:1893–1896
Li R, Ning B, Zhang S (2016) Color degree sum conditions for rainbow triangles in edge-colored graphs. Graphs Combin 32:2001–2008
Li H, Wang G (2012) Color degree and heterochromatic cycles in edge-colored graphs. Euro J Combin 33(8):1958–1964
Lo A (2014) A Dirac type condition for properly coloured paths and cycles. J Graph Theory 76:60–87
Lo A (2016) Properly colored Hamiltonian cycles in edge-colored complete graphs. Combinatorica 36(4):471–492
Lo A (2018) Long properly coloured cycles in edge-coloured graphs. J Graph Theory. https://doi.org/10.1002/jgt.22405
Ore O (1960) Note on Hamilton circuits. Am Math Monthly 67:55
Suzuki K (2006) A necessary and sufficient condition for the existence of a heterochromatic spanning tree in a graph. Graphs Combin 22:261–269
Wang G, Li H (2009) Color degree and alternating cycles in edge-colored graphs. Discrete Math 309:4349–4354
Wang G (2011) Rainbow matchings in properly edge colored graphs. Electron J Combin 18:P162
Acknowledgements
The first author is supported by the China Scholarship Council (No. 201806220051). The third author is supported by Grant for Overseas Challenge Program for Young Researchers from JSPS (No. 201980222) and JSPS KAKENHI (No. JP20J15332).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Hu, J., Li, H. & Maezawa, Si. Maximum properly colored trees in edge-colored graphs. J Comb Optim 44, 154–171 (2022). https://doi.org/10.1007/s10878-021-00824-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-021-00824-z