Skip to main content

Advertisement

Springer Nature Link
Log in

Single machine scheduling with non-availability interval and optional job rejection

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

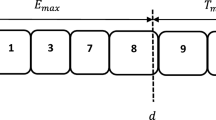
Abstract

This paper studies the single machine scheduling problem with availability constraints and optional job rejection. We consider the non-resumable and resumable variants, and show that the problems remain ordinary NP-hard, even with the rejection possibility extension, by presenting pseudo-polynomial dynamic-programming (DP) solutions. We also present an enhanced running time implementation of the algorithm of Kellerer and Strusevich (Algorithmica 57(4):769–795, 2010) for the resumable scenario without job rejection. This solution is adapted to efficiently solve the machine non-availability problem with a floating interval and the problem of two competing agents on a single machine, with and without optional job rejection. Numerical experiments support the efficiency of our DP implementation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data Availability Statement

The authors declare that the manuscript has no associated data.

References

  • Adiri I, Bruno JL, Frostig E, Kan AHGR (1989) Single machine flow-time scheduling with a single breakdown. Acta Inf 26(7):679–696. https://doi.org/10.1007/BF00288977

    Article  MathSciNet  MATH  Google Scholar 

  • Agnetis A, Mirchandani PB, Pacciarelli D, Pacifici A (2004) Scheduling problems with two competing agents. Oper Res 52(2):229–242

    Article  MathSciNet  Google Scholar 

  • Alhadi G, Kacem I, Laroche P, Osman IM (2018) Maximum lateness minimization on two-parallel machine with a non-availability interval. In: 2018 5th international conference on control decision and information technologies (CoDIT), IEEE, pp 757–762

  • Fiszman S, Mosheiov G (2018) Minimizing total load on a proportionate flowshop with position-dependent processing times and job-rejection. Inf Process Lett 132:39–43

    Article  MathSciNet  Google Scholar 

  • Gerstl E, Mosheiov G (2020) The single machine con problem with unavailability period. Int J Prod Res 59:1–15

    MATH  Google Scholar 

  • Huang W, Wu CC, Liu S (2018) Single-machine batch scheduling problem with job rejection and resource dependent processing times. RAIRO-Oper Res 52(2):315–334

    Article  MathSciNet  Google Scholar 

  • Iranpoor M, Fatemi Ghomi SMT (2019) Integrated due date setting and scheduling on a single machine considering an unexpected unavailability. J Optim Ind Eng 12(1):1–13

    Google Scholar 

  • Kacem I, Chu C (2008) Worst-case analysis of the WSPT and MWSPT rules for single machine scheduling with one planned setup period. Eur J Oper Res 187(3):1080–1089

    Article  MathSciNet  Google Scholar 

  • Kacem I, Kellerer H (2018) Improved fully polynomial approximation schemes for the maximum lateness minimization on a single machine with a fixed operator or machine non-availability interval. In: International conference on computational logistics. Springer, pp 417–427

  • Kellerer H, Strusevich VA (2010) Fully polynomial approximation schemes for a symmetric quadratic knapsack problem and its scheduling applications. Algorithmica 57(4):769–795

    Article  MathSciNet  Google Scholar 

  • Kellerer H, Strusevich VA (2013) Fast approximation schemes for Boolean programming and scheduling problems related to positive convex half-product. Eur J Oper Res 228(1):24–32

    Article  MathSciNet  Google Scholar 

  • Kellerer H, Strusevich VA (2016) Optimizing the half-product and related quadratic Boolean functions: approximation and scheduling applications. Ann Oper Res 240(1):39–94

    Article  MathSciNet  Google Scholar 

  • Kovalyov MY, Mosheiov G, Šešok D (2019) Comments on proportionate flowshops with general position dependent processing times[Inf. Process. Lett. 111 (2011) 174–177] and minimizing total load on a proportionate flowshop with position-dependent processing times and job-rejection [Inf. Process. Lett. 132 (2018) 39–43]. Inf Process Lett 147:1–2

    Article  Google Scholar 

  • Lee C (1996) Machine scheduling with an availability constraint. J Glob Optim 9(3–4):395–416

    Article  MathSciNet  Google Scholar 

  • Lee C (2004) Machine scheduling with availability constraints. In: Handbook of scheduling—algorithms, models, and performance analysis. Springer. https://doi.org/10.1201/9780203489802.ch22

  • Leung JY (2004) Handbook of scheduling: algorithms, models, and performance analysis. CRC Press, Boca Raton

    Book  Google Scholar 

  • Li SS, Chen RX, Feng Q, Jiao CW (2019) Parallel-machine scheduling with job-dependent cumulative deterioration effect and rejection. J Comb Optim 38(3):957–971

    Article  MathSciNet  Google Scholar 

  • Mor B, Mosheiov G (2012) Heuristics for scheduling problems with an unavailability constraint and position-dependent processing times. Comput Ind Eng 62(4):908–916

    Article  Google Scholar 

  • Mor B, Shapira D (2019) Improved algorithms for scheduling on proportionate flowshop with job-rejection. J Oper Res Soc 70(11):1997–2003

    Article  Google Scholar 

  • Mor B, Shapira D (2019) Scheduling with regular performance measures and optional job rejection on a single machine. J Oper Res Soc 71:1–11

    Google Scholar 

  • Mor B, Mosheiov G, Shapira D (2019) Flowshop scheduling with learning effect and job rejection. J Sched 23:1–11

    MathSciNet  MATH  Google Scholar 

  • Mor B, Mosheiov G, Shapira D (2021) Single machine lot scheduling with optional job-rejection. J Comb Optim 41:1–11

    Article  MathSciNet  Google Scholar 

  • Mosheiov G, Sarig A, Strusevich V (2019) Minmax scheduling and due-window assignment with position-dependent processing times and job rejection. 4OR 18:1–18

    MathSciNet  MATH  Google Scholar 

  • Shabtay D, Zofi M (2018) Single machine scheduling with controllable processing times and an unavailability period to minimize the makespan. Int J Prod Econ 198:191–200

    Article  Google Scholar 

  • Shabtay D, Gaspar N, Kaspi M (2013) A survey on offline scheduling with rejection. J Sched 16(1):3–28

    Article  MathSciNet  Google Scholar 

  • Strusevich V, Rustogi K (2017) Scheduling with time-changing effects and rate-modifying activities. Springer, Berlin

    Book  Google Scholar 

  • Wan L, Yuan J (2018) Single-machine scheduling with operator non-availability to minimize total weighted completion time. Inf Sci 445:1–5

    Article  MathSciNet  Google Scholar 

  • Wang D, Yin Y, Cheng T (2018) Parallel-machine rescheduling with job unavailability and rejection. Omega 81:246–260

    Article  Google Scholar 

  • Wang G, Sun H, Chu C (2005) Preemptive scheduling with availability constraints to minimize total weighted completion times. Ann Oper Res 133:183–192

    Article  MathSciNet  Google Scholar 

  • Zuo L, Sun Z, Lu L, Zhang L (2019) Single-machine scheduling with rejection and an operator non-availability interval. Mathematics 7(8):668

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Economics and Business Administration, Ariel University, Ariel, Israel

    Baruch Mor

  2. Department of Computer Science, Ariel University, Ariel, Israel

    Dana Shapira

Authors
  1. Baruch Mor
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dana Shapira
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dana Shapira.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mor, B., Shapira, D. Single machine scheduling with non-availability interval and optional job rejection. J Comb Optim 44, 480–497 (2022). https://doi.org/10.1007/s10878-022-00845-2

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-022-00845-2

Keywords

Profiles

  1. Baruch Mor View author profile