Minimizing total weighted late work on a single-machine with non-availability intervals

Abstract

We explore the problem of scheduling n jobs on a single machine in which there are m fixed machine non-availability intervals. The target is to seek out a feasible solution that minimizes total weighted late work. Three variants of the problem are investigated. The first is the preemptive version, the second is the resumable version, and the third is the non-resumable version. For the first one, we present an $O((m+n) \log n)$-time algorithm to solve it. For the second one, we develop an exact dynamic programming algorithm and a fully polynomial time approximation scheme. For the third one, we first demonstrate that it is strongly $\mathcal{NP}\mathcal{}$-hard for the case where all jobs have the unit weight and common due date, and then we develop a pseudo-polynomial time algorithm for the unit weight case where the number of non-availability intervals is fixed, finally we propose a pseudo-polynomial time algorithm for the case where there is only one non-availability interval.

Appendix

Consider an instance of $1 | h(1), n-res| \sum w_j Y_j$ in which it contains six jobs and one MNAI ${\mathcal {I}} = [7, 9]$, where job parameters is given in Table 3.

Table 3 The job data of the instance

By Eq. (17), the set of possible candidate jobs in $\mathcal {{\mathcal {S}}}_2^N$ is ${\mathcal {M}}=\{J_4, J_5, J_6, J_7\}$. We illustrate the execution of Algorithm 6 by choosing $J_4$ as the candidate job in ${\mathcal {S}}_2^N$ having the smallest index and solve ${\mathcal {P}}_4$ as follows:

Step 1. Set ${\mathcal {Q}}_0(4)=\{(0, 0, 0, 0)\}$ and ${{\mathcal {Q}}}_j(4)=\emptyset$ for $j=1, 2, \ldots , 6$.

Step 2. For $j=1<4$, $J_1$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_1(4)=\{(0, 0, 0, 2), (0, 2, 0, 0), (1, 0, 0, 0)\}$, see Table 4 for the creation procedure.

Table 4 Creation of ${\mathcal {Q}}_1(4)$ from ${\mathcal {Q}}_0(4)$

For $j=2<4$, $J_2$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_2(4)=\{(0, 0, 0, 8), (2, 0, 0, 2), (0, 3, 0, 2), (1, 0, 0, 6), (0, 2, 0, 6), (2, 2, 0, 0), (0, 5, 0, 2)\}$, see Table 5 for the creation procedure.

Table 5 Creation of ${\mathcal {Q}}_2(4)$ from ${\mathcal {Q}}_1(4)$

For $j\!=\!3\!<\!4$, $J_3$ falls into Case 1. Algorithm 6 executes Step 2.2, we obtain ${\mathcal {Q}}_3(4)=\{(0, 0, 0, 20), (0, 2, 0, 18), (0, 3, 0, 14), (0, 4, 0, 8), (0, 5, 0, 14), (0, 6, 0, 6), (0, 7, 0, 5), (1, 0, 0, 18), (2, 0, 0, 14), (2, 2, 0, 12), (3, 0, 0, 8), (3, 2, 0, 6)\}$, see Table 6 for the creation procedure.

Table 6 Creation of ${\mathcal {Q}}_3(4)$ from ${\mathcal {Q}}_2(4)$

For $j=4$, $J_4$ falls into Case 2. Algorithm 6 executes Step 2.3, we obtain ${\mathcal {Q}}_4(4)=\{(0, 0, 3, 20), (0, 2, 3, 18), (0, 3, 3, 14), (0, 4, 3, 8), (0, 5, 3, 14), (0, 6, 3, 6), (0, 7, 3, 5), (4, 0, 0, 20), (4, 2, 0, 18), (4, 3, 0, 14), (4, 4, 0, 8), (4, 5, 0, 14), (4, 6, 0, 6), (4, 7, 0, 5)\}$, see Table 7 for the creation procedure.

Table 7 Creation of ${\mathcal {Q}}_4(4)$ from ${\mathcal {Q}}_3(4)$

For $j=5>4$, $J_5$ falls into Case 3. Algorithm 6 executes Step 2.4 and Step 2.5, we obtain ${\mathcal {Q}}_5(4)=\{(0, 0, 3, 32), (0, 0, 7, 26), (0, 2, 3, 30), (0, 2, 7, 24), (0, 3, 3, 26), (0, 3, 7, 20), (0, 4, 3, 20)$, $(0, 4, 7, 14), (0, 5, 3, 26), (0, 5, 7, 20), (0, 6, 3, 18), (0, 6, 7, 12), (0, 7, 3, 14), (0, 7, 7, 11), (4, 0, 0, 32)$, $(4, 2, 0, 30), (4, 3, 0, 26), (4, 4, 0, 20), (4, 5, 0, 26), (4, 6, 0, 18), (4, 7, 0, 14), (5, 0, 3, 20), (5, 2, 3, 18)$, $(5, 3, 3, 14), (5, 4, 3, 8), (5, 5, 3, 14), (5, 6, 3, 6), (5, 7, 3, 5)\}$, see Table 8 for the creation procedure, where the underlined state $(k, t_1, t_2, l)^{x}$ is dominated by the corresponding state ${(r, t_1, t_2, l)}^{(x)}$.

Table 8 Creation of ${\mathcal {Q}}_5(4)$ from ${\mathcal {Q}}_4(4)$

For $j=6>4$, $J_6$ falls into Case 3. Algorithm 6 executes Step 2.4 and Step 2.5, we obtain ${\mathcal {Q}}_6(4)=\{(0, 0, 3, 44), (0, 0, 5, 32), (0, 0, 7, 38), (0, 2, 3, 32), (0, 2, 5, 30), (0, 2, 7, 26), (0, 3, 3, 38)$, $(0, 3, 5, 26), (0, 3, 7, 32), (0, 4, 3, 30), (0, 4, 5, 20), (0, 4, 7, 24), (0, 5, 3, 26), (0, 5, 7, 20), (0, 5, 5, 26)$, $(0, 6, 3, 20), (0, 6, 5, 18), (0, 6, 7, 14), (0, 7, 3, 26), (0, 7, 5, 14), (0, 7, 7, 20) \}$, see Table 9 for the creation procedure, where those state $(r, t_1, t_2, l) \in {\mathcal {Q}}_6(4)$ with $r > 0$ are deleted (by Remark 4.8).

Table 9 Creation of ${\mathcal {Q}}_6(4)$ from ${\mathcal {Q}}_5(4)$

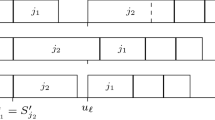
Step 3. $V_{nr}^{*}(4)=\min \{l: (0, t_1, t_2, l)\} \in {\mathcal {Q}}_6(4)\}=14$, the states (0, 6, 7, 14) and (0, 7, 5, 14) both correspond to the optimal value 14 for ${\mathcal {P}}_4$, see Figs. 2 and 3 for their corresponding optimal schedules, where the late jobs in ${\mathcal {S}}_2^L$ are omitted.

Fig. 2

The schedule corresponding to the state (0, 6, 7, 14) of ${\mathcal {P}}_4$

Fig. 3

The schedule corresponding to the state (0, 7, 5, 14) of ${\mathcal {P}}_4$