On metric dimension of plane graphs with $\frac{m}{2}$ number of 10 sided faces

Abstract

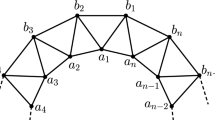
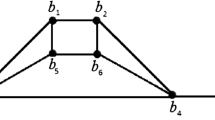
Let $\Gamma =\Gamma (V, E)$ be a simple (multiple edges and loops are not considered), connected (every pair of distinct vertices are joined by a path), and an undirected (all edges are bidirectional) graph, with the vertex set V and the edge set E. The length of the shortest path (geodesic distance) between two vertices p and q, denoted by d(p, q), is the minimum number of edges lying between the vertices p and q. The resolvability parameters for graph $\Gamma$ are a relatively new advanced area in which the complete network is built so that each vertex or/and edge signifies a unique position. The challenge of characterizing families of planar graphs with constant and bounded metric dimensions is a widely studied topic. In this paper, we consider three new families of planar graphs viz., $A_m$, $B_m$, and $C_m$ (where $m\ge 6$ is always even natural), and study their metric dimensions. We prove that only 3 non-adjacent vertices are sufficient to resolve every pair of distinct vertices of $A_m$, $B_m$, and $C_m$.