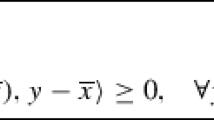Abstract
We prove that under suitable conditions, the solution set of a variational inequality, governed by perturbed monotone operators depending on a parameter, has a continuous selection. In the nonparametric case this can be considered as a variational principle for variational inequalities, an analogue of the Borwein–Preiss variational principle. An applications of this result is given.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Aubin, J.-P., Ekeland, I.: Applied Nonlinear Analysis. John Wiley & Sons (1984)
Borwein J.M., Preiss D.: A smooth variational principle with applications to subdifferentiability and to differentiability of convex functions. Trans. Amer. Math. Soc. 303, 517–527 (1987)
Borwein J.M., Zhu Q.J.: Viscosity solutions and viscosity subderivatives in smooth Banach spaces with applications to metric regularity SIAM J. Control Optim. 34(5), 1568–1591 (1996)
Deville R., Godefroy G., Zizler V.: Smoothness and Renormings in Banach Spaces, Pitman Monographs No. 64. Longman, London (1993)
Georgiev P.G.: Parametric Ekeland’s variational principle. Appl. Math. Lett. 14(6), 691–696 (2001)
Georgiev P.G.: Parametric Borwein–Preiss variational principle and applications. Proc. Amer. Math. Soc. 133(11), 3211–3225 (2005)
Kinderlehrer D., Stampacchia G.: An introduction to variational inequalities and their applications. Pure and Applied Mathematics 88. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers, New York (1980)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Georgiev, P.G. Parameterized variational inequalities. J Glob Optim 47, 457–462 (2010). https://doi.org/10.1007/s10898-009-9424-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10898-009-9424-0