Approximations for two variants of the Steiner tree problem in the Euclidean plane ${\mathbb{R}^2}$

Abstract

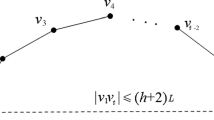
Given n terminals in the Euclidean plane and a positive constant l, find a Steiner tree T interconnecting all terminals with the minimum total cost of Steiner points and a specific material used to construct all edges in T such that the Euclidean length of each edge in T is no more than l. In this paper, according to the cost b of each Steiner point and the different costs of some specific materials with the different lengths, we study two variants of the Steiner tree problem in the Euclidean plane as follows: (1) If a specific material to construct all edges in such a Steiner tree has its infinite length and the cost of per unit length of such a specific material used is c ₁, the objective is to minimize the total cost of the Steiner points and such a specific material used to construct all edges in T, i.e., ${{\rm min} \{b \cdot k_1+ c_1 \cdot \sum_{e \in T} w(e)\}}$, where T is a Steiner tree constructed, k ₁ is the number of Steiner points and w(e) is the length of part cut from such a specific material to construct edge e in T, and we call this version as the minimum-cost Steiner points and edges problem (MCSPE, for short). (2) If a specific material to construct all edges in such a Steiner tree has its finite length L (l ≤ L) and the cost of per piece of such a specific material used is c ₂, the objective is to minimize the total cost of the Steiner points and the pieces of such a specific material used to construct all edges in T, i.e., ${{\rm min} \{b \cdot k_2+ c_2 \cdot k_3\}}$, where T is a Steiner tree constructed, k ₂ is the number of Steiner points in T and k ₃ is the number of pieces of such a specific material used, and we call this version as the minimum-cost Steiner points and pieces of specific material problem (MCSPPSM, for short). These two variants of the Steiner tree problem are NP-hard with some applications in VLSI design, WDM optical networks and wireless communications. In this paper, we first design an approximation algorithm with performance ratio 3 for the MCSPE problem, and then present two approximation algorithms with performance ratios 4 and 3.236 for the MCSPPSM problem, respectively.