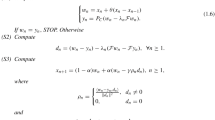Skip to main content

Advertisement

Springer Nature Link
Log in

Inertial projection and contraction algorithms with larger step sizes for solving quasimonotone variational inequalities

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

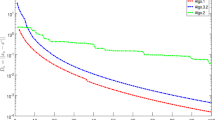
This paper deals with a class of inertial projection and contraction algorithms for solving a variational inequality problem involving quasimonotone and Lipschitz continuous mappings in Hilbert spaces. The algorithms incorporate inertial techniques and the Barzilai–Borwein step size strategy, moreover their line search conditions and some parameters are relaxed to obtain larger step sizes. The weak convergence of the algorithms is proved without the knowledge of the Lipschitz constant of the mappings. Meanwhile, the nonasymptotic convergence and the linear convergence of the algorithms are established. Some numerical experiments show that the proposed algorithms are more effective than some existing ones.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Facchinei, F., Pang, J.S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer, Berlin (2003)

    MATH  Google Scholar 

  2. Kinderlehrer, D., Stampacchia, G.: An Introduction to Variational Inequalities and Their Applications. Academic Press, New York (1980)

    MATH  Google Scholar 

  3. Konnov, I.V.: Combined Relaxation Methods for Variational Inequalities. Springer, Berlin (2000)

    MATH  Google Scholar 

  4. Konnov, I.V.: Equilibrium Models and Variational Inequalities. Elsevier, Amsterdam (2007)

    MATH  Google Scholar 

  5. Wang, Z.B., Chen, Z.Y., Xiao, X.B., Zhang, C.: A new projection-type method for solving multi-valued mixed variational inequalities without monotonicity. Appl. Anal. 99(9), 1453–1466 (2020)

    Article  MathSciNet  Google Scholar 

  6. Abubakar, J., Kumam, P., ur Rehman, H.: Self-adaptive inertial subgradient extragradient scheme for solving pseudomontone variational inequality problem. Int. J. Nonlinear Sci. Numer. Simul. (2021). https://doi.org/10.1515/ijnsns-2020-0033

  7. Abubakar, J., Kumam, P., ur Rehman, H., Hassan-Ibrahim, A.: Inertial iterative schemes with variable step sizes for variational inequality problem involving pseudomonotone operator. Mathematics 8, 609 (2020)

    Article  Google Scholar 

  8. He, B.S.: A class of projection and contraction methods for monotone variational inequalities. Appl. Math. Optim. 35, 69–76 (1997)

    Article  MathSciNet  Google Scholar 

  9. He, B.S., Liao, L.Z.: Improvements of some projection methods for monotone nonlinear variational inequalities. J. Optim. Theory Appl. 112, 111–128 (2002)

    Article  MathSciNet  Google Scholar 

  10. Cai, X., Gu, G., He, B.: On the \(O(1/t)\) convergence rate of the projection and contraction methods for variational inequalities with Lipschitz continuous monotone operators. Comput. Optim. Appl. 57(2), 339–363 (2014)

    Article  MathSciNet  Google Scholar 

  11. Barzilai, J., Borwein, J.W.: Two-point step size gradient methods. IMA J. Numer. Anal. 8, 141–148 (1988)

    Article  MathSciNet  Google Scholar 

  12. Liu, W., Dai, Y.H.: Minimization algorithms based on supervisor and searcher cooperation. J. Optim. Theory Appl. 111, 359–379 (2001)

    Article  MathSciNet  Google Scholar 

  13. Dai, Y.H., Fletcher, R.: Projected Barzilai–Borwein methods for large-scale box constrained quadratic programming. Numer. Math. 100, 21–47 (2005)

    Article  MathSciNet  Google Scholar 

  14. Dai, Y.H., Fletcher, R.: New algorithms for singly linearly constrained quadratic programs subject to lower and upper bounds. Math. Program. 106, 403–421 (2006)

    Article  MathSciNet  Google Scholar 

  15. He, H.J., Han, D.R., Li, Z.B.: Some projection methods with the BB step sizes for variational inequalities. J. Comput. Appl. Math. 236, 2590–2604 (2012)

    Article  MathSciNet  Google Scholar 

  16. Dong, X., Cai, X., Han, D.: Prediction–correction method with BB step sizes. Front. Math. China 13, 1325–1340 (2018)

    Article  MathSciNet  Google Scholar 

  17. Qu, Y., Tong, W., He, H., Liou, Y.C.: On projected alternating BB methods for variational inequalities. Optimization (2020). https://doi.org/10.1080/02331934.2020.1721495

    Article  MATH  Google Scholar 

  18. Ye, M.L., He, Y.R.: A double projection method for solving variational inequalities without monotonicity. Comput. Optim. Appl. 60, 141–150 (2015)

    Article  MathSciNet  Google Scholar 

  19. He, X., Huang, N.J., Li, X.S.: Modified projection methods for solving multi-valued variational inequality without monotonicity. Netw. Spat. Econ. (2019). https://doi.org/10.1007/s11067-019-09485-2

    Article  Google Scholar 

  20. Liu, H., Yang, J.: Weak convergence of iterative methods for solving quasimonotone variational inequalities. Comput. Optim. Appl. 77, 491–508 (2020)

    Article  MathSciNet  Google Scholar 

  21. Attouch, H., Goudon, X., Redont, P.: The heavy ball with friction. I. The continuous dynamical system. Commun. Contemp. Math. 2, 1–34 (2000)

    Article  MathSciNet  Google Scholar 

  22. Attouch, H., Czarnecki, M.O.: Asymptotic control and stabilization of nonlinear oscillators with nonisolated equilibria. J. Differ. Equ. 179, 278–310 (2002)

    Article  Google Scholar 

  23. Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for non-convex optimization. SIAM J. Imaging Sci. 7, 1388–1419 (2014)

    Article  MathSciNet  Google Scholar 

  24. Shehu, Y., Iyiola, O.S., Li, X.H., et al.: Convergence analysis of projection method for variational inequalities. Comput. Appl. Math. 38, 161 (2019)

    Article  MathSciNet  Google Scholar 

  25. Thong, D.V., Vinh, N.T., Cho, Y.J.: New strong convergence theorem of the inertial projection and contraction method for variational inequality problems. Numer. Algorithms 84, 285–305 (2020)

    Article  MathSciNet  Google Scholar 

  26. Dong, Q.L., Cho, Y.J., Zhong, L.L., Rassias, ThM: Inertial projection and contraction algorithms for variational inequalities. J. Glob. Optim. 70(3), 687–704 (2018)

    Article  MathSciNet  Google Scholar 

  27. Shehu, Y., Iyiola, O.S.: Projection methods with alternating inertial steps for variational inequalities: weak and linear convergence. Appl. Numer. Math. 157, 315–337 (2020)

    Article  MathSciNet  Google Scholar 

  28. Cholamjiak, P., Thong, D.V., Cho, Y.J.: A novel inertial projection and contraction method for solving pseudomonotone variational inequality problems. Acta. Appl. Math. 169, 217–245 (2020)

    Article  MathSciNet  Google Scholar 

  29. Hieu, D.V., Cho, Y.J., Xiao, Y.B.: Modified accelerated algorithms for solving variational inequalities. J. Comput. Math. 97(11), 2233–2258 (2020)

    MathSciNet  MATH  Google Scholar 

  30. Hieu, D.V., Strodiot, J.J., Muu, L.D.: An explicit extragradient algorithm for solving variational inequalities. J. Optim. Theory Appl. 185, 476–503 (2020)

    Article  MathSciNet  Google Scholar 

  31. Yang, J., Liu, H.: A self-adaptive method for pseudomonotone equilibrium problems and variational inequalities. Comput. Optim. Appl. 75, 423–440 (2020)

    Article  MathSciNet  Google Scholar 

  32. Thong, D.V., Hieu, D.V., Rassias, T.M.: Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems. Optim. Lett. 14(1), 115–144 (2020)

    Article  MathSciNet  Google Scholar 

  33. Tang, G.J., Huang, N.J.: Existence theorems of the variational–hemivariational inequalities. J. Glob. Optim. 56, 605–622 (2013)

    Article  MathSciNet  Google Scholar 

  34. Goebel, K., Reich, S.: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings. Marcel Dekker, New York (1984)

    MATH  Google Scholar 

  35. Zarantonello, E.H.: Projections on convex sets in Hilbert space and spectral theory. In: Zarantonello, E.H. (ed.) Contributions to Nonlinear Functional Analysis. Academic Press, New York (1971)

    MATH  Google Scholar 

  36. Mashreghi, J., Nasri, M.: Forcing strong convergence of Korpelevichs method in Banach spaces with its applications in game theory. Nonlinear Anal. 72, 2086–2099 (2010)

    Article  MathSciNet  Google Scholar 

  37. Hadjisavvas, N., Schaible, S.: Quasimonotone variational inequalities in Banach spaces. J. Optim. Theory Appl. 90(1), 95–111 (1996)

    Article  MathSciNet  Google Scholar 

  38. Alvarez, F.: Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert spaces. SIAM J. Optim. 14, 773–782 (2004)

    Article  MathSciNet  Google Scholar 

  39. Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, Berlin (2011)

    Book  Google Scholar 

  40. Kim, D.S., Vuong, P.T., Khanh, P.D.: Qualitative properties of strongly pseudomonotone variational inequalities. Optim. Lett. 10, 1669–1679 (2016)

    Article  MathSciNet  Google Scholar 

  41. Hieu, D.V., Cho, Y.J., Xiao, Y.B., Kumam, P.: Relaxed extragradient algorithm for solving pseudomonotone variational inequalities in Hilbert spaces. Optimization 69(10), 2279–2304 (2020)

    Article  MathSciNet  Google Scholar 

  42. Aujol, J.F., Dossal, C., Rondepierre, A.: Optimal convergence rates for Nesterov acceleration. SIAM J. Optim. 29(4), 3131–3153 (2019)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The important part of the paper was done when the first author was a visitor at Department of Statistics & Applied Probability, National University of Singapore. The first author is profoundly grateful to professor Yu Tao, for his help and encouragement. The authors are indebted to the anonymous Editor and referees for their valuable comments and suggestions which helped us very much in improving the original version of this paper. This work was supported by the National Natural Science Foundation of China (11701479, 11701478), the Chinese Postdoctoral Science Foundation (2018M643434) and the Fundamental Research Funds for the Central Universities (A0920502052101-335).

Author information

Authors and Affiliations

  1. Department of Mathematics, Southwest Jiaotong University, Chengdu, 611756, Sichuan, China

    Zhong-bao Wang, Jiang Yi & Zhang-you Chen

  2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu, 611756, Sichuan, China

    Zhong-bao Wang, Jiang Yi & Zhang-you Chen

  3. School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, 611731, Sichuan, China

    Zhong-bao Wang

  4. School of Economics and Management, Southwest Jiaotong University, Chengdu, 610031, Sichuan, China

    Xue Chen

Authors
  1. Zhong-bao Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xue Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jiang Yi
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Zhang-you Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Zhong-bao Wang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Zb., Chen, X., Yi, J. et al. Inertial projection and contraction algorithms with larger step sizes for solving quasimonotone variational inequalities. J Glob Optim 82, 499–522 (2022). https://doi.org/10.1007/s10898-021-01083-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-021-01083-2

Keywords