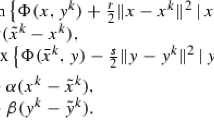Skip to main content
Springer Nature Link
Log in

Solving saddle point problems: a landscape of primal-dual algorithm with larger stepsizes

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We consider a class of saddle point problems frequently arising in the areas of image processing and machine learning. In this paper, we propose a simple primal-dual algorithm, which embeds a general proximal term induced with a positive definite matrix into one subproblem. It is remarkable that our algorithm enjoys larger stepsizes than many existing state-of-the-art primal-dual-like algorithms due to our relaxed convergence-guaranteeing condition. Moreover, our algorithm includes the well-known primal-dual hybrid gradient method as its special case, while it is also of possible benefit to deriving partially linearized primal-dual algorithms. Finally, we show that our algorithm is able to deal with multi-block separable saddle point problems. In particular, an application to a multi-block separable minimization problem with linear constraints yields a parallel algorithm. Some computational results sufficiently support the promising improvement brought by our relaxed requirement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Arrow, K., Hurwicz, L., Uzawa, H.: With contributions. In: Chenery, H.B., Johnson, S.M., Karlin, S., Marschak, T., Solow, R.M. (eds.) Studies in Linear and Non-Linear Programming, Stanford Mathematical Studies in the Social Science, vol. II. Stanford Unversity Press, Stanford, California (1958)

  2. Bonettini, S., Ruggiero, V.: On the convergence of primal-dual hybrid gradient algorithms for total variation image restoration. J. Math. Imaging Vis. 44, 236–253 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  3. Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3, 1–122 (2010)

    Article  MATH  Google Scholar 

  4. Cai, X., Han, D., Xu, L.: An improved first-order primal-dual algorithm with a new correction step. J. Global Optim. 57, 1419–1428 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  5. Candés, E., Li, X., Ma, Y., Wright, J.: Robust principal component analysis? J. ACM 58, 1–37 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  6. Candés, E., Romberg, J., Tao, T.: Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59, 1207–1223 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. J. Math. Imaging Vis. 40, 120–145 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chambolle, A., Pock, T.: An introduction to continuous optimization for imaging. Acta Numer. 25, 161–319 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  9. Chang, X., Yang, J.: A golden ratio primal-dual algorithm for structured convex optimization. J. Sci. Comput. 87(2), 47 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chen, P., Huang, J., Zhang, X.: A primal-dual fixed point algorithm for convex separable minimization with applications to image restoration. Inverse Probl. 29(2), 025011 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  11. Donoho, D.: Compressed sensing. IEEE Trans. Inform. Theory 52, 1289–1306 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  12. Dontchev, A.L., Rockafellar, R.T.: Regularity and conditioning of solution mappings in variational analysis. Set-Valued Anal. 12(1), 79–109 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Dontchev, A.L., Rockafellar, R.T.: Implicit Functions and Solution Mappings. Springer Monographs in Mathematics, vol. 208. Springer, Berlin (2009)

    Book  MATH  Google Scholar 

  14. Drori, Y., Sabach, S., Teboulle, M.: A simple algorithm for a class of nonsmooth convex-concave saddle-point problems. Oper. Res. Lett. 43(2), 209–214 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Esser, E., Zhang, X., Chan, T.: A general framework for a class of first-order primal-dual algorithms for convex optimization in imaging sciences. SIAM J. Imaging Sci. 3, 1015–1046 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  16. He, B., Ma, F., Xu, S., Yuan, X.: A generalized primal-dual algorithm with improved convergence condition for saddle point problems (2021). arXiv:2112.00254v1

  17. He, B., Yuan, X.: Convergence analysis of primal-dual algorithms for a saddle-point problem: from contraction perspective. SIAM J. Imaging Sci. 5, 119–149 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  18. He, B., Yuan, X.: Balanced augmented Lagrangian method for convex programming (2021). arXiv:2108.08554

  19. He, B., You, Y., Yuan, X.: On the convergence of primal dual hybrid gradient algorithm. SIAM J. Imaging Sci. 7, 2526–2537 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. He, H., Desai, J., Wang, K.: A primal dual prediction correction algorithm for saddle point optimization. J. Global Optim. 66, 573–583 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jiang, F., Wu, Z., Cai, X., Zhang, H.: A first-order inexact primal-dual algorithm for a class of convex-concave saddle point problems. Numer. Algorithms 88, 1109–1136 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  22. Jiang, F., Wu, Z., Cai, X., Zhang, H.: Unified linear convergence of first-order primal-dual algorithms for saddle point problems. Optim. Lett. 16, 1675–1700 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Li, H., Yan, M.: On the improved conditions for some primal-dual algorithms (2022). arXiv:2201.00139v1

  24. Li, Z., Yan, M.: New convergence analysis of a primal-dual algorithm with large stepsizes. Adv. Comput. Math. 47(1), 1–20 (2021)

    Article  MathSciNet  Google Scholar 

  25. Loris, I., Verhoeven, C.: On a generalization of the iterative soft-thresholding algorithm for the case of non-separable penalty. Inverse Probl. 27(12), 125007 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Moreau, J.: Fonctions convexe dudual et points proximaux dans un espace hilbertien. C. R. Acad. Sci. Paris Ser. A Math. 255, 2897–2899 (1962)

    MATH  Google Scholar 

  27. O’Connor, D., Vandenberghe, L.: On the equivalence of the primal-dual hybrid gradient method and Douglas–Rachford splitting. Math. Program. 179(1), 85–108 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1, 123–231 (2013)

    Google Scholar 

  29. Robinson, S.M.: Some continuity properties of polyhedral multifunctions. In: Mathematical Programming at Oberwolfach, pp. 206–214. Springer (1981)

  30. Rudin, L., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D 60, 227–238 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  31. Wang, K., He, H.: A double extrapolation primal-dual algorithm for saddle point problems. J. Sci. Comput. 85(3), 1–30 (2020)

    MathSciNet  MATH  Google Scholar 

  32. Zhu, M., Chan, T.: An Efficient Primal-Dual Hybrid Gradient Algorithm for Total Variation Image Restoration. CAM Reports 08-34, UCLA (2008)

Download references

Acknowledgements

The authors are grateful to two anonymous referees for their valuable comments on this paper; especially for one referee bringing our attention to the relevant reference [23]. This research was partially supported by the National Natural Science Foundation of China (Nos. 11301123, 11771113, 12201309) and the Startup Foundation for Introducing Talent of NUIST (No. 2022r027).

Author information

Authors and Affiliations

  1. Department of Information and Computing Science, School of Mathematics and Statistics, Nanjing University of Information Science and Technology, Nanjing, 210044, China

    Fan Jiang

  2. School of Mathematical Sciences, Xiamen University, Xiamen, 360015, China

    Zhiyuan Zhang

  3. School of Mathematics and Statistics, Ningbo University, Ningbo, 315211, China

    Hongjin He

Authors
  1. Fan Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhiyuan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hongjin He
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hongjin He.

Ethics declarations

Availability of data and material

Not applicable.

Code availability

The Matlab code employed to run the numerical experiments is available upon request to the corresponding author.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, F., Zhang, Z. & He, H. Solving saddle point problems: a landscape of primal-dual algorithm with larger stepsizes. J Glob Optim 85, 821–846 (2023). https://doi.org/10.1007/s10898-022-01233-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-022-01233-0

Keywords