Skip to main content

Advertisement

Springer Nature Link
Log in

The restricted inverse optimal value problem on shortest path under \(l_1\) norm on trees

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

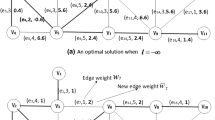
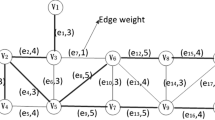
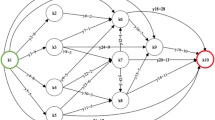
We consider the restricted inverse optimal value problem on shortest path under weighted \(l_1\) norm on trees (RIOVSPT\(\varvec{_1}\)). It aims at adjusting some edge weights to minimize the total cost under weighted \(l_1\) norm on the premise that the length of the shortest root-leaf path of the tree is lower-bounded by a given value D, which is just the restriction on the length of a given root-leaf path \(P_0\). If we ignore the restriction on the path \(P_0\), then we obtain the minimum cost shortest path interdiction problem on trees (MCSPIT\(\varvec{_1}\)). We analyze some properties of the problem (RIOVSPT\(\varvec{_1}\)) and explore the relationship of the optimal solutions between (MCSPIT\(\varvec{_1}\)) and (RIOVSPT\(\varvec{_1}\)). We first take the optimal solution of the problem (MCSPIT\(\varvec{_1}\)) as an initial infeasible solution of problem (RIOVSPT\(\varvec{_1}\)). Then we consider a slack problem \({\textbf {(}} {{\textbf {RIOVSPT}}}\varvec{_1^s)}\), where the length of the path \(P_0\) is greater than D. We obtain its feasible solutions gradually approaching to an optimal solution of the problem (RIOVSPT\(\varvec{_1}\)) by solving a series of subproblems \({{\textbf {(RIOVSPT}}}\varvec{_1^i)}\). It aims at determining the only weight-decreasing edge on the path \(P_0\) with the minimum cost so that the length of the shortest root-leaf path is no less than D. The subproblem can be solved by searching for a minimum cost cut in O(n) time. The iterations continue until the length of the path \(P_0\) equals D. Consequently, the time complexity of the algorithm is \(O(n^2)\) and we present some numerical experiments to show the efficiency of the algorithm. Additionally, we devise a linear time algorithm for the problem (RIOVSPT\(\varvec{_{u1}}\)) under unit \(l_1\) norm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Ahmed, S., Guan, Y.: The inverse optimal value problem. Math. Program. 102(1), 91–110 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  2. Burton, D., Toint, P.L.: On an instance of the inverse shortest paths problem. Math. Program. 53(1–3), 45–61 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  3. Burton, D., Toint, P.L.: On the use of an inverse shortest paths algorithm for recovering linearly correlated costs. Math. Program. 63(1), 1–22 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cui, T., Hochbaum, D.S.: Complexity of some inverse shortest path lengths problems. Networks 56(1), 20–29 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Lv, Y., Hu, T., Wan, Z.: A penalty function method for solving inverse optimal value problem. J. Comput. Appl. Math. 220(1), 175–180 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  6. Paleologo, G., Takriti, S.: Bandwidth trading: a new market looking for help from the OR community. AIRO News VI 3, 1–4 (2001)

    Google Scholar 

  7. Wang, H., Guan, X.C., Zhang, Q., Zhang, B.W.: Capacitated inverse optimal value problem on minimum spanning tree under bottleneck hamming distance. J. Combin. Optim. 41(4), 861–887 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  8. Xu, S., Zhang, J.: An inverse problem of the weighted shortest path problem. Jpn. J. Ind. Appl. Math. 12(1), 47–60 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  9. Zhang, B.W., Wang, Q.: Inverse shortest path problems under Hamming distance. J. Hohai Univ. (Nat. Sci.) 36(4), 571–574 (2008)

    MathSciNet  Google Scholar 

  10. Zhang, B.W., Guan, X.C., Pardalos, P.M., Wang, H., Zhang, Q., Liu, Y., Chen, S.Y.: The lower bounded inverse optimal value problem on minimum spanning tree under unit \(l_{\infty }\) norm. J. Glob. Optim. 79(3), 757–777 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhang, B.W., Guan, X.C., Zhang, Q.: Inverse optimal value problem on minimum spanning tree under unit \(l_{\infty }\) norm. Optim. Lett. 14(8), 2301–2322 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhang, J., Ma, Z., Yang, C.: A column generation method for inverse shortest path problems. Zeitschrift für Oper. Res. 41(3), 347–347 (1995)

    MathSciNet  MATH  Google Scholar 

  13. Zhang, Q., Guan, X.C., Pardalos, P.M.: Maximum shortest path interdiction problem by upgrading edges on trees under weighted \(l_1\) norm. J. Glob. Optim. 79(4), 959–987 (2021)

    Article  MATH  Google Scholar 

  14. Zhang, Q., Guan, X.C., Wang, H., Pardalos, P.M.: Maximum shortest path interdiction problem by upgrading edges on trees under Hamming distance. Optim. Lett. 15(8), 2661–2680 (2021)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, Southeast University, Nanjing, 210096, China

    Qiao Zhang, Xiucui Guan, Junhua Jia & Xinqiang Qian

  2. Center for Applied Optimization, University of Florida, Gainesville, FL, 32611, USA

    Panos M. Pardalos

  3. LATNA, Higher School of Economics, Nizhni Novgorod, Russia

    Panos M. Pardalos

Authors
  1. Qiao Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiucui Guan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Junhua Jia
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Xinqiang Qian
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Panos M. Pardalos
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiucui Guan.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The work of X.C. Guan was supported by National Natural Science Foundation of China (11471073). The work of P.M. Pardalos was conducted within the framework of the Basic Research Program at the National Research University Higher School of Economics (HSE).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Q., Guan, X., Jia, J. et al. The restricted inverse optimal value problem on shortest path under \(l_1\) norm on trees. J Glob Optim 86, 251–284 (2023). https://doi.org/10.1007/s10898-022-01256-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-022-01256-7

Keywords

Profiles

  1. Xiucui Guan View author profile