Skip to main content
Springer Nature Link
Log in

The Use of Curved Elements in the Finite Element Approximation of Thin Plates by High Order p and hp Methods

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

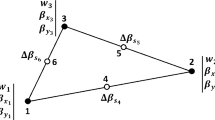
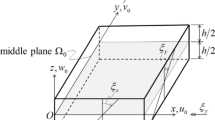
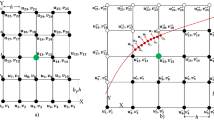
In this article we focus on the approximation of the Reissner–Mindlin (R–M) plate model by high-order p and hp versions of the Finite Element Method (FEM), in the case when the mesh includes curved elements; this is of particular interest when plates with smooth boundary are considered. Our main goal is to verify that an appropriately defined Mixed Interpolated Tensorial Components (MITC) FEM performs well, in the presence of curved elements, when the energy norm is used as an error measure, as well as when quantities of engineering interest are computed. Comments on the performance of the standard FEM formulation are also made

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ainsworth M., and Pinchedez K. (2002). hp-MITC finite element method for the Reissner-Mindlin plate problem. J. Comp. Appl. Math. 148:429–462

    Article  MathSciNet  Google Scholar 

  2. Arnold D., and Falk S. (1989). Edge effects in the Reissner-Mindlin plate theory. In Noor A.K., Belytschko T., and Simo J.C (eds). Analytic and Computational Models of Shells. A.S.M.E., New York, pp. 71–90

    Google Scholar 

  3. Brezzi F., Bathe K.J., and Fortin M. (1989). Mixed-interpolated elements for Reissner-Mindlin plates. Int. J. Numer. Methods Engrg. 28:1787–1801

    Article  MathSciNet  Google Scholar 

  4. Chilton L., and Suri M. (2000). On the construction of stable curvilinear p version elements for mixed formulations of elasticity and Stokes flow. Numer. Math. 86:29–48

    Article  MathSciNet  Google Scholar 

  5. Kurtz J. (2002). A p-version Finite Element Method for Shear Force Computation in Reissner-Mindlin Plates with Curved Boundary. M.Sc. Thesis, Department of Mathematics and Computer Science, Clarkson University, Potsdam, NY

    Google Scholar 

  6. Kurtz J., and Xenophontos C. (2003). On the effects of using curved elements in the approximation of the Reissner-Mindlin plate by the p version of the finite element method. Appl. Num. Math. 46:231–246

    Article  MathSciNet  Google Scholar 

  7. Rank E., Krause R., and Preusch K. (1998). On the accuracy of p-version elements for the Reissner-Mindlin plate model. Int. J. Numer. Meth. Engrg. 43:51–67

    Article  Google Scholar 

  8. Schwab Ch., Suri M., and Xenophontos C. (1998). The hp finite element method for problems in mechanics with boundary layers. Comput. Methods Appl. Mech. Engrg. 157:311–333

    Article  MathSciNet  Google Scholar 

  9. Stenberg R., and Suri M. (1997). An hp error analysis of MITC plate elements. SIAM J. Num. Anal. 34:544–568

    Article  MathSciNet  Google Scholar 

  10. Suri M. (1996). Analytic and computational assessment of locking in the hp finite element method. Comput. Meth. Appl. Mech. Engrg. 133:347–371

    Article  MATH  MathSciNet  Google Scholar 

  11. Suri M., Babuška I., and Schwab C. (1995). Locking effects in the finite element approximation of plate models. Math. Comp. 64:461–482

    Article  MathSciNet  Google Scholar 

  12. Szabó, B., and Babuška, I. (1991). Finite Element Analysis, Wiley

  13. Xenophontos, C., Kurtz, J., and Fulton, S. R. (2003). A hp MITC finite element method for Reissner-Mindlin plates with smooth boundaries, Technical Report 2003–01, Department of Mathematical and Computer Science, Clarkson University

Download references

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Loyola College, 4501 N. Charles Street, Baltimore, MD, 21210, USA

    Christos Xenophontos

Authors
  1. Christos Xenophontos
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Christos Xenophontos.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xenophontos, C. The Use of Curved Elements in the Finite Element Approximation of Thin Plates by High Order p and hp Methods. J Sci Comput 27, 465–476 (2006). https://doi.org/10.1007/s10915-005-9053-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-005-9053-9

Keywords

Profiles

  1. Christos Xenophontos View author profile