Skip to main content
SpringerLink
Log in

Constraint-Free Adaptive FEMs on Quadrilateral Nonconforming Meshes

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

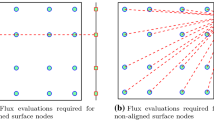
Abstract

Finite element methods (FEMs) on nonconforming meshes have been much studied in the literature. In all earlier works on such methods , some constraints must be imposed on the degrees of freedom on the edge/face with hanging nodes in order to maintain continuity, which make the numerical implementation more complicated. In this paper, we present two FEMs on quadrilateral nonconforming meshes which are constraint-free. Furthermore, we establish the corresponding residual-based a posteriori error reliability and efficiency estimation for general quadrilateral meshes. We also present extensive numerical testing results to systematically compare the performance among three adaptive quadrilateral FEMs: the constraint-free adaptive \(\mathbb Q _1\) FEM on quadrilateral nonconforming meshes with hanging nodes developed herein, the adaptive \(\mathbb Q _1\) FEM based on quadrilateral red-green refinement without any hanging node recently proposed in Zhao et al. (SIAM J Sci Comput 3(4):2099–2120, 2010), and the classical adaptive \(\mathbb Q _1\) FEM on quadrilateral nonconforming meshes with constraints on hanging nodes. Some extensions are also included in this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. Here we do not consider the adaptive moving-mesh method, which can be used on quadrilateral and hexahedral meshes without any hanging nodes.

  2. For the classical constrained FEMs on nonconforming meshes, there are two approaches to assemble stiffness matrix. One is assembling a saddle matrix through an elementwise computation which is based the original bases functions including bases function on hanging nodes, and then eliminating the constraints in the saddle matrix to reduce to a symmetric matrix (the bilinear form is symmetric). The other one is modifying the bases functions as a“macro-element” on regular nodes (add a half of the basis function on a hanging node to the two bases functions on the corresponding two regular nodes, see (5.6) in [30]) and remove all the bases functions on hanging nodes, and then assembling the stiffness matrix with the modified bases functions on regular nodes, which automatically generates a symmetric matrix (the bilinear form is symmetric). Cite Sect. 5 in [30]. However, the well-used element-wise assembly technique is lost in assembling stiffness matrix in the latter approach if using modified bases functions.

References

  1. Ainsworth, M.: Robust a posteriori error estimation for nonconforming finite element approximation. SIAM J. Numer. Anal. 42, 2320–2341 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  2. Ainsworth, M., Demkowicz, L., Kim, C.W.: Analysis of the equilibrated residual method for a posteriori error estimation on meshes with hanging nodes. Comput. Methods Appl. Mech. Eng. 196, 3493–3507 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  3. Ainsworth, M., Oden, J.T.: A posteriori error estimation in finite element analysis. In: Pure and Applied Mathematics. Wiley-Interscience, Wiley, New York (2000)

  4. Alonso, A.: Error estimators for a mixed method. Numer. Math. 74(4), 385–395 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  5. Arnold, D.N., Mukherjee, A., Pouly, L.: Locally adapted tetrahedral meshes using bisection. SIAM J. Sci. Comput. 22(2), 431–448 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  6. Babuska, I., Rheinboldt, W.C.: Error estimates for adaptive finite element computations. SIAM J. Numer. Anal. 15, 736–754 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bank, R.E., Sherman, A.H., Weiser, A.: Refinement algorithms and data structures for regular local mesh refinement, scientific computing. In: Stepleman, R.S. (ed.) Applications of Mathematics and Computing to the Physical Sciences, pp. 3–17. North-Holland, Amsterdam (1993)

    Google Scholar 

  8. Bänsch, E.: Local mesh refinement in 2 and 3 dimensions. Impact Comput. Sci. Eng. 3, 181–191 (1991)

    Article  MATH  Google Scholar 

  9. Binev, P., Dahmen, W., DeVore, R.: Adaptive finite element methods with convergence rates. Numer. Math. 97, 219–268 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  10. Carstensen, C.: A posteriori error estimate for the mixed finite element method. Math. Comp. 66(218), 465–476 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  11. Carstensen, C., Bartels, S., Jansche, S.: A posteriori error estimates for nonconforming finite element methods. Numer. Math. 92, 233–256 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  12. Carstensen, C., Hu, Jun: A unifying theory of a posteriori error control for nonconforming finite element methods. Numer. Math. 107, 473–502 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  13. Chen, Z., Dai, S.: On the efficiency of adaptive finite element methods for elliptic problems with discontinuous coefficients. SIAM J. Sci. Comput. 24, 443–462 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  14. Choi, C.K., Park, Y.M.: Nonconforming transition plate bending elements with variable mid-side nodes. Comput. Struct. 32, 295–304 (1989)

    Article  MATH  Google Scholar 

  15. Dari, E., Duran, R., Padra, C.: Error estimators for nonconforming finite element approximations of the Stokes problem. Math. Comp. 64(211), 1017–1033 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  16. Dari, E., Duran, R., Padra, C., Vampa, V.: A posteriori error estimators for nonconforming finite element methods. Math. Model. Numer. Anal. 30, 385–400 (1996)

    MATH  MathSciNet  Google Scholar 

  17. Heuveline, V., Schieweck, F.: \(H^1\) -interpolation on quadrilateral and hexahedral meshes with hanging nodes. Computing 80, 203–220 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  18. Huang, F., Xie, X.: A modified nonconforming 5-node quadrilateral transition finite element. Adv. Appl. Math. Mech. 2(6), 784–797 (2010)

    MATH  MathSciNet  Google Scholar 

  19. Kellogg, R.B.: On the Poisson equation with intersecting interfaces. Appl. Anal. 4, 101–129 (1975)

    Article  MathSciNet  Google Scholar 

  20. Kossaczký, I.: A recursive approach to local mesh refinement in two and three dimensions. J. Comput. Appl. Math. 55, 275–288 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  21. Leitner, E., Selberherr, S.: Three-dimensional grid adaptation using a mixed-element decomposition method. In: Ryssel, H., Pichler, P. (eds.) Simulation of Semiconductor Devices and Processes, vol. 6, pp. 464–467. Springer, Berlin (1995)

  22. Maubach, J.: Local bisection refinement for n-simplicial grids generated by reflection. SIAM J. Sci. Comput. 16(1), 210–227 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  23. Mitchell, W.F.: Adaptive refinement for arbitrary finite element spaces with hierarchical basis. J. Comput. Appl. Math. 36, 65–78 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  24. Molino, N., Bridson, R., Teran, J., Fedkiw, R.: A Crystalline, Red Green Strategy for Meshing Highly Deformable Objects with tetrahedra. In: 12th international meshing roundtable. Sandia National Laboratories pp 103–114 (2003)

  25. Morin, P., Nochetto, R.H., Siebert, K.G.: Data oscillation and convergence of adaptive FEM. SIAM J. Numer. Anal. 38, 466–488 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  26. Plaza, A., Carey, G.F.: Local refinement of simplicial grids based on the skeleton. Appl. Numer. Math. 32(2), 195–218 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  27. Rivara, M.C.: Mesh refinement processes based on the generalized bisection of simplices. SIAM J. Numer. Anal. 21, 604–613 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  28. Rivara, M.C., Iribarren, G.: The 4-triangles longest-side partition of triangles and linear refinement algorithms. Math. Comput. 65(216), 1485–1501 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  29. Rosenberg, I.G., Stenger, F.: A lower bound on the angles of triangles constructed by biseciting the longest side. Math. Comp. 29, 390–395 (1975)

    Article  MATH  MathSciNet  Google Scholar 

  30. Zhao, X.Y., Mao, S.P., Shi, Z.C.: Adaptive quadrilateral and hexahedral finite element methods with hanging nodes and convergence analysis. J. Comput. Math. 28(5), 621–644 (2010)

    MATH  MathSciNet  Google Scholar 

  31. Zhao, X.Y., Mao, S.P., Shi, Z.C.: Adaptive finite element methods on quadrilateral meshes without hanging nodes. SIAM J. Sci. Comput. 32(4), 2099–2120 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  32. Zhao, X.Y.: Red-green-type refinements, nonconforming elements, quadrilateral hanging-node-free and constraint-free adaptive methods (in Chinese). PhD dissertation, Library of Academy of mathematics and systems science, Chinese Academy of Sciences, May (2010)

Download references

Acknowledgments

The research was supported by National Nature Science Foundation of China grant 11201462, and National Nature Science Foundation of China grant 11371359, and U.S. Department of Energy grant DE-SC0005346, and U.S. NSF grant DMS-1016073.

Author information

Authors and Affiliations

  1. LSEC, Institute of Computational Mathematics and Scientific/Engineering Computing, NCMIS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, People’s Republic of China

    Xuying Zhao & Zhong-Ci Shi

  2. Department of Mathematics, Pennsylvania State University, University Park, PA, 16802, USA

    Qiang Du

  3. Beijing Computational Science Research Center, Beijing, 100084, People’s Republic of China

    Xuying Zhao & Qiang Du

Authors
  1. Xuying Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhong-Ci Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qiang Du
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xuying Zhao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, X., Shi, ZC. & Du, Q. Constraint-Free Adaptive FEMs on Quadrilateral Nonconforming Meshes. J Sci Comput 59, 53–79 (2014). https://doi.org/10.1007/s10915-013-9753-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-013-9753-5

Keywords

Mathematics Subject Classification

Search

Navigation