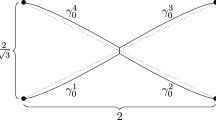
Abstract
We propose a level set framework for representing triple junctions either with or without free endpoints. For triple junctions without free endpoints, our method uses two level set functions to represent the three segments that constitute the structure. For free triple junctions, we extend our method using the free curve work of Schaeffer and Vese (J Math Imaging Vis, 1–17, 2013), Smereka (Phys D Nonlinear Phenom 138(3–4):282–301, 2000). For curves moving under length minimizing flows, it is well known that the endpoints either intersect perpendicularly to the boundary, do not intersect the boundary of the domain or the curve itself (free endpoints), or meet at triple junctions. Although many of these cases can be formulated within the level set framework, the case of free triple junctions does not appear in the literature. Therefore, the proposed free triple junction formulation completes the important curve structure representations within the level set framework. We derive an evolution equation for the dynamics of the triple junction under length and area minimizing flow. The resulting system of partial differential equations are both coupled and highly non-linear, so the system is solved numerically using the Sobolev preconditioned descent. Qualitative numerical experiments are presented on various triple junction and free triple junction configurations, as well as an example with a quadruple junction instability. Quantitative results show convergence of the preconditioned algorithm to the correct solutions.










Similar content being viewed by others
References
Almgren, F., Taylor, J., Wang, L.: Curvature-driven flows: a variational approach. SIAM J. Control Optim. 31(2), 387–438 (1993)
Ambrosio, L., Tortorelli, V.M.: Approximation of functional depending on jumps by elliptic functional via t-convergence. Commun. Pure Appl. Math. 43(8), 999–1036 (1990)
Bar, L., Sapiro, G.: Generalized Newton-type methods for energy formulations in image processing. SIAM J. Imaging Sci. 2(2), 508 (2009)
Bucur, D., Buttazzo, G., Varchon, N.: On the problem of optimal cutting. SIAM J. Optim. 13(1), 157–167 (2002)
Caselles, R., Kimmel, V., Sapiro, G.: Geodesic active contours. Int. J. Comput. Vis. 22(1), 61–79 (1997)
Chan, T.F., Sandberg, B.Y., Vese, L.A.: Active contours without edges for vector-valued images. J. Vis. Commun. Image Represent. 11(2), 130–141 (2000)
Chan, T.F., Vese, L.A.: Active contours without edges. IEEE Trans. Image Process. 10(2), 266–277 (2001)
Chung, G., Vese, L.A.: Energy minimization based segmentation and denoising using a multilayer level set approach. In: Energy Minimization Methods in Computer Vision and Pattern Recognition, pp. 439–455. Springer, Berlin (2005)
Cohen, L.D., Kimmel, R.: Global minimum for active contour models: a minimal path approach. Int. J. Comput. Vis. 24(1), 57–78 (1997)
Concus, P., Golub, G.H.: Use of fast direct methods for the efficient numerical solution of nonseparable elliptic equations. SIAM J. Numer. Anal. 10(6), 1103–1120 (1973)
Crandall, M.G., Evans, L.C., Gariepy, R.F.: Optimal lipschitz extensions and the infinity laplacian. Calc. Var. Partial Differ. Equ. 13(2), 123–139 (2001)
Dal Maso, G., Toader, R.: A model for the quasi-static growth of brittle fractures based on local minimization. ArXiv Mathematics e-prints, June (2002)
Esedoglu, S., Ruuth, S., Tsai, R.: Diffusion generated motion using signed distance functions. J. Comput. Phys. 229(4), 1017–1042 (2010)
Esedoglu, S., Smereka, P.: A variational formulation for a level set representation of multiphase flow and area preserving curvature flow. Commun. Math. Sci. 6(1), 125–148 (2008)
Evans, L.C., Gariepy, R.F.: Measure Theory and Fine Properties of Functions. CRC Press, Boca Raton, FL (1992)
Evans, L.C., Yu, Y.: Various properties of solutions of the Infinity-Laplacian equation. Commun. Partial Differ. Equ. 30(9), 1401–1428 (2005)
Jung, M., Chung, G., Sundaramoorthi, G., Vese, L.A., Yuille, A.L.: Sobolev gradients and joint variational image segmentation, denoising, and deblurring. Proc. SPIE, 7246(1), 72460I–72460I-13 (2009)
Kass, M., Witkin, A., Terzopoulos, D.: Snakes: active contour models. Int. J. Comput. Vis. 1(4), 321–331 (1988)
Kimmel, R., Bruckstein, A.M.: Regularized laplacian zero crossings as optimal edge integrators. Int. J. Comput. Vis. 53, 225–243 (2001)
Lacoste, C., Descombes, X., Zerubia, J.: Unsupervised line network extraction in remote sensing using a polyline process. Pattern Recogn. 43(4), 1631–1641 (2010)
Larsen, C.J., Richardson, C.L., Sarkis, M.: A level set method for the mumford -Shah functional and fracture. Preprint serie A, Instituto Nacional de Matemática Pura e Aplicada, Brazilian Ministry for Science and Technology (2008)
Li, H., X-C T.: Piecewise constant level set methods for multiphase motion. Int. J. Numer. Anal. Mod. 4(2), 291–305 (2007)
Lu, G., Wang, P.: Inhomogeneous infinity laplace equation. Adv. Math. 217(4), 1838–1868 (2008)
Melonakos, J., Pichon, E., Angenent, S., Tannenbaum, A.: Finsler active contours. Pattern Anal. Mach. Intell. IEEE Trans. 30(3), 412–423 (2008)
Merriman, B., Bence, J.K., Osher, S.J.: Motion of multiple junctions: a level set approach. J. Comput. Phys. 112(2), 334–363 (1994)
Mumford, D., Shah, J.: Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 42(5), 577–685 (1989)
Neuberger, J.W.: Sobolev Gradients and Differential Equations. Springer, Berlin (2009)
Oberman, A.M.: A convergent difference scheme for the infinity laplacian: construction of absolutely minimizing lipschitz extensions. Math. Comput. 74(251), 1217–1230 (2004)
Osher, S., Sethian, J.A.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 79(1), 12–49 (1988)
Reitich, F., Soner, H.M.: Three-phase boundary motion under constant velocities i: the vanishing surface tension limit. Proc. R. Soc. Edinb. 126A, 837–865 (1997)
Renka, R.J.: A simple explanation of the sobolev gradient method (2006). http://www.cse.unt.edu/~renka/papers/sobolev.pdf
Richardson, W.B.: Sobolev gradient preconditioning for image-processing PDEs. Commun. Numer. Methods Eng. 24(6), 493–504 (2006)
Ruuth, S.J.: A diffusion-generated approach to multiphase motion. J. Comput. Phys. 145(1), 166–192 (1998)
Ruuth, S.J.: Efficient algorithms for diffusion-generated motion by mean curvature. J. Comput. Phys. 144(2), 603–625 (1998)
Schaeffer, H.: Active arcs and contours. UCLA CAM Report, pp. 12–54 (2012)
Schaeffer, H., Vese, L.: Active contours with free endpoints. J. Math. Imaging Vis. (2013). doi:10.1007/s10851-013-0437-4
Smereka, P.: Spiral crystal growth. Phys. D Nonlinear Phenom. 138(3–4), 282–301 (2000)
Smereka, P.: Semi-implicit level set methods for curvature and surface diffusion motion (english). J. Sci. Comput. 19(1–3), 439–456 (2003)
Smith, K.A., Solis, F.J., Chopp, D.: A projection method for motion of triple junctions by level sets. Interfaces Free Boundaries 4(3), 263–276 (2002)
Sundaramoorthi, G., Yezzi, A., Mennucci, A.C.: Sobolev active contours. Int. J. Comput. Vis. 73(3), 345–366 (2007)
Sussman, M., Smereka, P., Osher, S.: A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 114(1), 146–159 (1994)
Taylor, J.E.: A variational approach to crystalline triple-junction motion. J. Stat. Phys. 95, 1221–1244 (1999). doi:10.1023/A:1004523005442
Taylor, J.E.: The motion of multiple-phase junctions under prescribed phase-boundary velocities. J. Differ. Equ. 119(1), 109–136 (1995)
Vese, L.A., Chan, T.F.: A multiphase level set framework for image segmentation using the mumford and shah model. Int. J. Comput. Vis. 50(3), 271–293 (2002)
Zhao, H.-K., Chan, T., Merriman, B., Osher, S.: A variational level set approach to multiphase motion. J. Comput. Phys. 127(1), 179–195 (1996)
Acknowledgments
This research was made possible by the Department of Defense (DoD) through the National Defense Science and Engineering Graduate Fellowship (NDSEG) and by NSF DMS 1217239. The authors would like to thank Selim Esedoglu for his helpful discussion and the reviewers and editor for their useful comments. The authors would also like to thank Stanley Osher for his helpful comments.
Author information
Authors and Affiliations
Corresponding author
Appendix: Derivation of the First Variation for Free Triple Junctions
Appendix: Derivation of the First Variation for Free Triple Junctions
Let \(\phi ,\psi , \nu \in W^{1,\infty }\), recall the free triple junction Length function
To compute the first variation, let \(w \in W^{1,\infty }\) and differentiate the energy with respect to perturbation using these functions. First, to find the minimizer \(\phi \), we fix \(\psi \) and \(\nu \) and define \(G(\varepsilon ):=L_{fT}(\phi +\varepsilon w,\psi ,\nu )\) and compute \(G'(0)=0\).
Next setting \(\varepsilon =0\) and integrating by parts (with \(\frac{\partial \phi }{\partial n}=0\) on \(\partial \varOmega \)):
Since this holds for all \(w\), the first variation is:
and can be embedded in a time-dependent descent:
Next, to find the minimizer \(\psi \), we fix \(\phi \) and \(\nu \) and define \(G(\varepsilon ):=L_{fT}(\phi , \psi +\varepsilon w,\nu )\) and compute \(G'(0)=0\) again.
Next setting \(\varepsilon =0\) and integrating by parts (with \(\frac{\partial \psi }{\partial n}=0\) on \(\partial \varOmega \))
Since this holds for all \(w\), the first variation with respect to \(\psi \) is:
and can be embedded in a time-dependent descent:
Lastly, to find the minimizer \(\nu \), we may repeat the previous procedure. Note that since in terms of \(\nu \) the functional is:
with \(F(\phi ,\psi )=l_{+} |\nabla H(\phi )| H(\psi ) + l_{-} |\nabla H(\phi )| H(-\psi ) + l_{0} |\nabla H(\psi )| H(\phi ) \), then the first variation is \(\langle F(\phi ,\psi ), \delta (\nu )\rangle _{L^2}=0\). Embedding the equation in a descent differential equation yields:
Rights and permissions
About this article
Cite this article
Schaeffer, H., Vese, L. Variational Dynamics of Free Triple Junctions. J Sci Comput 59, 386–411 (2014). https://doi.org/10.1007/s10915-013-9767-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-013-9767-z