Skip to main content
Springer Nature Link
Log in

Shape Optimization by Free-Form Deformation: Existence Results and Numerical Solution for Stokes Flows

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

Shape optimization problems governed by PDEs result from many applications in computational fluid dynamics. These problems usually entail very large computational costs and require also a suitable approach for representing and deforming efficiently the shape of the underlying geometry, as well as for computing the shape gradient of the cost functional to be minimized. Several approaches based on the displacement of a set of control points have been developed in the last decades, such as the so-called free-form deformations. In this paper we present a new theoretical result which allows to recast free-form deformations into the general class of perturbation of identity maps, and to guarantee the compactness of the set of admissible shapes. Moreover, we address both a general optimization framework based on the continuous shape gradient and a numerical procedure for solving efficiently three-dimensional optimal design problems. This framework is applied to the optimal design of immersed bodies in Stokes flows, for which we consider the numerical solution of a benchmark case study from literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Notes

  1. Nevertheless, the FFD technique presents some drawbacks; for instance, it is not possible to change the topology of the control points lattice, FFD it is not interpolatory, and the choice of enabled displacements is application dependent (as it happens with other common parameterizations).

  2. The set \({\mathcal {O}}\) can be endowed with the convergence in the sense of the characteristic functions or in the sense of Hausdorff—see e.g. [17] for definitions.

  3. A notion of derivative of a cost functional with respect to the domain can be introduced for the shape deformation with perturbation of identity maps. In particular, recall [17, 34, 39] that the Eulerian derivative of \(J: {\mathcal {O}}_{\mathcal {T}}(\varOmega ) \rightarrow \mathbb {R}\), in \(\varOmega \) and direction \(\varvec{\theta }\) is defined as

    $$\begin{aligned} dJ(\varOmega ; \varvec{\theta }) = \lim _{t \rightarrow 0} \frac{1}{t}[{J(({{\varvec{I}}} + t \varvec{\theta })(\varOmega ))-J(\varOmega )}]. \end{aligned}$$

  4. A large absolute value for the mean \(E_i\) implies that \(\mu _i\) has an important overall effect on the output, whereas a high standard deviation \(S_i\) indicates that the effect of \(\mu _i\) is not constant, which may be implied by a parameter interacting with other parameters.

  5. Thanks to the formulation (7) and the definition of Bernstein polynomials, it is easy to check that the boundary of \(D\) can be deformed only by control points belonging to \(\partial \widehat{D}\).

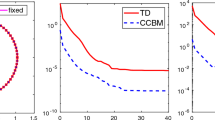
  6. Most of the CPU time is spent in the backtracking procedure to seek a step-length \(\alpha ^{(n)}\) fulfilling Armijo’s rule (33), which, once a near-optimal shape is found at the first iteration, is verified only for very small \(\alpha ^{(n)}\). This explains the large number of evaluations of \(j(\tilde{\varvec{\mu }})\).

References

  1. Allaire, G.: Conception Optimale de Structures. Springer, Berlin (2007)

    MATH  Google Scholar 

  2. Amoiralis, E.I., Nikolos, I.K.: Freeform deformation versus B-spline representation in inverse airfoil design. J. Comput. Inf. Sci. Eng. 8(2), 1–13 (2008)

    Article  Google Scholar 

  3. Andreoli, M., Janka, A., Désidéri, J.A.: Free-form-deformation parametrization for multilevel 3D shape optimization in aerodynamics. Technical Report 5019, INRIA Sophia Antipolis (2003)

  4. Bello, J.A., Fernández-Cara, E., Lemoine, J., Simon, J.: The differentiability of the drag with respect to the variations of a Lipschitz domain in a Navier–Stokes flow. SIAM J. Control Optim. 35, 626–640 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  5. Bertsekas, D.P.: On the Goldstein–Levitin–Polyak gradient projection method. IEEE Trans. Autom. Control 21(2), 174–184 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bourot, J.-M.: On the numerical computation of the optimum profile in Stokes flow. J. Fluid Mech. 65(3), 513–515 (1974)

    Article  MATH  Google Scholar 

  7. Burman, E., Fernández, M.A.: Continuous interior penalty finite element method for the time-dependent Navier–Stokes equations: space discretization and convergence. Numer. Math. 107(1), 39–77 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  8. Campolongo, F., Cariboni, J., Saltelli, A.: An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 22(10), 1509–1518 (2007)

    Article  Google Scholar 

  9. Céa, J.: Conception optimale ou identification de formes, calcul rapide de la dérivée directionnelle de la fonction coût. Math. Model. Num. Anal. 20(3), 371–402 (1986)

    MATH  MathSciNet  Google Scholar 

  10. Farin, G.: Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide. Morgan Kaufmann, Los Altos (2001)

    Google Scholar 

  11. Gain, J., Bechmann, D.: A survey of spatial deformation from a user-centered perspective. ACM Trans. Graph. 27(4), 107:1–107:21 (2008)

    Article  Google Scholar 

  12. Gain, J.E., Dodgson, N.A.: Preventing self-intersection under free-form deformation. IEEE Trans. Vis. Comput. Graph. 7(4), 289–298 (2001)

    Article  Google Scholar 

  13. Gunzburger, M.D.: Perspectives in Flow Control and Optimization. SIAM, Philadelphia (2003)

    MATH  Google Scholar 

  14. Gunzburger, M.D., Hou, L., Svobodny, T.P.: Boundary velocity control of incompressible flow with an application to viscous drag reduction. SIAM J. Control Optim. 30, 167 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  15. Gunzburger, M.D., Kim, H., Manservisi, S.: On a shape control problem for the stationary Navier–Stokes equations. ESAIM Math. Model. Numer. Anal. 34(6), 1233–1258 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  16. Haslinger, J., Mäkinen, R.A.E.: Introduction to Shape Optimization: Theory, Approximation, and Computation. SIAM, Philadelphia (2003)

    Book  Google Scholar 

  17. Henrot, A., Pierre, M.: Variation et Optimisation de Formes: Une Analyse Géométrique. Springer, Berlin (2005)

    Book  Google Scholar 

  18. Henrot, A., Privat, Y.: What is the optimal shape of a pipe? Arch. Ration. Mech. Anal. 196(1), 281–302 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  19. Jameson, A.: Aerodynamic design via control theory. J. Sci. Comput. 3(3), 233–260 (1988)

    Article  MATH  Google Scholar 

  20. Jameson, A.: Optimum aerodynamic design using CFD and control theory. In: Proceedings of the 12th AIAA Computational Fluid Dynamics Conference, pp. 926–949. AIAA Paper 95–1729 (1995)

  21. Lamousin, H.J., Waggenspack, W.N.: NURBS-based free-form deformations. IEEE Comput. Graph. Appl. 14(6), 59–65 (1994)

    Article  Google Scholar 

  22. Lassila, T., Rozza, G.: Parametric free-form shape design with PDE models and reduced basis method. Comput. Methods Appl. Mech. Eng. 199(23–24), 1583–1592 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  23. Lehnhäuser, T., Schäfer, M.: A numerical approach for shape optimization of fluid flow domains. Comput. Methods Appl. Mech. Eng. 194, 5221–5241 (2005)

    Article  MATH  Google Scholar 

  24. Lombardi, M., Parolini, N., Quarteroni, A., Rozza, G.: Numerical simulation of sailing boats: dynamics, FSI, and shape optimization. In: Buttazzo, G., Frediani, A. (eds.) Variational Analysis and Aerospace Engineering: Mathematical Challenges for Aerospace Design. Contributions from a Workshop Held at the School of Mathematics in Erice, Italy, volume 66 of Springer Optimization and Its Applications (2012)

  25. Manzoni, A.: Reduced models for optimal control, shape optimization and inverse problems in haemodynamics. Ph.D. Thesis, N. 5402, École Polytechnique Fédérale de Lausanne, 2012.

  26. Manzoni, A., Quarteroni, A., Rozza, G.: Shape optimization of cardiovascular geometries by reduced basis methods and free-form deformation techniques. Int. J. Numer. Methods Fluids 70(5), 646–670 (2012)

    Article  MathSciNet  Google Scholar 

  27. Mohammadi, B., Pironneau, O.: Optimal shape design for fluids. Annu. Rev. Fluids Mech. 36, 255–279 (2004)

    Article  MathSciNet  Google Scholar 

  28. Mohammadi, B., Pironneau, O.: Applied shape optimization for fluids. Numerical Mathematics and Scientific Computation. Oxford Univ. Press, New York (2010)

  29. Morris, M.D.: Factorial sampling plans for preliminary computational experiments. Technometrics 33(2), 161–174 (1991)

    Article  Google Scholar 

  30. Murat, F., Simon, J.: Sur le contrôle par un domaine géométrique. Internal Report No. 76 015, Laboratoire d’Analyse Numérique de l’Université Paris 6, (1976)

  31. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York (1999)

    Book  MATH  Google Scholar 

  32. Ogawa, Y., Kawahara, M.: Shape optimization of body located in incompressible viscous flow based on optimal control theory. Int. J. Comput. Fluid Dyn. 17, 243–251 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  33. Pironneau, O.: On optimum profiles in Stokes flow. J. Fluid Mech. 59(1), 117–128 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  34. Pironneau, O.: Optimal Shape Design for Elliptic Systems, Springer Series in Computational Physics. Springer, New York (1984)

    Book  Google Scholar 

  35. Richardson, S.: Optimum profiles in two-dimensional Stokes flow. Proc. Math. Phys. Sci. 450(1940), 603–622 (1995)

    Article  MATH  Google Scholar 

  36. Samareh, J.A.: Aerodynamic shape optimization based on free-form deformation. Proc. 10th AIAA/ISSMO Multidiscip. Anal. Optim. Conf. 6, 3672–3683 (2004)

    Google Scholar 

  37. Sarakinos, S.S., Amoiralis, E., Nikolos, I.K.: Exploring freeform deformation capabilities in aerodynamic shape parameterization. Proc. Int. Conf. Comput. Tool 1, 535–538 (2005)

    Google Scholar 

  38. Sederberg, T.W., Parry, S.R.: Free-form deformation of solid geometric models. Comput. Graph. 20(4), 151–160 (1986)

    Article  Google Scholar 

  39. Sokolowski, J., Zolésio, J.-P.: Introduction to Shape Optimization: Shape Sensitivity Analysis. Springer, New York (1992)

    Book  MATH  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the collaboration with Prof. Alfio Quarteroni (CMCS, EPFL and MOX, Politecnico di Milano) and Dr. Toni Lassila (CMCS, EPFL) for their insights, useful discussions and support. We acknowledge the use of the finite element library LifeV (www.lifev.org) as a basis for the numerical simulations presented in this paper. Computational support from Consorzio Interuniversitario Lombardo per l’Elaborazione Automatica (CILEA) computing facilities under the LISA initiative is also acknowledged. This work has been partially funded by the Swiss National Science Foundation (Projects 122136 and 135444) and by the SHARM 2012–2014 SISSA post-doctoral research grant on the Project “Reduced Basis Methods for shape optimization in computational fluid dynamics”.

Author information

Authors and Affiliations

  1. MOX-Modellistica e Calcolo Scientifico, Dipartimento di Matematica “F. Brioschi”, Politecnico di Milano, P.za Leonardo da Vinci 32, 20133 , Milano, Italy

    Francesco Ballarin

  2. SISSA Mathlab, Scuola Internazionale Superiore di Studi Avanzati, via Bonomea 265, 34136 , Trieste, Italy

    Andrea Manzoni & Gianluigi Rozza

  3. Dipartimento di Matematica “F. Brioschi”, Politecnico di Milano, P.za Leonardo da Vinci 32, 20133 , Milano, Italy

    Sandro Salsa

Authors
  1. Francesco Ballarin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Andrea Manzoni
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gianluigi Rozza
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Sandro Salsa
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Andrea Manzoni.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ballarin, F., Manzoni, A., Rozza, G. et al. Shape Optimization by Free-Form Deformation: Existence Results and Numerical Solution for Stokes Flows. J Sci Comput 60, 537–563 (2014). https://doi.org/10.1007/s10915-013-9807-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-013-9807-8

Keywords

Mathematics Subject Classification