Skip to main content
Springer Nature Link
Log in

High-Order Flux Reconstruction Schemes with Minimal Dispersion and Dissipation

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

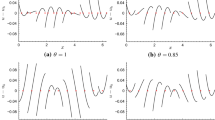
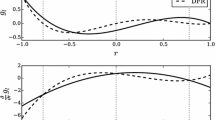
Modal analysis of the flux reconstruction (FR) formulation is performed to obtain the semi-discrete and fully-discrete dispersion relations, using which, the wave properties of physical as well as spurious modes are characterized. The effect of polynomial order, correction function and solution points on the dispersion, dissipation and relative energies of the modes are investigated. Using this framework, a new set of linearly stable high-order FR schemes is proposed that minimizes wave propagation errors for the range of resolvable wavenumbers. These schemes provide considerably reduced error for advection in comparison to the Discontinuous Galerkin scheme and benefit from having an explicit differential update. The corresponding resolving efficiencies compare favorably to those of standard high-order compact finite difference schemes. These theoretical expectations are verified by a comparison of proposed and existing FR schemes in advecting a scalar quantity on uniform as well as non-uniform grids.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

References

  1. Tam, C.K.W.: Computational aeroacoustics: issues and methods. AIAA J. 33(10), 1788–1796 (1995)

    Article  MATH  Google Scholar 

  2. Visbal, M.R., Gaitonde, D.V.: Very high-order spatially implicit schemes for computational acoustics on curvilinear meshes. J. Comp. Acous. 09, 1259 (2001)

    Article  MathSciNet  Google Scholar 

  3. Wang, M., Freund, J.B., Lele, S.K.: Computational prediction of flow-generated sound. Annu. Rev. Fluid Mech. 38, 483512 (2006)

    Article  MathSciNet  Google Scholar 

  4. Moin, P., Mahesh, K.: Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 53978 (1998)

    Article  MathSciNet  Google Scholar 

  5. Hesthaven, J. S., Warburton, T.: Nodal Discontinuous Galerkin Methods. Springer Texts in Applied Mathematics, 54, (2008)

  6. Lele, S.K.: Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42 (1992)

    Article  MATH  MathSciNet  Google Scholar 

  7. Visbal, M.R., Gaitonde, D.V.: On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 181, 155–185 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  8. Chavent, G., Cockburn, B.: The local projection \(P^0 P^1\)-discontinuous-Galerkin finite element method for scalar conservation laws. RAIRO Model. Math. Anal. Numer. 23, 565 (1989)

    MATH  MathSciNet  Google Scholar 

  9. Lesaint, P., Raviart, P.A.: On a finite element method for solving the neutron transport equation. In: Mathematical Aspects of Finite Elements in Partial Differential Equations, p. 89. Academic Press, San Diego (1974)

  10. Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Los Alamos Scientific Laboratory Report LA-UR-73-479 (1973)

  11. Huynh, H.T.: A flux reconstruction approach to high-order schemes including discontinuous Galerkin methods. In: Huynh, H.T. (ed.) AIAA Conference Paper, 2007–4079 (2007)

  12. Kopriva, D.A., Kolias, J.H.: A conservative staggered-grid Chebyshev multidomain method for compressible flows. J. Comput. Phys. 125, 244–261 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  13. Liu, Y., Vinokur, M., Wang, Z.J.: Spectral difference method for unstructured grids I: basic formulation. J. Comput. Phys. 216, 780–801 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  14. Vincent, P.E., Castonguay, P., Jameson, A.: A new class of high-order energy stable flux reconstruction schemes. J. Sci. Comput. 47(1), 50–72 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  15. Jameson, A., Vincent, P.E., Castonguay, P.: On the non-linear stability of flux reconstruction schemes. J. Sci. Comput. 50(2), 434–445 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  16. Castonguay, P., Vincent, P.E., Jameson, A.: A new class of high-order energy stable flux reconstruction schemes for triangular elements. J. Sci. Comput. 51(1), 224–256 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  17. Huynh, H.T.: High-order methods including discontinuous Galerkin by reconstructions on triangular meshes. In: 49th AIAA Aerospace Sciences Meeting AIAA 2011-44

  18. Williams, D.M., Jameson, A.: Energy stable flux reconstruction schemes for advection-diffusion problems on tetrahedra. J. Sci. Comput. (2013)

  19. Castonguay, P., Williams, D.M., Vincent, P.E., Jameson, A.: Energy stable flux reconstruction schemes for advection-diffusion problems. Comput. Methods Appl. Mech. Eng. 267, 400–417 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  20. Whitham, G.B.: Linear and Nonlinear Waves. Pure and Applied Mathematics, vol. 42. Wiley, New York (2011)

    Google Scholar 

  21. Tam, C.K.W.: Dispersion relation preserving finite difference schemes for computational aeroacoustics. J. Comput. Phys. 107, 262–281 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  22. Adam, Y.: Highly accurate compact implicit methods and boundary conditions. J. Comput. Phys. 24, 10–22 (1977)

    Article  MATH  MathSciNet  Google Scholar 

  23. Haras, Z., Ta’asan, S.: Finite difference schemes for long-time integration. J. Comput. Phys. 114, 265–279 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  24. Hirsch, R.S.: Higher order accurate difference solutions of fluid mechanics problems by a compact differencing technique. J. Comput. Phys. 19, 90–109 (1975)

    Article  Google Scholar 

  25. Sengupta, T.K., Ganeriwal, G., De, S.: Analysis of central and upwind compact schemes. J. Comput. Phys. 192, 677–694 (2003)

    Article  MATH  Google Scholar 

  26. Gottlieb, D., Orszag, S.A.: Numerical Analysis of Spectral Methods. SIAM, Philadelphia (1977)

    Book  MATH  Google Scholar 

  27. Hu, F.Q., Hussaini, M.Y., Rasetarinera, P.: An analysis of the discontinuous Galerkin method for wave propagation problems. J. Comput. Phys. 151, 921946 (1999)

    Article  Google Scholar 

  28. Hu, F.Q., Atkins, H.L.: Eigensolution analysis of the discontinuous Galerkin method with nonuniform grids. J. Comput. Phys. 182, 516–545 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  29. Ainsworth, M.: Dispersive and dissipative behaviour of high order discontinuous Galerkin finite element methods. J. Comput. Phys. 198, 106–130 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  30. Vincent, P.E., Castonguay, P., Jameson, A.: Insights from von Neumann analysis of high-order flux reconstruction schemes. J. Comput. Phys. 230, 81348154 (2011)

    MathSciNet  Google Scholar 

  31. Van den Abeele, K.: Development of High-order Accurate Schemes for Unstructured Grids, Ph.D. thesis, Vrije Universiteit Brussel (2009)

  32. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  33. Powell, M.J.D.: A fast algorithm for nonlinearly constrained optimization calculations. In: Numerical Analysis, Lecture Notes in Mathematics, vol. 630, 144–157. Springer, Berlin (1978)

  34. Optimization Toolbox User’s Guide—Version 5.0, (R2010a), The MathWorks Inc, Natick

  35. Williams, D.M.: Energy stable high-order methods for simulating unsteady, viscous, compressible flows on unstructured grids. Thesis (Ph.D.)-Stanford University (2013)

  36. Carpenter, M.H., Kennedy, C.: Fourth-order 2N-storage Runge–Kutta schemes, Technical Report TM 109112. NASA, NASA Langley Research Center (1994)

  37. Kubatko E. J., Yeager B. A., Ketcheson, D. I.: Optimal strong-stability-preserving Runge-Kutta time discretizations for discontinuous galerkin methods. J. Sci. Comput. doi10.1007/s10915-013-9796-7

Download references

Acknowledgments

The authors are grateful to Prof. S. K. Lele (Professor, Department of Aeronautics and Astronautics, Stanford University) for motivating the problem and advising in the choice of relevant test cases, and to Francisco Palacios (Engineering Research Associate, Department of Aeronautics and Astronautics, Stanford University) for his suggestions regarding the manuscript. The first author would also like to thank David Williams (CFD Engineer, Flight Sciences division, Boeing Commercial Airplanes) and Manuel López (Ph.D. candidate, Department of Aeronautics and Astronautics, Stanford University) for valuable suggestions regarding the optimization problem. The first author was supported in this effort by the Thomas V. Jones Stanford Graduate Fellowship.

Author information

Authors and Affiliations

  1. Department of Aeronautics and Astronautics, Stanford University, Stanford, CA , 94305, USA

    Kartikey Asthana & Antony Jameson

Authors
  1. Kartikey Asthana
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Antony Jameson
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Kartikey Asthana.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Asthana, K., Jameson, A. High-Order Flux Reconstruction Schemes with Minimal Dispersion and Dissipation. J Sci Comput 62, 913–944 (2015). https://doi.org/10.1007/s10915-014-9882-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9882-5

Keywords

Mathematics Subject Classification