Skip to main content
Springer Nature Link
Log in

Generalized Hermite Spectral Method Matching Different Algebraic Decay at infinities

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

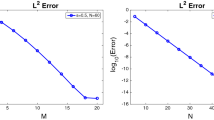
In this paper, we propose a new generalized Hermite spectral method. We introduce an orthogonal family of new generalized Hermite functions, with the weight function \((1+\frac{2}{\pi } \arctan x)^{\alpha }(1-\frac{2}{\pi }\arctan x)^{\gamma }\), \(\alpha \) and \(\gamma \) being arbitrary real numbers. The basic results on the corresponding orthogonal approximation and interpolation are established. As examples of applications, we provide the spectral schemes for a linear problem and the Fisher equation, which possess the spectral accuracy in space and match the different algebraic decay at infinities reasonably. Numerical results demonstrate their high efficiency and coincide well with the analysis.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Boyd, J.P.: The rate of convergence of Hermite function series. Math. Comput. 35, 1309–1316 (1980)

    Article  MATH  Google Scholar 

  2. Boyd, J.P.: The asymptotic coefficients of Hermite series. J. Comput. Phys. 54, 382–410 (1984)

    Article  MATH  Google Scholar 

  3. Fok, J.C.M., Guo, B., Tang, T.: Hermite spectral-finite difference method for the Fokker–Planck equation. Math. Comput. 71, 1497–1528 (2002)

    Article  MATH  Google Scholar 

  4. Funaro, D., Kavian, O.: Approximation of some diffusion evolution equations in unbounded domains by Hermite function. Math. Comput. 57, 597–619 (1999)

    Article  Google Scholar 

  5. Guo, B., Chen, Z.: Analytic solutions of the Fisher equation. J. Phys. A Math. Gen. 24, 645–650 (1991)

    Article  MATH  Google Scholar 

  6. Guo, B.: Spectral Methods and Their Applications. World Scientific, Singapore (1998)

    Book  MATH  Google Scholar 

  7. Guo, B.: Error estimation of Hermite spectral method for nonlinear partial differential equations. Math. Comput. 68, 1067–1078 (1999)

    Article  MATH  Google Scholar 

  8. Guo, B., Xu, C.: Hermite pseudospectral method for nonlinear partial differential equations. Math. Model. Numer. Anal. 34, 859–872 (2000)

    Article  MATH  Google Scholar 

  9. Guo, B., Shen, J., Xu, C.: Spectral and pseudospectral approximations using Hermite functions: application to the Dirac equation. Adv. Comput. Math. 19, 35–55 (2003)

    Article  MATH  Google Scholar 

  10. Guo, B., Shen, J., Wang, L.: Optimal spectral-Galerkin methods using generalized Jacobi polynomials. J. Sci. Comput. 27, 305–322 (2006)

    Article  MATH  Google Scholar 

  11. Guo, B., Shen, J., Wang, L.: Generalized Jacobi polynomials/functions and their applications. Appl. Numer. Math. 59, 1011–1028 (2009)

    Article  MATH  Google Scholar 

  12. Guo, B., Yi, Y.: Generalized Jacobi rational spectral method and its applications. J. Sci. Comput. 43, 201–238 (2010)

    Article  MATH  Google Scholar 

  13. Guo, B., Zhang, C.: Spectral method for high order problems with proper simulations of asymptotic behaviors at infinity. J. Comput. Appl. Math. 237, 269–294 (2013)

    Article  MATH  Google Scholar 

  14. Guo, B.: Some progress in spectral methods. Sci. China Math. 56, 2411–2438 (2013)

    Article  MATH  Google Scholar 

  15. Ma, H., Sun, W., Tang, T.: Hermite spectral methods with a time-dependent scaling for parabolic equations in unbounded domains. SIAM J. Numer. Anal. 43, 58–75 (2005)

    Article  MATH  Google Scholar 

  16. Ma, H., Zhao, T.: A stabilized Hermite spectral method for second-order differential equations in unbounded domain. Numer. Methods PDEs. 23, 968–983 (2007)

    Article  MATH  Google Scholar 

  17. Shen, J., Wang, L.: Some recent advances in spectral methods for unbounded domains. Comm. Comput. Phys. 5, 195–241 (2009)

    Google Scholar 

  18. Sun, T., Guo, B.: Generalized Jacobi approximation in multiple dimensions and its applications. J. Sci. Comput. 55, 327–350 (2013)

    Article  MATH  Google Scholar 

  19. Weideman, J.A.C.: The eigenvalues of Hermite and rational differentiation matrices. Numer. Math. 61, 409–431 (1992)

    Article  Google Scholar 

  20. Xiang, X., Wang, Z.: Generalized Hermite spectral method and its applications to problems in unbounded domains. SIAM J. Numer. Anal. 48, 1231–1253 (2010)

    Article  MATH  Google Scholar 

  21. Yi, Y., Guo, B.: Generalized Jacobi rational spectral method on the half line. Adv. Math. Comput. 37, 1–37 (2012)

    Article  MATH  Google Scholar 

  22. Zhang, C., Guo, B.: Generalized Hermite spectral method matching asymptotic behaviors. J. Comput. Appl. Math. 255, 616–634 (2014)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Shanghai Normal University, Shanghai, 200234, China

    Ben-yu Guo

  2. Scientific Computing Key Laboratory of Shanghai Universities, Division of Computational Science of E-institute of Shanghai Universities, Shanghai, China

    Ben-yu Guo

  3. Jiangsu Normal University, Xuzhou, 221116, China

    Chao Zhang

Authors
  1. Ben-yu Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chao Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ben-yu Guo.

Additional information

The work of Chao Zhang is supported in part by NSF of China N.11171227 and N.11371123, Research Fund for Young Teachers of Jiangsu Normal University N.11XLR27, and Priority Academic Program Development of Jiangsu Higher Education Institutions.

The work of Ben-yu Guo is supported in part by NSF of China N.11171227, Fund for Doctoral Authority of China N.20123127110001, Fund for E-institute of Shanghai Universities N.E03004, and Leading Academic Discipline Project of Shanghai Municipal Education Commission N.J50101.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Guo, By., Zhang, C. Generalized Hermite Spectral Method Matching Different Algebraic Decay at infinities. J Sci Comput 65, 648–671 (2015). https://doi.org/10.1007/s10915-014-9981-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-014-9981-3

Keywords

Mathematics Subject Classification