Skip to main content
Springer Nature Link
Log in

On Application of the Weak Galerkin Finite Element Method to a Two-Phase Model for Subsurface Flow

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

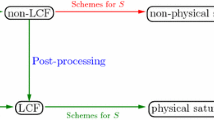
This paper presents studies on applying the novel weak Galerkin finite element method (WGFEM) to a two-phase model for subsurface flow, which couples the Darcy equation for pressure and a transport equation for saturation in a nonlinear manner. The coupled problem is solved in the framework of operator decomposition. Specifically, the Darcy equation is solved by the WGFEM, whereas the saturation is solved by a finite volume method. The numerical velocity obtained from solving the Darcy equation by the WGFEM is locally conservative and has continuous normal components across element interfaces. This ensures accuracy and robustness of the finite volume solver for the saturation equation. Numerical experiments on benchmarks demonstrate that the combined methods can handle very well two-phase flow problems in high-contrast heterogeneous porous media.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Arnold, D.N., Brezzi, F.: Mixed and nonconforming finite element methods: implementation, postprocessing and error estimates. RAIRO Modél. Math. Anal. Numér. 19, 7–32 (1985)

    MathSciNet  MATH  Google Scholar 

  2. Aziz, K., Settari, A.: Petroleum Reservoir Simulation. Applied Science Publishers, Barking (1979)

    Google Scholar 

  3. Bastian, P., Riviere, B.: Superconvergence and \( h(div) \) projection for discontinuous galerkin methods. Int. J. Numer. Methods Fluids 42, 1043–1057 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  4. Brenner, S.C., Scott, L.R.: The Mathematical Theory of Finite Element Methods. Texts in Applied Mathematics, vol. 15, 3rd edn. Springer, New York (2008)

    Book  Google Scholar 

  5. Bush, L., Ginting, V.: On the application of the continuous galerkin finite element method for conservation problems. SIAM J. Sci. Comput. 35, A2953–A2975 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chavent, G., Roberts, J.: A unified physical presentation of mixed, mixed-hybrid finite elements and standard finite difference approximations for the determination of velocities in waterflow problems. Adv. Water Resour. 14, 329–348 (1991)

    Article  Google Scholar 

  7. Chen, Z., Huan, G., Ma, Y.: Computational methods for multiphase flows in porous media. SIAM, Philadelphia (2006)

    Book  MATH  Google Scholar 

  8. Cockburn, B., Gopalakrishnan, J., Wang, H.: Locally conservative fluxes for the continuous galerkin method. SIAM J. Numer. Anal. 45, 1742–1776 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  9. Du, C., Liang, D.: An efficient S-DDM iterative approach for compressible contamination fluid flows in porous media. J. Comput. Phys. 229, 4501–4521 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Efendiev, Y., Galvis, J., Lazarov, R., Margenov, S., Ren, J.: Robust two-level domain decomposition preconditioners for high-contrast anisotropic flows in multiscale media. Comput. Methods Appl. Math. 12, 415–436 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Epshteyn, Y., Riviere, B.: Analysis of hp discontinuous galerkin methods for incompressible two-phase flow. J. Comput. Appl. Math. 225, 487–509 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Ewing, R.: The mathematics of reservoir simulation. SIAM, Philadelphia (1983)

    Book  MATH  Google Scholar 

  13. Healy, R., Russell, T.: Solutions of the advection–dispersion equation in two dimensions by a finite volume Eulerian–Lagrangian localized adjoint method. Adv. Water Resour. 21, 11–26 (1998)

    Article  Google Scholar 

  14. Hou, Z., Engel, D., Lin, G., Fang, Y., Fang, Z.: An uncertainty quantification framework for studying the effect of spatial heterogeneity in reservoir permeability on \({\rm CO}_2\) sequestration. Math. Geosci. 45, 799–817 (2013)

    Article  Google Scholar 

  15. Hughes, T.J.R., Engel, G., Mazzei, L., Larson, M.G.: The continuous Galerkin method is locally conservative. J. Comput. Phys. 163, 467–488 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  16. Iliev, O., Lazarov, R., Willems, J.: Variational multiscale finite element method for flows in highly porous media. Multiscale Model. Simul. 9, 1350–1372 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Kou, J., Sun, S.: Analysis of a combined mixed finite element and discontinuous Galerkin method for incompressible two-phase flow in porous media. Math. Methods Appl. Sci. 37, 962–982 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Lin, G., Liu, J., Mu, L., Ye, X.: Weak galerkin finite element methdos for darcy flow: anistropy and heterogeneity. J. Comput. Phys. 276, 422–437 (2014)

    Article  MathSciNet  Google Scholar 

  19. Lin, G., Liu, J., Sadre-Marandi, F.: A comparative study on the weak Galerkin, discontinuous Galerkin, and mixed finite element methods. J. Comput. Appl. Math. 273, 346–362 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. Liu, J., Cali, R.: A note on the approximation properties of the locally divergence-free finite elements. Int. J. Numer. Anal. Model. 5, 693–703 (2008)

    MathSciNet  MATH  Google Scholar 

  21. Raviart P.-A., Thomas, J. M.: A mixed finite element method for 2nd order elliptic problems. In: Mathematical Aspects of Finite Element Methods (Proc. Conf., Consiglio Naz. delle Ricerche (C.N.R.), Rome, 1975), Lecture Notes in Math., vol. 606, pp. 292–315. Springer, Berlin (1977)

  22. Riviere, B.: Discontinuous Galerkin methods for solving elliptic and parabolic equations: theory and implementation. SIAM, Philadelphia (2008)

    Book  Google Scholar 

  23. Sun, S., Liu, J.: A locally conservative finite element method based on piecewise constant enrichment of the continuous galerkin method. SIAM J. Sci. Comput. 31, 2528–2548 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Thomas, J. W.: Numerical Partial Differential Equations, Vol. 33 of Texts in Applied Mathematics. Springer, New York (1999). Conservation laws and elliptic equations

  25. Wang, H., Liang, D., Ewing, R., Lyons, S., Qin, G.: An approximation to miscible fluid flows in porous media with point sources and sinks by an Eulerian–Lagrangian localized adjoint method and mixed finite element methods. SIAM J. Sci. Comput. 22, 561–581 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, J., Ye, X.: A weak galerkin finite element method for second order elliptic problems. J. Comput. Appl. Math. 241, 103–115 (2013)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Wyoming, Laramie, WY, 82071, USA

    Victor Ginting

  2. Department of Mathematics, School of Mechanical Engineering, Purdue University, West Lafayette, IN, 47907, USA

    Guang Lin

  3. Department of Mathematics, Colorado State University, Fort Collins, CO, 80523-1874, USA

    Jiangguo Liu

Authors
  1. Victor Ginting
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guang Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jiangguo Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jiangguo Liu.

Additional information

V. Ginting was partially supported by US National Science Foundation under Grant DMS-1016283. G. Lin would like to acknowledge support by the Applied Mathematics program of the US DOE Office of Advanced Scientific Computing Research and Pacific Northwest National Laboratory’s Carbon Sequestration Initiative, which is part of the Laboratory Directed Research and Development Program. J. Liu was partially supported by US National Science Foundation under Grant DMS-1419077.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ginting, V., Lin, G. & Liu, J. On Application of the Weak Galerkin Finite Element Method to a Two-Phase Model for Subsurface Flow. J Sci Comput 66, 225–239 (2016). https://doi.org/10.1007/s10915-015-0021-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0021-8

Keywords

Mathematics Subject Classification