Skip to main content
Springer Nature Link
Log in

A Well-Balanced Stochastic Galerkin Method for Scalar Hyperbolic Balance Laws with Random Inputs

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

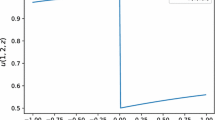
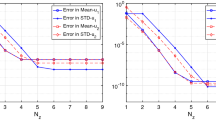
We propose a generalized polynomial chaos based stochastic Galerkin methods for scalar hyperbolic balance laws with random geometric source terms or random initial data. This method is well-balanced (WB), in the sense that it captures the stochastic steady state solution with high order accuracy. The framework of the stochastic WB schemes is presented in details, along with several numerical examples to illustrate their accuracy and effectiveness. The goal of this paper is to show that the stochastic WB scheme yields a more accurate numerical solution at steady state than the non-WB ones.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Bates, P., Lane, S., Ferguson, R.: Parametrization, validation and uncertainty analysis of CFD models of fluvial and flood hydraulics in natural enviroments. In: Computational Fluid Dynamics: Applications in Environmental Hydraulics. Wiley (2005)

  2. Bermudez, A., Vazquez, M.E.: Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 23(8), 1049–1071 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  3. Botchorishvili, R., Perthame, B., Vasseur, A.: Equilibrium schemes for scalar conservation laws with stiff sources. Math. Comput. 72(241), 131–157 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bouchut, F.: Nonlinear stability of finite volume methods for hyperbolic conservation laws and well-balanced schemes for sources. In: Frontiers in Mathematics. Birkhäuser Verlag, Basel (2004)

  5. Bürger, R., Kröker, I., Rohde, C.: A hybrid stochastic galerkin method for uncertainty quantification applied to a conservation law modelling a clarifier-thickener unit. Z. Angew. Math. Mech. 94(10), 793–817 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  6. Després, B., Poëtte, G., Lucor, D.: Robust uncertainty propagation in systems of conservation laws with the entropy closure method. In: Uncertainty Quantification in Computational Fluid Dynamics, pp. 105–149. Springer (2013)

  7. Fisher, P., Tate, N.: Causes and consequences of error in digitalk elevation models. Prog. Phys. Geogr. 30(4), 467–489 (2006)

    Article  Google Scholar 

  8. Fjordholm, U.S., Mishra, S., Tadmor, E.: Well-balanced and energy stable schemes for the shallow water equations with discontinuous topography. J. Comput. Phys. 230(14), 5587–5609 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ge, L., Cheung, K., Kobayashi, M.: Stochastic solution for uncertainty propagation in nonlinear shallow-water equations. J. Hydraul. Eng. 134(12), 1732–1743 (2008)

    Article  Google Scholar 

  10. Ghanem, R., Spanos, P.: Stochastic Finite Elements: A Spectral Approach. Springer, New York (1991)

    Book  MATH  Google Scholar 

  11. Godunov, S.: Finite difference schemes for numerical computation of solutions of the equations of fluid dynamics. Math. USSR Sb. 47, 271–306 (1959)

    MathSciNet  MATH  Google Scholar 

  12. Gosse, L.: A well-balanced flux-vector splitting scheme designed for hyperbolic systems of conservation laws with source terms. Comput. Math. Appl. 39(9–10), 135–159 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  13. Gosse, L., Leroux, A.-Y.: a well-balanced scheme designed for inhomogeneous scalar conservation laws. Comptes Rendus De L Academie Des Sciences Serie I-mathematique 323(5), 543–546 (1996)

    MathSciNet  MATH  Google Scholar 

  14. Greenberg, J.M., Leroux, A.-Y.: A well-balanced scheme for the numerical processing of source terms in hyperbolic equations. SIAM J. Numer. Anal. 33(1), 1–16 (1996)

    Article  MathSciNet  Google Scholar 

  15. Jin, S.: A steady-state capturing method for hyperbolic systems with geometrical source terms. ESAIM. Math. Model. Numer. Anal. 35(04), 631–645 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  16. LeVeque, R.J.: Balancing source terms and flux gradients in high-resolution Godunov methods: the quasi-steady wave-propagation algorithm. J. Comput. Phys. 146(1), 346–365 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, D.: Uncertainty Quantifications with Shallow Water Equations. Ph.D. thesis, TU Braunschweig and University of Florence (2009)

  18. Mishra, S., Schwab, C., Sukys, J.: Multi-level monte carlo finite volume methods for shallow water equations with uncertain topography in multi-dimensions. In: Technical Report 2011-70, Seminar for Applied Mathematics. ETH Zürich, Switzerland (2011)

  19. Perthame, B., Simeoni, C.: Convergence of the upwind interface source method for hyperbolic conservation laws. In: Hyperbolic Problems: Theory, Numerics, Applications, pp. 61–78. Springer (2003)

  20. Poëtte, G., Després, B., Lucor, D.: Uncertainty quantification for systems of conservation laws. J. Comput. Phys. 228(7), 2443–2467 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Roe, P.L.: Approximate riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 43(2), 357–372 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  22. Roe, P.L.: Upwind differenced schemes for hyperbolic conservation laws with source terms. In: Proceedings of the Conference Hyperbolic Problems, pp. 41–51 (1986)

  23. Tryoen, J., Matre, O.L., Ern, A.: Adaptive anisotropic spectral stochastic methods for uncertain scalar conservation laws. SIAM J. Sci. Comput. 34(5), A2459–A2481 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  24. Vázquez-Cendón, M.E.: Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry. J. Comput. Phys. 148(2), 497–526 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  25. Xing, Y., Shu, C.-W.: High order well-balanced finite volume weno schemes and discontinuous galerkin methods for a class of hyperbolic systems with source terms. J. Comput. Phys. 214(2), 567–598 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  26. Xiu, D.: Numerical Methods for Stochastic Computations. Princeton Univeristy Press, Princeton (2010)

    MATH  Google Scholar 

  27. Xiu, D., Karniadakis, G.: The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 24(2), 619–644 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  28. Xiu, D., Shen, J.: Efficient stochastic galerkin methods for random diffusion equations. J. Comput. Phys. 228(2), 266–281 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

S. Jin was partially supported by NSF DMS Grants Nos. 1107291 and 1107291: RNMS ”KI-Net”, and National Science Foundation of China Grant No. 91330203. D. Xiu was partially supported by AFOSR and DOE.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Wisconsin, Madison, WI, 53706, USA

    Shi Jin

  2. Department of Mathematics, Institute of Natural Sciences and MOE-LSC, Shanghai Jiao Tong University, Shanghai, 200240, China

    Shi Jin

  3. Scientific Computing and Imagining Institute and Department of Mathematics, University of Utah, Salt Lake City, UT, 84112, USA

    Dongbin Xiu

  4. Scientific Computing and Imaging Institute, University of Utah, Salt Lake City, UT, 84112, USA

    Xueyu Zhu

Authors
  1. Shi Jin
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dongbin Xiu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xueyu Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dongbin Xiu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jin, S., Xiu, D. & Zhu, X. A Well-Balanced Stochastic Galerkin Method for Scalar Hyperbolic Balance Laws with Random Inputs. J Sci Comput 67, 1198–1218 (2016). https://doi.org/10.1007/s10915-015-0124-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0124-2

Keywords