Abstract
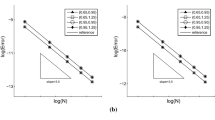
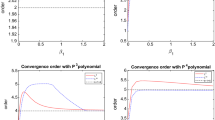
In this paper we introduce a hybridized discontinuous Galerkin (HDG) method for solving nonlinear Korteweg–de Vries type equations. Similar to a standard HDG implementation, we first express the approximate variables and numerical fluxes inside each element in terms of the approximate traces of the scalar variable (u), and its first derivative (\(u_x\)). These traces are assumed to be single-valued on each face. Next, we impose the conservation of numerical fluxes via two extra sets of equations. Using these global flux conservation conditions and applying the Newton–Raphson method, we construct a system of equations that can be solely expressed in terms of the increments of approximate traces in each iteration. Afterwards, we solve these equations, and substitute the approximate traces back into local equations over each element to obtain local approximate solutions. As for the time stepping scheme, we use the backward difference formulae. The method is proved to be stable for a proper choice of stabilization parameters. Through numerical examples, we observe that for a mesh with kth order elements, the computed u, p, and q show optimal convergence at order \(k+1\) in both linear and nonlinear cases, which improves upon previously employed techniques.


Similar content being viewed by others
References
Alexanderian, A., Petra, N., Stadler, G., Ghattas, O.: A fast and scalable method for a-optimal design of experiments for infinite-dimensional bayesian nonlinear inverse problems, p. 29 (2014)
Benzoni-Gavage, S., Danchin, R., Descombes, S., Jamet, D.: Structure of Korteweg models and stability of diffuse interfaces. Interfaces Free Bound. 7(4), 371–414 (2005)
Boffi, D., Brezzi, F., Fortin, M.: Mixed Finite Element Methods and Applications, vol. 44. Springer, Berlin (2013)
Braginskii, S.I.: Transport processes in a plasma. Rev. Plasma Phys. 1, 205 (1965)
Buckingham, M.: Theory of acoustic attenuation, dispersion, and pulse propagation in unconsolidated granular materials including marine sediments. J. Acoust. Soc. Am. 102(5, 1), 2579–2596 (1997)
Cockburn, B., Gopalakrishnan, J.: A characterization of hybridized mixed methods for second order elliptic problems. SIAM J. Numer. Anal. 42(1), 283–301 (2004)
Cockburn, B., Gopalakrishnan, J., Lazarov, R.: Unified hybridization of discontinuous galerkin, mixed, and continuous galerkin methods for second order elliptic problems. SIAM J. Numer. Anal. 47(2), 1319–1365 (2009)
Gardner, C.L.: The quantum hydrodynamic model for semiconductor devices. SIAM J. Appl. Math. 54(2), 409–427 (1994)
Heath, R.E., Gamba, I.M., Morrison, P.J., Michler, C.: A discontinuous Galerkin method for the Vlasov–Poisson system. J. Comput. Phys. 231(4), 1140–1174 (2012)
Holmer, J.: The initial-boundary value problem for the Korteweg–de Vries equation. Commun. Partial Differ. Equ. 31(8), 1151–1190 (2006)
Jain, A., Tamma, K.K.: Elliptic heat conduction specialized applications involving high gradients: local discontinuous galerkin finite element method—part 1. J. Therm. Stresses 33(4), 335–343 (2010)
Kaladze, T., Aburjania, G., Kharshiladze, O., Horton, W., Kim, Y.: Theory of magnetized Rossby waves in the ionospheric E layer. J. Geophys. Res. Space Phys
Kirby, R.M., Sherwin, S.J., Cockburn, B.: To CG or to HDG: a comparative study. J. Sci. Comput. 51(1), 183–212 (2012)
Kloeckner, A., Warburton, T., Bridge, J., Hesthaven, J.S.: Nodal discontinuous Galerkin methods on graphics processors. J. Comput. Phys. 228(21), 7863–7882 (2009)
Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. 39, 422–443 (1895)
Kostin, I., Marion, M., Texier-Picard, R., Volpert, V.: Modelling of miscible liquids with the Korteweg stress. ESAIM-Math. Modell. Numer. Anal. 37(5), 741–753 (2003)
Kubatko, E.J., Westerink, J.J., Dawson, C.: hp discontinuous Galerkin methods for advection dominated problems in shallow water flow. Comput. Methods Appl. Mech. Eng. 196(1–3), 437–451 (2006)
Larecki, W., Banach, Z.: Influence of nonlinearity of the phonon dispersion relation on wave velocities in the four-moment maximum entropy phonon hydrodynamics. Phys. D-Nonlinear Phenom. 266, 65–79 (2014)
Levy, D., Shu, C.-W., Yan, J.: Local discontinuous Galerkin methods for nonlinear dispersive equations. J. Comput. Phys. 196(2), 751–772 (2004)
Loverich, J., Hakim, A., Shumlak, U.: A discontinuous Galerkin method for ideal two-fluid plasma equations. Commun. Comput. Phys. 9(2), 240–268 (2011)
Michoski, C., Evans, J.A., Schmitz, P.G., Vasseur, A.: Quantum hydrodynamics with trajectories: the nonlinear conservation form mixed/discontinuous Galerkin method with applications in chemistry. J. Comput. Phys. 228(23), 8589–8608 (2009)
Michoski, C., Meyerson, D., Isaac, T., Waelbroeck, F.: Discontinuous galerkin methods for plasma physics in the scrape-off layer of tokamaks. J. Comput. Phys. 274, 898–919 (2014)
Nguyen, N.C., Peraire, J., Cockburn, B.: An implicit high-order hybridizable discontinuous galerkin method for nonlinear convection–diffusion equations. J. Comput. Phys. 228(23), 8841–8855 (2009)
Panda, N., Dawson, C., Zhang, Y., Kennedy, A.B., Westerink, J.J., Donahue, A.S.: Discontinuous Galerkin methods for solving Boussinesq–Green–Naghdi equations in resolving non-linear and dispersive surface water waves. J. Comput. Phys. 273, 572–588 (2014)
Peraire, J., Nguyen, N., Cockburn, B.: A hybridizable discontinuous Galerkin method for the compressible Euler and Navier–Stokes equations. AIAA Pap. 363, 2010 (2010)
Phillips, O.: Nonlinear dispersive waves. Annu. Rev. Fluid Mech. 6, 93–110 (1974)
Shukla, P.K., Eliasson, B.: Colloquium: nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 83(3), 885–906 (2011)
Tassi, E., Morrison, P.J., Waelbroeck, F.L., Grasso, D.: Hamiltonian formulation and analysis of a collisionless fluid reconnection model. Plasma Phys. Control. Fusion 50(8), 085014 (2008)
Woo, S.-B., Choi, Y.-K.: Development of finite volume model for KDV type equation. In: Zuo, Q.H., Dou, X.P., Ge, J.F., (Eds.), Asian and pacific coasts 2007, pp. 203–206, 2007. In: 4th International Conference on Asian and Pacific Coasts, Nanjing Hydraul Res Inst, Nanjing, Peoples Republic of China, Sept 21–24 (2007)
Yagi, M., Horton, W.: Reduced Braginskii equations. Phys. Plasmas 1(7), 2135–2139 (1994)
Yan, J., Shu, C.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002)
Yan, W., Liu, Z., Liang, Y.: Existence of solitary waves and periodic waves to a perturbed generalized KdV equation. Math. Model. Anal. 19(4), 537–555 (2014)
Zhang, Y., Kennedy, A.B., Panda, N., Dawson, C., Westerink, J.J.: Boussinesq–Green–Naghdi rotational water wave theory. Coast. Eng. 73, 13–27 (2013)
Acknowledgments
The authors would like to acknowledge the support of National Science Foundation Grant ACI 1339801. We also want to express our gratitude to the anonymous reviewers for their valuable comments to improve the quality of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors acknowledge the support of National Science Foundation Grant ACI 1339801.
Rights and permissions
About this article
Cite this article
Samii, A., Panda, N., Michoski, C. et al. A Hybridized Discontinuous Galerkin Method for the Nonlinear Korteweg–de Vries Equation. J Sci Comput 68, 191–212 (2016). https://doi.org/10.1007/s10915-015-0133-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-015-0133-1
Keywords
- Discontinuous Galerkin methods
- Nonlinear KdV equations
- Dispersive wave equation
- Hybrid mixed methods
- HDG