Penalty Method for the Stationary Navier–Stokes Problems Under the Slip Boundary Condition

Abstract

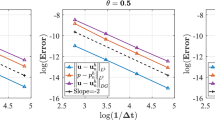
We consider the penalty method for the stationary Navier–Stokes equations with the slip boundary condition. The well-posedness and the regularity theorem of the penalty problem are investigated, and we obtain the optimal error estimate $O(\epsilon )$ in $H^k$-norm, where $\epsilon$ is the penalty parameter. We are concerned with the finite element approximation with the P1b / P1 element to the penalty problem. The well-posedness of discrete problem is proved. We obtain the error estimate $O(h+\sqrt{\epsilon }+h/\sqrt{\epsilon })$ for the non-reduced-integration scheme with $d=2,3$, and the reduced-integration scheme with $d=3$, where h is the discretization parameter and d is the spatial dimension. For the reduced-integration scheme with $d=2$, we prove the convergence order $O(h+\sqrt{\epsilon }+h^2/\sqrt{\epsilon })$. The theoretical results are verified by numerical experiments.

The Regularity for the Penalty Problem of the Stokes Equations

In this appendix we prove a regularity result for the Stokes equations subject to a penalized slip boundary condition. This is useful when we treat the nonlinearity in the Navier–Stokes equations as a perturbation term. We emphasize that the regularity estimate [see (6.2) below] is independent of the penalty coefficient $\epsilon ^{-1}$.

Theorem 6.1

For $k \in \mathbb {N} \cup \{0\}$, we assume $\varOmega$ is $C^{k+4}$ smooth and $f \in H^k(\varOmega )$, $g \in H^{k+ \frac{1}{2}}(\varGamma )$. Let $(u_\epsilon ,p_\epsilon ) \in V \times Q$ be the solution of the Stokes problem with penalty, denoted by $\mathbf{(S_\epsilon )}$:

$$\begin{aligned}&-\nu \varDelta u_\epsilon + \nabla p_\epsilon = f, \quad \nabla \cdot u_\epsilon = 0, \quad \text { in } \varOmega ,\end{aligned}$$

(6.1a)

$$\begin{aligned}&u_\epsilon |_C = 0, \quad \tau (u_\epsilon ,p_\epsilon ) + \epsilon ^{-1} u_{\epsilon n}n = g \quad \text { on } \varGamma . \end{aligned}$$

(6.1b)

Then we have

$$\begin{aligned} \Vert u_\epsilon \Vert _{H^{k+2}(\varOmega )} + \Vert p_\epsilon \Vert _{H^{k+1}(\varOmega )} \le C, \end{aligned}$$

(6.2)

where C is independent of penalty coefficient $\epsilon ^{-1}$.

The proof of Theorem 6.1 is based on the induction method. Firstly, we show the existence of the weak solution of (6.1). The weak form of (6.1) reads as

$$\begin{aligned} a(u_\epsilon ,v) + b(v,p_\epsilon ) + \frac{1}{\epsilon }\int _\varGamma u_{\epsilon n} v_n~d\varGamma&= (f,v) + \int _\varGamma g \cdot v~d\varGamma ,&\forall&v \in V, \end{aligned}$$

(6.3a)

$$\begin{aligned} b(u_\epsilon ,q)&= 0,&\forall&q \in Q. \end{aligned}$$

(6.3b)

Lemma 6.1

Given $f \in V'$ and $g \in H^{-\frac{1}{2}}(\varGamma )$, there exists a unique solution $(u_\epsilon .p_\epsilon ) \in V \times Q$ of (6.3), with

$$\begin{aligned} \Vert u_\epsilon \Vert _{H^1(\varOmega )} + \Vert p_\epsilon \Vert _{L^2(\varOmega )} + \epsilon ^{-\frac{1}{2}}\Vert u_{\epsilon n}\Vert _{L^2(\varGamma )} \le C\left( \Vert f\Vert _{V'} + \Vert g\Vert _{H^{-\frac{1}{2}}(\varGamma )}\right) . \end{aligned}$$

(6.4)

Proof

By Korn’s inequality and the Lax-Milgram theorem, there exists a unique solution $u_\epsilon$ of

$$\begin{aligned} a(u_\epsilon ,v) + \frac{1}{\epsilon }\int _\varGamma u_{\epsilon n} v_n~d\varGamma = (f,v) + \int _\varGamma g \cdot v~d\varGamma , \quad \forall v \in V^\sigma . \end{aligned}$$

(6.5)

with the estimate

$$\begin{aligned} \Vert u_\epsilon \Vert _{H^1(\varOmega )} + \epsilon ^{-\frac{1}{2}}\Vert u_{\epsilon n}\Vert _{L^2(\varGamma )} \le C\left( \Vert f\Vert _{V'} + \Vert g\Vert _{H^{-\frac{1}{2}}(\varGamma )}\right) \end{aligned}$$

(6.6)

By the inf-sup condition of b, there exists a unique $\mathring{p}_\epsilon \in \mathring{Q}$ satisfying

$$\begin{aligned}&a(u_\epsilon ,v) + b(v,\mathring{p}_\epsilon ) = (f,v), \quad \forall v \in H_0^1(\varOmega )^d, \end{aligned}$$

(6.7)

$$\begin{aligned}&\Vert \mathring{p}_\epsilon \Vert _{L^2(\varOmega )} \le C(\Vert u_\epsilon \Vert _{H^1(\varOmega )} + \Vert f\Vert _{V'}). \end{aligned}$$

(6.8)

For all $\phi \in C^\infty (\overline{\varOmega })^d \cap V$ with $\int _\varGamma \phi _nd\varGamma = 1$, we set

$$\begin{aligned} k_\epsilon = a(u_\epsilon ,\phi ) + b(\phi ,\mathring{p}_\epsilon ) + \epsilon ^{-1} \int _\varGamma u_{\epsilon n} \phi _n~d\varGamma - (f,\phi ) - \int _\varGamma g\cdot \phi ~d\varGamma . \end{aligned}$$

(6.9)

With a similar argument to Proposition 2.2, we see that $k_\epsilon$ is independent of $\phi$, and $(u_\epsilon ,p_\epsilon )$ with $p_\epsilon = \mathring{p}_\epsilon + k_\epsilon$ is a solution of (6.3).

Substituting $\phi = k_\epsilon \tilde{n}$ into (6.3), where $\tilde{n}$ is a smooth extension of $n \in C^3(\varGamma )$ to $\varOmega$, and noticing that $\int _\varGamma u_{\epsilon n} k_\epsilon n \cdot n d\varGamma = 0$, we obtain

$$\begin{aligned} \begin{aligned} |k_\epsilon |^2|\varGamma |&= -b(k_\epsilon \tilde{n},k_\epsilon ) \\&= a(u_\epsilon ,\phi ) + b(\phi ,\mathring{p}_\epsilon ) - (f,\phi ) - \int _\varGamma g\cdot \phi ~d\varGamma \\&\le C \left( \Vert u_\epsilon \Vert _{H^1(\varOmega )}+\Vert \mathring{p}_\epsilon \Vert _{L^2(\varOmega )} + \Vert f\Vert _{V'}+\Vert g\Vert _{H^{-\frac{1}{2}}(\varGamma )}\right) . \end{aligned} \end{aligned}$$

(6.10)

Combining (6.6), (6.8) and (6.10), we get (6.4). $\square$

Proof of Theorem 6.1

For any interior sub-domain $\omega \subset \varOmega$ or $\omega$ near the boundary $\gamma$, we have (cf. [8])

$$\begin{aligned} \Vert u_\epsilon \Vert _{H^{k+2}(\omega )} + \Vert p_\epsilon \Vert _{H^{k+1}(\omega )} \le C\Vert f\Vert _{H^k(\varOmega )}. \end{aligned}$$

We then consider the regularity near $\varGamma$. There exist $\{W_i\}_{i=1}^N \subset \mathbb {R}^d$ covering $\varGamma$, and $\{\theta _i\}_{i=1}^N$ with $\theta _i \subset C_0^\infty (W_i)$, $\theta _i \ge 0$, $\sum _{i=1}^N \theta _i = 1$, and $\text {supp }\theta _i \subsetneq W_i$. We will prove the $H^{k+2}$-regularity of $\theta _i u_\epsilon$ for every $W_i$, which implies (6.2). In the following, we omit the subscript i of $W_i$ and $\theta _i$. Setting $(\bar{u},\bar{p}) = (\theta u_\epsilon , \theta p_\epsilon )$ and $e_{ij}(u) = \frac{1}{2}(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i})$, we see that

$$\begin{aligned} e_{ij}(\bar{u}) = \theta e_{ij}(u_\epsilon ) + \frac{1}{2}\left( \frac{\partial \theta }{\partial x_j} u_{\epsilon i}+ \frac{\partial \theta }{\partial x_i}u_{\epsilon j}\right) , \quad \nabla \cdot (\theta v) = v \cdot \nabla \theta + \theta \nabla \cdot v. \end{aligned}$$

We re-set $V = H^1(W \cap \varOmega )^d \cap \{v|_{\partial (W \cap \varOmega ) \backslash \varGamma } = 0\}$, $Q = L^2(W \cap \varOmega )$, and re-define the bilinear forms $a(\cdot ,\cdot )$, $b(\cdot ,\cdot )$ in the domain $\varOmega \cap W$. From (6.3), we have (here and hereafter the summation convention is employed),

$$\begin{aligned}&\begin{aligned}&a(\bar{u},v) + b(v,\bar{p}) + \frac{1}{\epsilon }\int _{\varGamma \cap W} \bar{u}_n v_n d \varGamma \\&\quad = a(u_\epsilon ,\theta v) + b(\theta v,p_\epsilon ) + \frac{1}{\epsilon }\int _{\varGamma \cap W} u_{\epsilon n} \theta v_n d \varGamma + \nu \int _{\varOmega \cap W} o_{ij}(\theta ,u_\epsilon ) e_{ij}(v)dx \\&\qquad - \nu \int _{\varOmega \cap W} o_{ij}(\theta ,v) e_{ij}(u_\epsilon )dx + \int _{\varOmega \cap W} v \cdot \nabla \theta p_\epsilon ~dx\\&\quad = (\theta f + \nabla \theta p_\epsilon , v)_{W \cap \varOmega } + \nu (o_{ij}(\theta ,u_\epsilon ), e_{ij}(v))_{W \cap \varOmega } \\&\qquad + \nu (o_{ij}(\theta ,v), e_{ij}(u_\epsilon ))_{W \cap \varOmega } + \int _{\varGamma \cap W} \theta g \cdot v~d\varGamma , \quad \forall v \in V, \end{aligned} \end{aligned}$$

(6.11a)

$$\begin{aligned}&b(\bar{u},q) = -(u_\epsilon \cdot \nabla \theta ,q)_{\varOmega \cap W}, \quad \forall q \in L^2(W \cap \varOmega ), \end{aligned}$$

(6.11b)

where $o_{ij}(\theta ,u) = \frac{\partial \theta }{\partial x_j} u_i + \frac{\partial \theta }{\partial x_i} u_j$. With integration by parts, we obtain

$$\begin{aligned}&-\nabla \cdot \sigma (\bar{u}, \bar{p}) = \bar{f}, \quad \nabla \cdot \bar{u} = \bar{h} , \quad \text { in } W \cap \varOmega , \end{aligned}$$

(6.12a)

$$\begin{aligned}&\bar{u} = 0, \quad \text { on } \partial (W \cap \varOmega )\backslash \overline{\varGamma }, \quad \tau (\bar{u}, \bar{p}) + \epsilon ^{-1}\bar{u}_n n = \bar{g} \quad \text { on } \partial (W \cap \varOmega ) \cap \varGamma , \end{aligned}$$

(6.12b)

where

$$\begin{aligned}&\bar{f} = \theta f + \nabla \theta p_\epsilon - \nu ((u_\epsilon \cdot \nabla )\nabla \theta + 2 (\nabla \theta \cdot \nabla )u_\epsilon + \varDelta \theta u_\epsilon + \nabla u_\epsilon \nabla \theta ),\\&\bar{g} = \theta g - \nu ( u_{\epsilon n} \nabla \theta + (\nabla \theta \cdot n)u_\epsilon ), \quad \bar{h} = u_\epsilon \cdot \nabla \theta . \end{aligned}$$

There exists a $C^{k+3}$-diffeomorphism $\varvec{\Phi }$ (cf. [19, Proof of Lemma 4.1], [24] ), such that $0 < c \le |\text {Jac }\varvec{\Phi }| \le C$, $|\text {Jac }\varvec{\Phi }||\text {Jac }\varvec{\Phi }^{-1}| = 1$, and

• (1) $\varvec{\Phi }(W \cap \varOmega ) = Q_R := \{y = (y',y_d) \in \mathbb {R}^{d-1} \times \mathbb {R} : |y'|<R, \ 0 < y_d < R\}$;

• (2) $\varvec{\Phi }(W \cap \varGamma ) = S_R := \{y = (y',y_d) \in \mathbb {R}^{d-1} \times \mathbb {R} : |y'|<R, \ y_d =0\}$;

• (3) $\frac{\partial \varPhi _d}{\partial x_j} = \frac{\partial \varPhi _j}{\partial x_d} = 0, \quad \frac{\partial \varPhi _d}{\partial x_d} = -1, \text { on } W \cap \varGamma \ (j = 1,\ldots ,d-1)$;

• (4) $\varvec{\Phi } : n(x) \mapsto \tilde{n}(y) = (0,\ldots ,0,-1) \text { for } x \in W \cap \varGamma .$

Here, the $C^{k+4}$-smoothness of $\varGamma$ is sufficient to obtain (3) and (4) (cf. [24, §1.2.4, Theorem 2.12]).

We set $y = \varvec{\Phi }(x) = (\varPhi _1(x), \ldots , \varPhi _d(x))$, and

$$\begin{aligned}&\tilde{U}(y) = \bar{u}(x), \quad \tilde{P}(y) = \bar{p}(x),\\&\tilde{F}(y) = \bar{f}(x) |\text {Jac }\varvec{\Phi }|, \quad \tilde{G}(y) = (\theta g)(x) \sqrt{\mathrm {det}\,A} , \quad \tilde{H}(y) = \bar{h}(x) |\text {Jac }\varvec{\Phi }|,\\&\tilde{u}_\epsilon (y) = u_\epsilon (x), \quad \tilde{p}_\epsilon (y) = p_\epsilon (x), \quad \tilde{\theta }(y) = \theta (x), \end{aligned}$$

where A is a $(d-1)\times (d-1)$ matrix, whose components are given by $A_{ij} = \frac{\partial \varvec{\Phi }^{-1}}{\partial y_i}\cdot \frac{\partial \varvec{\Phi }^{-1}}{\partial y_j}.$ Under the assumption of $k=0$ and (6.4), we see that

$$\begin{aligned} \Vert \tilde{F}\Vert _{L^2(Q_R)} + \Vert \tilde{G}\Vert _{H^\frac{1}{2}(S_R)} + \Vert \tilde{H}\Vert _{H^1(Q_R)} \le C. \end{aligned}$$

We introduce $K(Q_R) = \{ \varphi \in H^1(Q_R)^d : \varphi (y) = 0 \text { for } |y'| = R, \ y_d = R\}.$ Then $(\tilde{U},\tilde{P})$ satisfies

$$\begin{aligned}&\begin{aligned} \tilde{a}(\tilde{U},\tilde{\varphi }) +&\tilde{b}(\tilde{\varphi },\tilde{P}) + \frac{1}{\epsilon }\int _{S_R} \tilde{U}_d \tilde{\varphi }_d \sqrt{\mathrm {det}\,A} ~dy' \\ =&(\tilde{F}, \tilde{\varphi })_{Q_R} + \int _{S_R} \tilde{G}\cdot \tilde{\varphi } ~dy', \quad \forall \tilde{\varphi } \in K(Q_R), \end{aligned} \end{aligned}$$

(6.13a)

$$\begin{aligned}&\tilde{b}(\tilde{U},\tilde{q}) = (\tilde{H}, \tilde{q})_{Q_R}, \quad \forall \tilde{q} \in L^2(Q_R). \end{aligned}$$

(6.13b)

Here we have put

$$\begin{aligned}&\tilde{a}(\tilde{U},\tilde{\varphi }) = 2\nu \int _{Q_R} \tilde{e}_{ij}(\tilde{U}) \tilde{e}_{ij}(\tilde{\varphi })|\text {Jac } \varvec{\Phi } |~dy, \quad \tilde{e}_{ij}(\tilde{U}) = \frac{1}{2}\left( \frac{\partial \varPhi _k}{\partial x_j} \frac{\partial \tilde{U}_i}{\partial y_k} + \frac{\partial \varPhi _k}{\partial x_i} \frac{\partial \tilde{U}_j}{\partial y_k}\right) ;\nonumber \\ \end{aligned}$$

(6.14)

$$\begin{aligned}&\tilde{b}(\tilde{U},\tilde{q}) = - \int _{Q_R} \tilde{q} \frac{\partial \varPhi _k}{\partial x_j} \frac{\partial \tilde{U}_j}{\partial y_k} |\text {Jac } \varvec{\Phi } |~dy. \end{aligned}$$

(6.15)

Now we consider the case of $k=0$. According the smoothness assumption on the data, we have $\Vert \tilde{F}\Vert _{L^2(Q_R)} + \Vert \tilde{G}\Vert _{H^\frac{1}{2}(S_R)} \le C$. Substituting $\tilde{\varphi } = \tilde{U}$ into (6.13) and using Korn’s inequality $\tilde{a}(\cdot ,\cdot ) \ge \tilde{\alpha }_1 \Vert \cdot \Vert _{H^1(Q_R)}^2$, we obtain

$$\begin{aligned} \Vert \tilde{U}\Vert _{H^1(Q_R)}^2 + \epsilon ^{-1}\Vert \tilde{U}_d\Vert _{L^2(S_R)}^2 \le C. \end{aligned}$$

(6.16)

For $\zeta > 0$, and $v \in K(Q_R)$, we introduce a difference quotient operator $D_\zeta ^i$ by

$$\begin{aligned} v(x_i+\zeta ) = v(x_1,\cdots ,x_i+\zeta ,\cdots ,x_d), \quad D_\zeta ^i v = (v(x_i+\zeta )-v(x))/\zeta . \end{aligned}$$

The following facts are well known:

$$\begin{aligned}&(w,D_{-\zeta }^i v) = (D_\zeta ^i w,v), \quad \Vert D_\zeta ^i w\Vert _{L^p(Q_R)} \le C \Vert \nabla _{y_i} w \Vert _{L^p(Q_R)}, \quad p \in (1,\infty ), \end{aligned}$$

(6.17)

$$\begin{aligned}&D_\zeta ^i(w(x)v(x)) = (D_\zeta ^i w) v(x_i+\zeta ) + w(x) (D_\zeta ^i v) ,\quad \forall w,v \in K(Q_R). \end{aligned}$$

(6.18)

Substituting $\tilde{\varphi } = D_{-\zeta }^i D_\zeta ^i \tilde{U}$ ($i = 1, \ldots ,d-1$) into (6.13) and using the above facts, together with Sobolev’s and Poincaré’s inequalities, we have the following five estimates:

$$\begin{aligned}&\begin{aligned} |(\tilde{F} ,D_{-\zeta }^i D_\zeta ^i \tilde{U})_{Q_R} | \le C\Vert D_{-\zeta }^i D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)}, \end{aligned} \end{aligned}$$

(6.19)

$$\begin{aligned}&\begin{aligned} \left| \int _{S_R} \tilde{G}\cdot \left( D_{-\zeta }^i D_\zeta ^i \tilde{U}\right) ~dy'\right|&\le C\left( \Vert D_\zeta ^i \tilde{G} \Vert _{H^{-\frac{1}{2}}(S_R)} + \Vert \tilde{G} \Vert _{H^{-\frac{1}{2}}(S_R)}\right) \Vert D_\zeta ^i \tilde{U}\Vert _{H^\frac{1}{2}(S_R)}\\&\le C \Vert \tilde{G} \Vert _{H^\frac{1}{2}(S_R)} \Vert D_\zeta ^i \tilde{U}\Vert _{H^1(Q_R)} \quad (\text {cf. [19, Lemma 6.1]})\\&\le C \Vert \nabla D_\zeta ^i \tilde{U} \Vert _{L^2(Q_R)}, \\ \end{aligned} \end{aligned}$$

(6.20)

$$\begin{aligned}&\begin{aligned}&\tilde{a}\left( \tilde{U}, D_{-\zeta }^i D_\zeta ^i \tilde{U}\right) \ge \tilde{a}\left( D_\zeta ^i \tilde{U},D_\zeta ^i \tilde{U}\right) - C_2\Vert \tilde{u}_\epsilon \Vert _{H^1(Q_R)} \Vert \nabla D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)} \\&\qquad \ge C_1 \Vert \nabla D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)} ^2 - C_2\Vert \tilde{u}_\epsilon \Vert _{H^1(Q_R)} \Vert \nabla D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)} \quad (\text {cf. [19, (4.17)]}), \end{aligned} \end{aligned}$$

(6.21)

$$\begin{aligned}&\begin{aligned} \frac{1}{\epsilon }\int _{S_R} \tilde{U}_d \left( D_{-\zeta }^i D_\zeta ^i \tilde{U}_d\right) \sqrt{\mathrm {det}\,A}~dy'&\ge C_3\frac{1}{\epsilon }\int _{S_R} |D_\zeta ^i \tilde{U}_{d}|^2 ~dy' - C_4 \frac{1}{\epsilon } \int _{S_R} |D_\zeta ^i \tilde{U}_{d}| |\tilde{U}_d|~dy'\\&\ge C_5\epsilon ^{-1}\Vert D_\zeta ^i \tilde{U}_{d}\Vert ^2_{L^2(S_R)} - C \quad (\text {by (6.16)}), \end{aligned} \end{aligned}$$

(6.22)

$$\begin{aligned}&\begin{aligned}&|\tilde{b}\left( D_{-\zeta }^i D_\zeta ^i \tilde{U},\tilde{P}\right) | = \left| \left( \frac{\partial \tilde{U}_j}{\partial y_k}, D_{\zeta }^i D_{-\zeta }^i \left( \tilde{P} \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } | \right) \right) _{Q_R} \right| \\&\qquad = \left| \left( \tilde{H}, \left( \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } |\right) ^{-1} D_{\zeta }^i D_{-\zeta }^i \left( \tilde{P} \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } | \right) \right) _{Q_R} \right| \quad (\text {by (6.13b)}) \\&\qquad \le C\left( \Vert \nabla D_\zeta ^i \tilde{H}\Vert _{L^2(Q_R)} + \Vert \tilde{H}\Vert _{H^1(Q_R)}\right) \Vert \tilde{P}\Vert _{L^2(Q_R)} \\&\qquad \le C \Vert \nabla D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)} \quad (\text {by } \tilde{H}(y) = (u_\epsilon \cdot \nabla \theta )(x)). \end{aligned} \end{aligned}$$

(6.23)

Combining (6.19)–(6.23), we conclude, for all $i = 1,\ldots ,d-1$,

$$\begin{aligned} \Vert \nabla D_\zeta ^i \tilde{U}\Vert _{L^2(Q_R)}^2 + \epsilon ^{-1} \Vert D_\zeta ^i \tilde{U}_{d}\Vert ^2_{L^2(S_R)} \le C, \end{aligned}$$

(6.24)

which implies (passing to the limit $\zeta \rightarrow 0$), for all $j = 1,\ldots ,d$ and $i = 1,\ldots ,d-1$,

$$\begin{aligned} \Vert \nabla _{y_j} \nabla _{y_i} \tilde{U}\Vert _{L^2(Q_R)}^2 + \epsilon ^{-1} \Vert \nabla _{y_i} \tilde{U}_{d}\Vert ^2_{L^2(S_R)} \le C. \end{aligned}$$

(6.25)

From (6.25) and the strong from of (6.13) (which can be obtained by the integration by parts), we have

$$\begin{aligned} \Vert \nabla _{y_d} \nabla _{y_d} \tilde{U}\Vert _{L^2(Q_R)} \le C\Vert \tilde{F}\Vert _{L^2(Q_R)} + C \sum _{i+j \le 2d-1}\Vert \nabla _{y_j} \nabla _{y_i} \tilde{U}\Vert _{L^2(Q_R)} \le C . \end{aligned}$$

(6.26)

Hence, we have proved the case of $k=0$. As a result of (6.12b), we have

$$\begin{aligned} \Vert u_{\epsilon n}\Vert _{H^\frac{1}{2}(\varGamma )} \le C\epsilon . \end{aligned}$$

(6.27)

Let us show the case of $k=1$, which is equivalent to prove $\Vert \nabla _{y_l} \tilde{U}\Vert _{H^2}\le C$, for $l = 1,\ldots ,d$. First, we calculate the equation of $\nabla _{y_l} \tilde{U}$, for $l = 1,\ldots ,d-1$. Since $\text {supp } \theta \subsetneq W$, compact, we have

$$\begin{aligned} \text {supp } \tilde{U} \subsetneq W, \text { compact }; \quad \text {supp } D_\zeta ^l \tilde{U} \subsetneq W, \text { compact, for all } l = 1,\ldots , d-1. \end{aligned}$$

Therefore, for any $\tilde{v} \in K(Q_R)$, $\tilde{q}_1 \in L^2(Q_R)$, we can substitute $\tilde{\varphi } = D_{-\zeta }^l \tilde{v}$, $\tilde{q} = D_{-\zeta }^l \tilde{q}_1$ into (6.13) (here, $\tilde{q}_1$ and $\tilde{v}$ are extended to $\mathbb {R}^{d-1} \times (0,R)$ by zero). Then, applying (6.17), (6.18), and passing to the limit $\zeta \rightarrow 0$, we obtain

$$\begin{aligned}&\begin{aligned}&\tilde{a}\left( \nabla _{y_l} \tilde{U},\tilde{v}\right) + \tilde{b}\left( \tilde{v},\nabla _{y_l} \tilde{P}\right) + \frac{1}{\epsilon }\int _{S_R} \left( \nabla _{y_l} \tilde{U}_d\right) \tilde{v}_d \sqrt{\mathrm {det}\,A} ~dy' \\&\quad = \left( \tilde{J}_l,\tilde{v}\right) _{Q_R} + \int _{S_R} \tilde{L}_l \cdot \tilde{v}~dy' - \frac{1}{\epsilon }\int _{S_R} \tilde{U}_d \tilde{v}_d \nabla _{y_l} \sqrt{\mathrm {det}\,A} ~dy', \quad \forall \tilde{v} \in K(Q_R), \end{aligned} \end{aligned}$$

(6.28a)

$$\begin{aligned}&\tilde{b}(\nabla _{y_l} \tilde{U},\tilde{q}_1) = (\tilde{H}_l ,\tilde{q}_1)_{Q_R}, \quad \forall \tilde{q}_1 \in L^2(Q_R), \end{aligned}$$

(6.28b)

where

$$\begin{aligned}&\tilde{J}_l = d_{1l} \frac{\partial \tilde{F} }{\partial y_l} + d_{2l} \frac{\partial \tilde{P} }{\partial y_l} + d_{3lik} \frac{\partial ^2 \tilde{U}_{i} }{\partial y_l \partial y_k} + d_{4li}\frac{\partial \tilde{U}_{i}}{\partial y_l} + d_{5l} \tilde{P} + d_{6l}\tilde{F}, \end{aligned}$$

(6.29)

$$\begin{aligned}&\tilde{L}_l = d_{7l} \frac{\partial \tilde{G} }{\partial y_l} + d_{8l} \tilde{G}, \end{aligned}$$

(6.30)

$$\begin{aligned}&\tilde{H}_l = d_{9li} \frac{\partial \tilde{U}_i }{\partial y_l} + d_{10l} \tilde{U}_{l}. \end{aligned}$$

(6.31)

Here $d_{sl}, d_{sli}, d_{slik} \in C^{k+1}(Q_R)$ (or $C^{k+1}(Q_R)^d$) for any $s=1,\ldots , 10$ and $1\le i,k\le d$, which are composed of $\tilde{\theta }$, $\frac{\partial \tilde{\theta } }{\partial y_k}$, $\frac{\partial ^2 \tilde{\theta } }{\partial y_k \partial y_l}$, $\varvec{\Phi }$, $|\text {Jac } \varvec{\Phi }|$, $\frac{\partial \varPhi _k }{\partial x_i}$, $\frac{\partial ^2 \varPhi _k }{\partial x_i \partial x_j}$, and $\frac{\partial |\text {Jac } \varvec{\Phi }| }{\partial x_i}$.

With the assumption of $k=1$ and the regularity results of $k=0$, we see that

$$\begin{aligned} \Vert f\Vert _{H^1(\varOmega )} + \Vert g\Vert _{H^\frac{3}{2}(\varGamma )} + \Vert u_\epsilon \Vert _{H^2(\varOmega )} + \Vert p_\epsilon \Vert _{H^1(\varOmega )} \le C, \end{aligned}$$

which implies

$$\begin{aligned} \Vert \tilde{J}_l\Vert _{L^2(Q_R)} + \Vert \tilde{L}_l\Vert _{H^\frac{1}{2}(S_R)} + \Vert \tilde{H}_l\Vert _{H^1(Q_R)} \le C. \end{aligned}$$

Now, substituting $\tilde{v} = \nabla _{y_l} \tilde{U}$ into (6.28) and using $\epsilon ^{-1} \Vert \tilde{U}_d\Vert _{L^2(\varGamma )} \le C$ obtained from (6.27), we get:

$$\begin{aligned} \left\| \nabla \frac{\partial \tilde{U}}{\partial y_l} \right\| _{L^2(Q_R)}^2 + \epsilon ^{-1} \left\| \frac{\partial \tilde{U}_d}{\partial y_l} \right\| _{L^2(S_R)}^2 \le C, \quad \forall l = 1,\ldots ,d-1. \end{aligned}$$

(6.32)

Substituting $\tilde{v} = D_{-\zeta }^i D_\zeta ^i \nabla _{y_l}\tilde{U}$ ($i = 1, \ldots ,d-1$) into (6.28) and using (6.17), (6.18) together with the Sobolev inequality, we have the following six estimates:

$$\begin{aligned}&\begin{aligned} \left| \left( \tilde{J}_l,D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}\right) _{Q_R}\right| \le C\Vert D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)}, \end{aligned} \end{aligned}$$

(6.33)

$$\begin{aligned}&\begin{aligned}&\left| \int _{S_R}\tilde{L}_l \cdot (D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U})~dy'\right| \\&\qquad \le C \Vert D_\zeta ^i \tilde{L}_l \Vert _{H^{-\frac{1}{2}}(S_R)} \Vert D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{H^\frac{1}{2}(S_R)} \\&\qquad \le C \Vert \tilde{L}_l \Vert _{H^\frac{1}{2}(S_R)} \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)} \le C \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)} , \end{aligned} \end{aligned}$$

(6.34)

$$\begin{aligned}&\begin{aligned}&\tilde{a}(\nabla _{y_l} \tilde{U}_l,D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}) \\&\qquad \ge C_1 \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)} ^2 - C_2\Vert \nabla _{y_l} \tilde{u}_\epsilon \Vert _{H^1(Q_R)} \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)} , \end{aligned} \end{aligned}$$

(6.35)

$$\begin{aligned}&\begin{aligned}&| \tilde{b}(D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}, \nabla _{y_l} \tilde{P}) | = \left| \left( \frac{\partial (\nabla _{y_l} \tilde{U}_j)}{\partial y_k}, D_{\zeta }^i D_{-\zeta }^i \left( \nabla _{y_l} \tilde{P} \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } | \right) \right) _{Q_R} \right| \\&\qquad = \left| \left( \tilde{H}_l, \left( \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } |\right) ^{-1} D_{\zeta }^i D_{-\zeta }^i \left( \nabla _{y_l} \tilde{P} \frac{\partial \varPhi _k}{\partial x_j} |\text {Jac } \varvec{\Phi } | \right) \right) _{Q_R} \right| \quad (\text {by (6.28b)} ) \\&\qquad \le C(\Vert \nabla D_\zeta ^i \tilde{H}_l\Vert _{L^2(Q_R)} + \Vert \tilde{H}_l\Vert _{H^1(Q_R)}) \Vert \nabla _{y_l} \tilde{P}\Vert _{L^2(Q_R)} \\&\qquad \le C \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)} \quad (\text {by } (6.31)), \end{aligned} \end{aligned}$$

(6.36)

$$\begin{aligned}&\begin{aligned}&\frac{1}{\epsilon }\int _{S_R} \nabla _{y_l} \tilde{U}_d (D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}_d) \sqrt{\mathrm {det}\,A} ~dy' \\&\qquad \ge C_3\frac{1}{\epsilon }\int _{S_R} |D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}|^2 ~dy' - C_4 \frac{1}{\epsilon } \int _{S_R} |D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}| |\nabla _{y_l} \tilde{U}_d|~dy'\\&\qquad \ge C_5\epsilon ^{-1}\Vert D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}\Vert ^2_{L^2(S_R)} - C \quad (\text {by (6.32)}) , \end{aligned} \end{aligned}$$

(6.37)

$$\begin{aligned}&\begin{aligned}&\left| \frac{1}{\epsilon }\int _{S_R} \tilde{U}_d (D_{-\zeta }^i D_\zeta ^i \nabla _{y_l} \tilde{U}_d) \nabla _{y_l} \sqrt{\mathrm {det}\,A} ~dy'\right| \\&\qquad \le C_6 \epsilon ^{-1} (\Vert D_{\zeta }^i \tilde{U}_d \Vert _{L^2(S_R)} + \Vert \tilde{U}_d \Vert _{L^2(S_R)} )\Vert D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}\Vert _{L^2(S_R)} \\&\qquad \le \frac{C_5}{2\epsilon } \Vert D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}\Vert _{L^2(S_R)}^2 + C_7 \quad (\text {by (6.27) and (6.32)}). \end{aligned} \end{aligned}$$

(6.38)

Combining (6.33)–(6.38), we conclude

$$\begin{aligned} \Vert \nabla D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}\Vert _{L^2(Q_R)}^2 + \epsilon ^{-1} \Vert D_\zeta ^i \nabla _{y_l} \tilde{U}_{d}\Vert _{L^2(S_R)}^2 \le C, \quad \forall i = 1,\ldots ,d-1, \end{aligned}$$

(6.39)

which yields (passing to the limit $\zeta \rightarrow 0$):

$$\begin{aligned} \Vert \nabla \nabla _{y_i} \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)}^2 + \epsilon ^{-1} \Vert \nabla _{y_i} \nabla _{y_l} \tilde{U}_{d}\Vert _{L^2(S_R)}^2 \le C, \quad \forall i = 1,\ldots ,d-1. \end{aligned}$$

(6.40)

From (6.40) and the equation of $(\nabla _{y_l}\tilde{U},\nabla _{y_l}\tilde{P})$ (the strong from of (6.28), which can be obtained by the integration by parts), we obtain

$$\begin{aligned} \Vert \nabla _{y_d} \nabla _{y_d} \nabla _{y_l} \tilde{U}\Vert _{L^2(Q_R)}^2 \le C. \end{aligned}$$

(6.41)

Since we have (6.40) and (6.41) for all $l = 1,\ldots ,d-1$, from the equation of $(\tilde{U},\tilde{P})$ (the strong from of (6.13), which can be obtained by the integration by parts), we conclude

$$\begin{aligned} \Vert \nabla _{y_d} \nabla _{y_d} \tilde{U}\Vert _{H^1(Q_R)} \le C\Vert \tilde{F}\Vert _{H^1(Q_R)} + C \sum _{j+i \le 2d-1} \Vert \nabla _{y_j} \nabla _{y_i} \tilde{U}\Vert _{H^1(Q_R)} \le C. \end{aligned}$$

(6.42)

Hence, we show the case of $k=1$ for (6.2). For $k \ge 2$, it follows from the induction method. $\square$