Skip to main content
SpringerLink
Log in

A Spectral Element Method with Transparent Boundary Condition for Periodic Layered Media Scattering

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

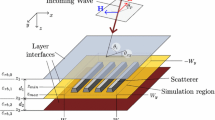
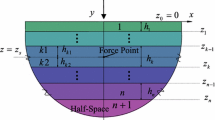
We present a high-order spectral element method for solving layered media scattering problems featuring an operator that can be used to transparently enforce the far-field boundary condition. The incorporation of this Dirichlet-to-Neumann (DtN) map into the spectral element framework is a novel aspect of this work, and the resulting method can accommodate plane-wave radiation of arbitrary angle of incidence. In order to achieve this, the governing Helmholtz equations subject to quasi-periodic boundary conditions are rewritten in terms of periodic unknowns. We construct a spectral element operator to approximate the DtN map, thus ensuring nonreflecting outgoing waves on the artificial boundaries introduced to truncate the computational domain. We present an explicit formula that accurately computes the Fourier coefficients of the solution in the spectral element discretization space projected onto the boundary which is required by the DtN map. Our solutions are represented by the tensor product basis of one-dimensional Legendre–Lagrange interpolation polynomials based on the Gauss–Lobatto–Legendre grids. We study the scattered field in singly and doubly layered media with smooth and nonsmooth interfaces. We consider rectangular, triangular, and sawtooth interfaces that are accurately represented by the body-fitted quadrilateral elements. We use GMRES iteration to solve the resulting linear system, and we validate our results by demonstrating spectral convergence in comparison with exact solutions and the results of an alternative computational method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Banerjee, P.K., Butterfield, R.: Boundary element methods in engineering science. McGraw-Hill, London (1981)

    MATH  Google Scholar 

  2. Bonnet, M.: Boundary integral equation methods for solids and fluids. Wiley, New Jersey (1999)

    Google Scholar 

  3. Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  4. Bruno, O.P., Reitich, F.: Numerical solution of diffraction problems: a method of variation of boundaries. J. Opt. Soc. Am. A 10(6), 1168–1175 (1993)

    Article  Google Scholar 

  5. Bruno, O.P., Reitich, F.: Numerical solution of diffraction problems: a method of variation of boundaries. II. Finitely conducting gratings, Padé approximants, and singularities. J. Opt. Soc. Am. A 10(11), 2307–2316 (1993)

    Article  Google Scholar 

  6. Bruno, O.P., Reitich, F.: Numerical solution of diffraction problems: a method of variation of boundaries. III. Doubly periodic gratings. J. Opt. Soc. Am. A 10(12), 2551–2562 (1993)

    Article  Google Scholar 

  7. Milder, D.M.: An improved formalism for rough-surface scattering of acoustic and electromagnetic waves. In: Proceedings of SPIE—the international society for optical engineering (San Diego, 1991), 1558, pp. 213–221. Bellingham, WA (1991)

  8. Milder, D.M.: An improved formalism for wave scattering from rough surfaces. J. Acoust. Soc. Am. 89(2), 529–541 (1991)

    Article  Google Scholar 

  9. Milder, D.M.: Role of the admittance operator in rough-surface scattering. J. Acoust. Soc. Am. 100(2), 759–768 (1996)

    Article  Google Scholar 

  10. Milder, D.M.: An improved formalism for electromagnetic scattering from a perfectly conducting rough surface. Radio Sci. 31(6), 1369–1376 (1996)

    Article  Google Scholar 

  11. Milder, D.M., Sharp, H.: Efficient computation of rough surface scattering. In: Mathematical and numerical aspects of wave propagation phenomena (Strasbourg, 1991), pp. 314–322, SIAM, Philadelphia, PA (1991)

  12. Milder, D.M., Sharp, H.T.: An improved formalism for rough surface scattering. II: numerical trials in three dimensions. J. Acoust. Soc. Am. 91(5), 2620–2626 (1992)

    Article  Google Scholar 

  13. Nicholls, D.P., Shen, J.: A rigorous numerical analysis of the transformed field expansion method. SIAM J. Numer. Anal. 47(4), 2708–2734 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Nicholls, D.P., Shen, J.: A stable, high-order method for two-dimensional bounded-obstacle scattering. SIAM J. Sci. Comput. 28(4), 1398–1419 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  15. Fang, Q., Nicholls, D.P., Shen, J.: A stable, high-order method for three-dimensional bounded-obstacle scattering. J. Comput. Phys. 224(2), 1145–1169 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  16. Petit, R.: Electromagnetic theory of gratings. Springer, Berlin (1980)

    Book  Google Scholar 

  17. Nicholls, D.P., Reitich, F.: A new approach toanalyticity of Dirichlet–Neumann operators. Proc. R. Soc. Edinb. Sect. A. Math. 131(6), 1411–1433 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  18. Nicholls, D.P., Reitich, F.: Stability of high-order perturbative methods for the computation of Dirichlet-Neumann operators. J. Comput. Phys. 170(1), 276–298 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  19. Nicholls, D.P., Reitich, F.: Analytic continuation of Dirichlet-Neumann operators. Numer. Math. 94(1), 107–146 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  20. He, Y., Nicholls, D.P., Shen, J.: An efficient and stable spectral method for electromagnetic scattering from a layered periodic structure. J. Comput. Phys. 231(8), 3007–3022 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Nicholls, D.P.: A method of field expansions for vector electromagnetic scattering by layered periodic crossed gratings. J. Opt. Soc. Am. A 32(5), 701–709 (2015)

    Article  Google Scholar 

  22. Deville, M.O., Fischer, P.F., Mund, E.H.: High-order methods for incompressible fluid flow. Cambridge University Press, Cambridge (2002)

    Book  MATH  Google Scholar 

  23. Han, H.D., Wu, X.N.: Approximation of infinite boundary condition and its application to finite element methods. J. Comput. Math. 3(2), 179–192 (1985)

    MathSciNet  MATH  Google Scholar 

  24. Keller, J., Givoli, D.: Exact nonreflecting boundary conditions. J. Comput. Phys. 82(1), 172–192 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  25. Givoli, D.: Nonreflecting boundary conditions. J. Comput. Phys. 94(1), 1–29 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  26. Givoli, D., Keller, J.: Special finite elements for use with high-order boundary conditions. Comput. Methods Appl. Mech. Eng. 119(3–4), 199–213 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  27. Givoli, D.: Numerical methods for problems in infinite domains. Elsevier Scientific Publishing Co., Amsterdam (1992)

    MATH  Google Scholar 

  28. Grote, M., Keller, J.: On nonreflecting boundary conditions. J. Comput. Phys. 122(2), 231–243 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  29. Givoli, D.: Recent advances in the DtN FE method. Arch. Comput. Methods Eng. 6(2), 71–116 (1999)

    Article  MathSciNet  Google Scholar 

  30. Nicholls, D.P., Nigam, N.: Exact non-reflecting boundary conditions on general domains. J. Comput. Phys. 194(1), 278–303 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  31. Nicholls, D.P., Nigam, N.: Error analysis of a coupled finite element/DtN map algorithm on general domains. Numer. Math. 105(2), 267–298 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  32. Binford, T.L., Nicholls, D.P., Nigam, N., Warburton, T.: Exact non-reflecting boundary conditions on general domains and hp-finite elements. J. Sci. Comput. 39(2), 265–292 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  33. Strutt, J.W., Rayleigh, L.: On the manufacture and theory of diffraction gratings. Philos. Mag. 47(10), 193–205 (1874)

    Google Scholar 

  34. Bao, G.: Finite element approximation of time harmonic waves in periodic structures. SIAM J. Numer. Anal. 32(4), 1155–1169 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  35. Barnett, A., Greengard, L.: A new integral representation for quasi-periodic fields and its application to two-dimensional band structure calculations. J. Comput. Phys. 229, 6898–6914 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  36. Saad, Y., Schultz, M.H.: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7(3), 856–869 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  37. Nicholls, D.P.: Efficient enforcement of far-field boundary conditions in the transformed field expansions method. J. Comput. Phys. 230(22), 8290–8303 (2011)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This material is based upon work supported in part by the U.S. Department of Energy Office of Science, under Contract Number DE-SC-0001234, and in part by an NSF Grant No. DMS–1115333.

Author information

Authors and Affiliations

  1. Department of Mathematics, University of California, Davis, CA, 95616, USA

    Ying He

  2. Mathematics and Computer Science Division, Argonne National Laboratory, Lemont, IL, 60439, USA

    Misun Min

  3. Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, Chicago, IL, 60607, USA

    David P. Nicholls

Authors
  1. Ying He
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Misun Min
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. David P. Nicholls
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Misun Min.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

He, Y., Min, M. & Nicholls, D.P. A Spectral Element Method with Transparent Boundary Condition for Periodic Layered Media Scattering. J Sci Comput 68, 772–802 (2016). https://doi.org/10.1007/s10915-015-0158-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-015-0158-5

Keywords

Search

Navigation